例析圆题中的“安全隐患”

黑龙江

圆是高中数学的重要组成部分，同时也是高考的高频考点，但在学习本部分内容时，常常会因忽视“安全隐患”而导致解题的失误.现举例加以辨析，以期能对大家解题能力的提升有所帮助.

安全隐患一：忽视必备前提

【例1】若圆C1:x2+y2=1和圆C2:x2+y2-6x-8y-k=0没有公共点，则实数k的取值范围是

( )

A.(-9,11)

B.(-25,-9)

C.(-∞,-9)∪(11,+∞)

D.(-25,-9)∪(11,+∞)

辨析：方程x2+y2+Dx+Ey+F=0能表示圆的前提条件是D2+E2-4F>0，因此若方程x2+y2-6x-8y-k=0能表示圆，则必有(-6)2+(-8)2+4k>0，即k>-25.故选D.

点评：忽视方程x2+y2-6x-8y-k=0能表示圆的必备条件是解此题最大的“隐患”.当然，本题也可借助圆心距与半径的关系：d>r1+r2或0≤d<|r1-r2|来处理.

安全隐患二：遗漏特殊情形

( )

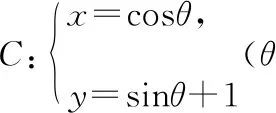
A.相切 B.相交

C.相离 D.相切或相交

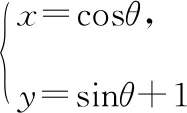
辨析:易知过定点M(1,1)的直线系方程k(x-1)+1-y=0仅不能表示与x轴垂直的直线x=1，而直线x=1恰恰就与圆C相切，因此直线l与圆C始终是相交的，不能相切.故选B.

点评:本题的“安全隐患”藏匿在“特殊情形”之中，不容易被挖掘到，当然该题也可利用圆心到直线的距离d与圆半径r的关系来判断.

安全隐患三：受制隐含条件

( )

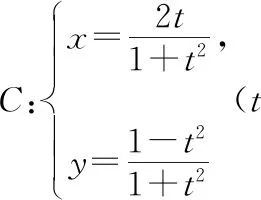
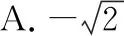
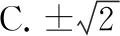
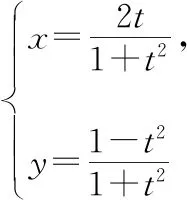
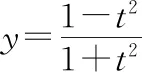
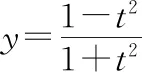
安全隐患四：囿于定式思维

【例4】已知圆C1:x2+y2=1和圆C2:(x-3)2+(y-4)2=4，直线l:3x+4y-11=0，则下列说法正确的是

( )

A.l为两圆的公共弦所在的直线

B.l为两圆的连心线

C.l为两圆的一条公切线

D.l上任一点引两圆的公切线长度相等

错解:将圆C1和C2的方程作差得(x2+y2-1)-[(x-3)2+(y-4)2-4]=0，整理得3x+4y-11=0，即直线l的方程，设两圆的交点为M1(x1,y1)，M2(x2,y2)，易知点M1,M2均在直线l上，故l为C1和C2的公共弦所在的直线.故选A.

点评:该题因思维定式而产生“安全隐患”，误认为两圆C1和C2作差得到的方程永远是两圆公共弦所在的直线方程，而不考虑这两个圆是否相交这一重要前提，应引起注意.

安全隐患五：不是等价转化

( )

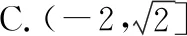
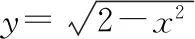
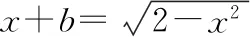
点评：在进行平方运算时，最大的“隐患”在于忽视了“等价性”，当然处理本题最好的方法是借助数形结合，可以成功绕过“危险地带”.

安全隐患六：丢掉变量范围

【例6】若圆C:x2+(y-a)2=1与抛物线P:x2=2y有公共点，则实数a的取值范围是

( )

A.(-∞,1] B.[-1,1]

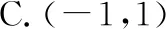
错解:将x2=2y代入圆C的方程并消去x整理得y2+(2-2a)y+a2-1=0(*)，依题意有Δ=(2-2a)2-4(a2-1)≥0，解得a≤1.故选A.

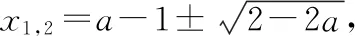
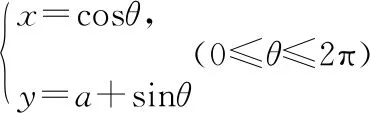
安全隐患七：错用圆系方程

【例7】经过圆C1：(x-1)2+(y-2)2=1和圆C2：x2+y2=4的交点，且和直线l：3x+4y-10=0相切的圆方程为

( )

A.x2+y2+10x+20y-44=0

B.x2+y2=4

C.x2+y2=4或x2+y2+10x+20y-44=0

D.非上述答案

错解:设所求圆的方程为C:(x-1)2+(y-2)2-1+λ(x2+y2-4)=0(λ≠-1),

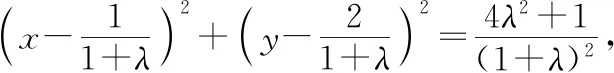
辨析:本题错在所设的圆系方程(x-1)2+(y-2)2-1+λ(x2+y2-4)=0不能表示圆x2+y2=4，而圆x2+y2=4恰好也满足条件.

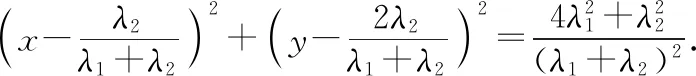
点评:利用曲线系方程解题往往能给我们带来方便，但有时也可能会因忽视限制条件而产生“安全隐患”，解题时要做到扬长避短.

安全隐患八：方法选择不当

( )

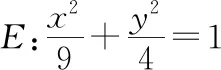
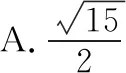
C.4 D.2或4

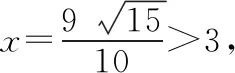
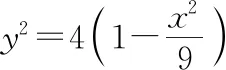
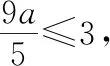
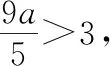
综合(1)和(2)可知选D.

点评：上述解题的“隐患”在于忽视了用判别式法解决某些二次曲线的交点问题是失效的！到底应采用怎样的方法还需依据题目的特点，具体问题具体分析.