平底锥柱型药柱燃烧规律研究*

杨艳羽，相升海，刘瑞东，闫利伟，于 兵

(1 沈阳理工大学装备工程学院，沈阳 110159；2 辽宁北方华丰特种化工有限公司，辽宁抚顺 113003 )

0 引言

固体火箭发动机的装药燃烧规律在很大程度上决定了发动机内弹道性能[1]。锥柱型药柱是一种三维药柱，其燃面可调范围大、结构完整性好、体积装填系数高[2]。文献[3]研究了翼柱型药柱的参数设计和燃烧面积变化过程。文献[4]给出了开槽管型药柱的燃面计算公式。文献[5]分析了星孔型药柱、车轮型药柱、套管型药柱和短管型药柱的减面性。综上所述，与锥柱型药柱燃烧规律相关的公开发表的文献较少。文中主要是对平底锥柱型药柱燃烧规律进行研究。

1 平底锥柱型药柱

按照封头种类的不同，锥柱型药柱可分为平底锥柱型药柱、椭球形锥柱型药柱和蝶形锥柱型药柱等。文中研究的是将前端面和外表面包覆后的平底锥柱型药柱。

如图1所示，平底锥柱型的主要几何参数有：外径D，长度L，前圆柱段长L1，前圆柱段内孔半径R1，圆柱段长L2，圆柱段内孔半径R2，环向槽圆弧半径r，环向槽圆弧圆心旋转半径R3，环向槽锥面倾角α1和α2(文中的倾角参数采用弧度单位，长度参数采用以外径为基准的无量纲单位)。

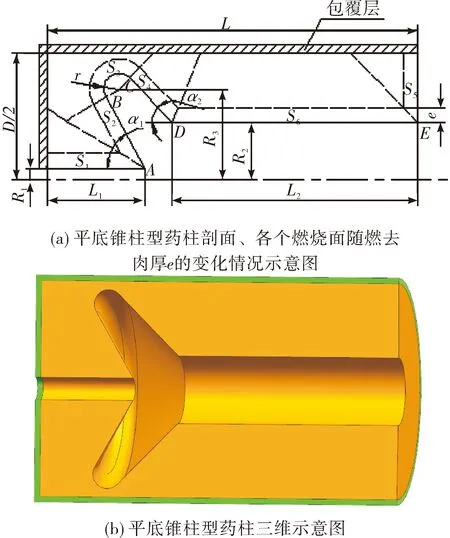
图1 平底锥柱型药柱示意图

2 理论基础

2.1 几何燃烧规律

文中采用几何燃烧规律，它包括3个基本假定：

1)整个装药的燃烧表面同时点燃；

2)装药成分均匀，燃烧表面各点的条件相同；

3)燃烧表面上各点都以相同的燃速向装药里面推移。

2.2 3个基本型的侧面积公式

根据药柱的几何形状和燃烧规律，可将其划分为直柱体、圆台和曲线弧绕坐标轴旋转所得旋转体3种基本类型。

1)曲线弧绕坐标轴旋转所得旋转体的侧面积

定理 设函数f(x)在区间[a,b]上非负可导，对由曲线弧y=f(x)，直线x=a，x=b与x轴所围成的曲边梯形，绕x轴旋转一周所生成旋转体的侧面积为S[6]。

(1)

2)直柱体的侧面积

计算直柱体侧面积公式为：

S=Ch

(2)

其中:C为底面周长;h为直柱体的高。

3)圆台的侧面积

设圆台的上、下底面半径分别为r1、r2，母线长为l，则其侧面积为：

S=π(r1+r2)l

(3)

3 燃烧规律研究

3.1 燃面计算

根据3个基本型公式，推导出各个燃烧面积公式，其中各个燃烧面积的位置参见图1(a)。

1)前圆柱段面S1

(4)

2)环向槽前锥面S2

(5)

3)环向槽圆弧面S3

S3=2π[R3+(r+e)(sinα1+sinα2)/

(π-α1+α2)](r+e)(π-α1+α2)

(6)

4)环向槽后锥面S4

(7)

5)后圆柱面S5

(8)

6)后端面S6

(9)

综上可得，平底锥柱型药柱总燃烧面积S为：

(10)

3.2 长径比对燃面变化规律的影响

为了找到更接近恒面燃烧的药柱参数，选取了5组长径比不同的药柱进行研究(见图2)。对比图2中的5条曲线可以发现：药柱都具有先增面性后减面性的燃烧规律，但当长径比为2.5时，曲线相对平缓，更接近恒面燃烧。因此，将选取长径比为2.5的药柱进一步研究其燃烧规律。

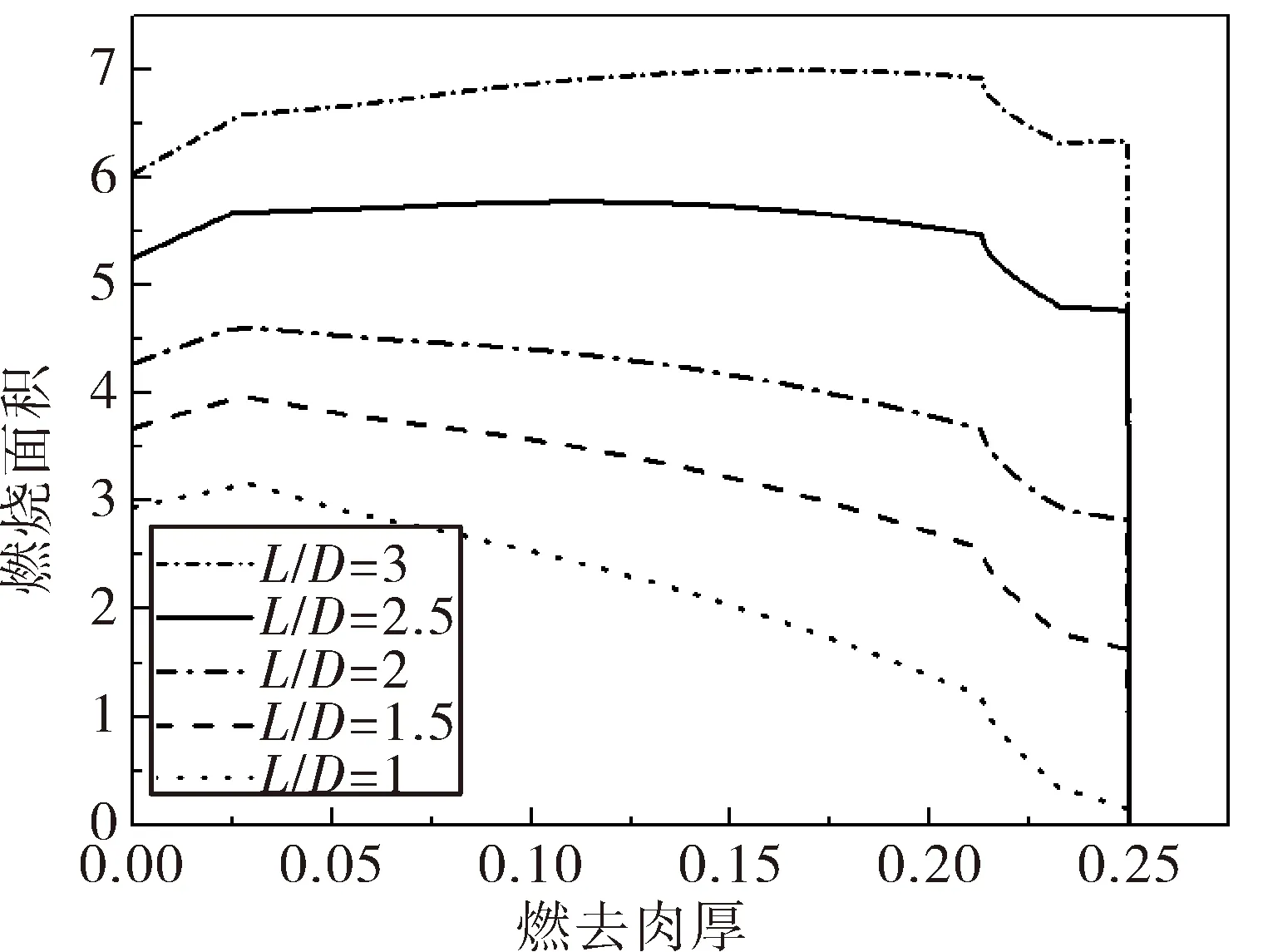
图2 不同长径比的药柱燃面随燃去肉厚e变化曲线

3.3 燃烧过程中关键点的确定

在整个燃烧过程中共有7个关键点(见图3)。

图3 燃烧过程中的关键点

1)环向槽圆弧分裂点e1

(11)

2)环向槽圆弧右段消失点e2

由(e2+r)cosα2=r+e1可得:

e2=(r+e1)/cosα2-r

(12)

3)环向槽前锥面消失点e3

由R1+e3=R3-(r+e3)cosα1得:

(13)

4)环向槽左段分裂点e4

(14)

5)环向槽燃完点e5

由(r+e5)2=(r+e4)2+(D/2-R3)2得：

(15)

6)前圆柱段燃完点e6

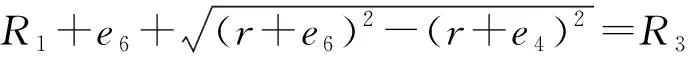
(16)

7)药柱完全燃完点e7

(17)

3.4 约束条件

为了寻求近似恒面燃烧条件下的最优药型参数，以关键点相等为约束条件，使其对应燃面同时消失。

令e3=e6得：

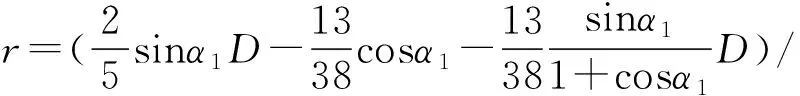
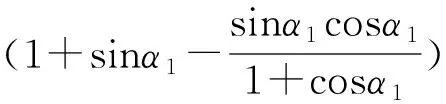
(18)

令e7=e3得：

(19)

令e1=e3得：

(20)

3.5 燃烧规律

燃烧面积对燃去肉厚求导得：

2π(cscα1+cscα2+sinα1+sinα2)r+

2π[(π-α1+α2)+(cotα2-cotα1)]R3-

(21)

令：

A2=2π(cscα1+cscα2+sinα1+sinα2)

A3=2π[(π-α1+α2)+(cotα2-cotα1)]

其中A1与α1、α2的变化关系见图4。

则：

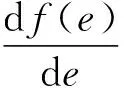
(22)

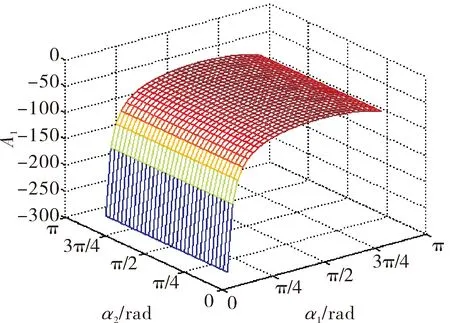
图4 A1与α1、α2的变化关系

由图4可见，在α1∈(0,π)，α2∈(0,π)的区间内，A1取值恒小于零，即A1恒为0不成立，因此平底锥柱型药柱不存在恒面燃烧。

2)敏感度分析

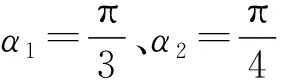
图5 设计变量对的影响图

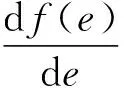
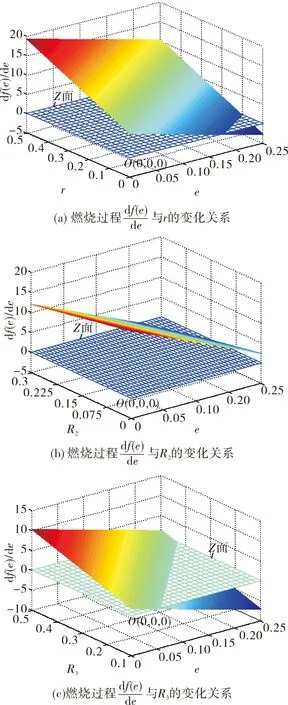
图6 燃烧过程与r、R2、R3的关系

图6表明：

3.6 燃通比与药柱内孔半径的关系

燃通比为：

(23)

式中：Si为药柱内孔的燃烧面积；Api为药柱内孔的通气面积[1]。

以药柱外径为基准，圆柱内孔相对半径R2在0.025至0.25之间变化时，燃通比对圆柱内孔半径的影响曲线图见图7。当圆柱内孔相对半径小于0.075时，燃通比大于100，容易引起爆轰，因此选用的圆柱内孔相对半径大于0.075。

图7 燃通比与圆柱内孔半径的变化曲线

4 算例

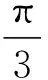
运用UG软件对长径比为2.5的平底锥柱型药柱进行建模，选择5个关键点提取其对应的燃烧面积与公式计算求得的燃烧面积数据进行对比。如表1所示，公式计算得出的数据与实际数据的最大相对误差为0.17%，证明了公式的正确性。

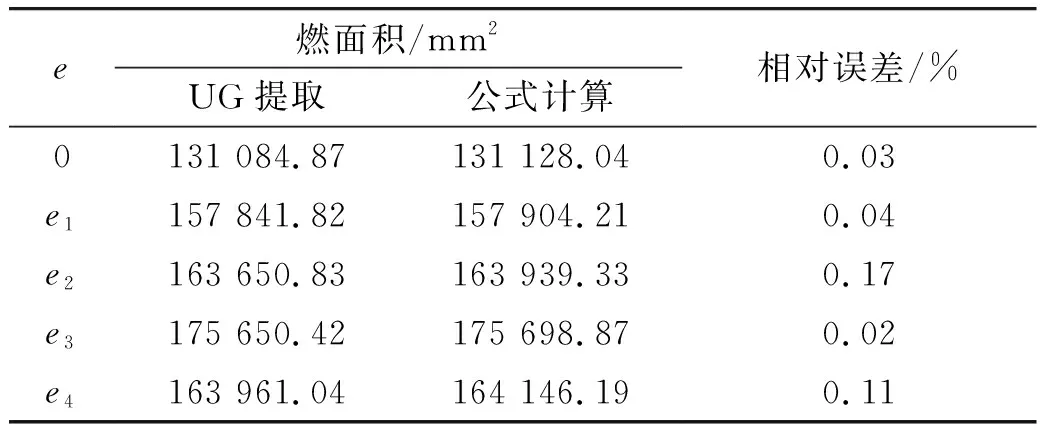
表1 计算燃面积与UG提取燃面积数据对比

以药柱外径为基准，得到环向槽圆弧相对半径r为0.068，圆柱段内孔相对半径R2为0.25，环向槽圆弧圆心旋转相对半径R3为0.395。根据图6给出的关系图，燃烧药柱应该呈现先增面性后减面性。

根据式(4)～式(10)，得到燃烧面积随燃去肉厚的变化曲线见图8。从图8中可以看出，燃烧药柱呈现先增面性后减面性，与得出的燃烧规律吻合。

图8 燃面随燃去肉厚e变化曲线

5 结论

1)长径比为2.5时，更接近恒面燃烧。

2)由于燃通比的限制，圆柱内孔相对半径R2大于0.075。

3)以药柱外径为基准，当环向槽圆弧相对半径r∈(0，0.1)，圆柱段内孔相对半径R2∈(0.09，0.3)，环向槽圆弧圆心旋转相对半径R3∈(R2，0.44)，燃烧药柱呈现先增面性后减面性。

4)平底锥柱型药柱不存在恒面燃烧。