浅谈桥式起重机载荷形状对摆动的影响

刘泽阳，王涌

（中交第二航务工程局有限公司第六工程分公司，湖北 武汉 430060）

1 系统模型

载荷摆动因自身的惯性导致，可以设想一个运行中的桥式起重机：在发生制动时，桥式起重机减速，而载荷将继续向前拉拽起重机。在起重机停止后，载荷将继续像钟摆一样摆动。摆动的时长取决于起重机绳长和载荷重心（G.G）到装置悬挂点的距离。除了上述距离外，载荷形状也有可能对载荷偏转和摆动产生影响。

1.1 系统模型描述

本系统模拟桥式起重机做功时运动状况，假设起重机电动葫芦钢丝绳到载荷之间距离不变，在给定条件下，设计系统具有3个自由度，即3个广义坐标系：（1）x为起重机的运动轨迹；（2）φ为中垂线与钢丝绳之间的夹角；（3）ψ为中垂线与摆动试验载荷之间的夹角。

系统中起重机行进过程中传动部件的动态力矩较小，计算中可忽略。起重机放置在钢筋场密闭空间下，可看作理想化无风状态，因此风阻力未被纳入考虑范围。通过研究电动起重机启动阶段状态，分析载荷形状对载荷摆动的影响。

如图1所示，系统中质量为m2（kg）的电动起重机，下端悬挂着长度为l（m）的钢丝绳。且起重机使用钢丝绳保持绝对刚性，忽略其弹性形变量。在钢丝绳一端，吊装了1个质量为m（kg）试验载荷。电动起重机由1台启动力矩为M（N·m）的齿轮电机驱动，其转动惯量为IM（kg·m2）。电机与行走轮之间的传动比例为i。电动起重机有4个行走轮，每个轮子的惯性矩为I3（kg·m2），半径为r（m）。从载荷重心到装置悬挂点的距离为rs（m）。

1.2 起重机选择

对桥式起重机运动状态进行模拟时，首先需确定起重机类型和主要性能参数。如额定起重量Q、小车行进速度Vp、自重等。模型采集电动起重机详细参数如下：负载能力Q为500kg；行进电机功率Pp为0.1kW；传动部分惯性矩IM为0.0007kg·m2；主电机额定转速nM为820min-1；电机的启动力矩M为1.863N·m；行进速度vp为20m·min-1；行进轮半径r为0.06m；行进轮的惯性矩I3为0.007859kg·m2；比例i为15.457；质量m2为163kg。

2 载荷形状对其摆动的影响

2.1 载荷选择

转动惯量是刚体绕轴转动时惯性（回转物体保持其匀速圆周运动或静止的特性）的量，在选择试验载荷时出于便于载荷转动惯量I（kg·m2）计算的考虑，载荷体选择两种形状不同的规则几何体，同时其质量必须均匀分布。模拟桥式起重机实际使用中的常见载荷形状，选择使用长方体和圆柱体作为试验载荷。

（1）载荷A模型。载荷A选择1个质量均匀分布的长方体，取值质量mA=29kg，长方体外形尺寸如图1所示。

（2）载荷B模型。载荷B选择1个质量均匀分布的圆柱体，取值质量mB=30kg，圆柱体外形尺寸如图2所示。

图1 载荷A模型

图2 载荷B模型

2.2 转动惯量求解

2.2.1 载荷A转动惯量

载荷A的质量=29kg。如上所述，对于规则的几何形状来说，转动惯量计算方式简单。可由式（1）导出。

围绕载荷A的S轴，关于尺寸w1（m）、w2（m）的计算方案见图3。

2.2.2 载荷B转动惯量

圆柱体载荷B在启动阶段不会绕着自身的旋转轴发生转动，而是围绕垂直于圆柱体旋转轴的轴旋转，如图4所示。根据式（2）得出该圆柱体载荷的转动惯量。

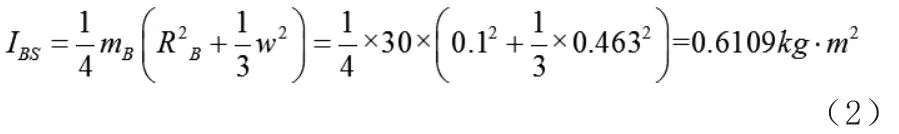
载荷A与载荷B的质量相同形状不同，其转动惯量却完全不同。载荷B的转动惯量IBS（kg·m2）几乎是载荷A转动惯量IAS（kg·m2）的3倍。

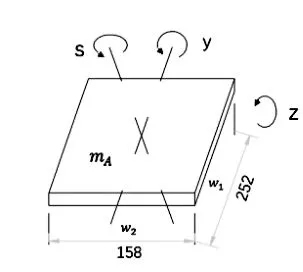
图3 载荷A的转动惯量计算方案

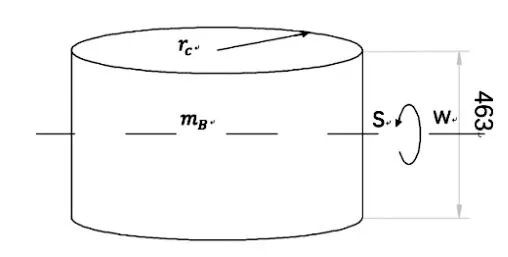
图4 载荷B的转动惯量计算方案

3 验证分析

3.1 条件

载荷A与载荷B参数对比见表1。

表1 载荷对比

3.2 行进阻力求解

桥式起重机的行进轮的阻力可通过式（3）来确定。

式（3） 中：e为 滚 动 摩 擦，m，e=0.0007m；fc为轴承摩擦系数，fc=0.1；rp为行进轮固定销的直径，m，rp=0.011m；χ为额外阻力，χ=2.5。

且在代入式（3）后，得出载荷A和载荷B的行进阻力值，见式（4）和式（5）。

3.3 线性质量惯性力求解

惯性力又称为虚拟力，作用于行进轮的边缘，可通过式（6）计算。

式（6）中：tr为电机的启动时间，s，tr=0.7s。

代入式（6）后，得到载荷A和载荷B的惯性力值，见式（7）和式（8）。

3.4 力矩方程式求解

电机的实际传动力矩Mr（N·m）必须大于启动力矩推导出来的原因力矩总和。该合力值可通过力矩方程式得出：

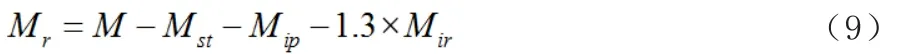
代入（9）后，得到式（10）和式（11）。

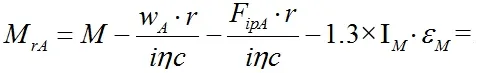
式（10）和式（11）中：Mst为被动阻力的力矩，N·m；Mip为线性质量的惯性矩，N·m；η为电动起重机的行进单元总效率；εM为电机轴的角加速度，s-2。

3.5 理论结果

如上所述，运动方程式以拉格朗日力学为原理推导而出，对这些方程式进行求解，具体如式（12）～（14）所示。

通过积分得出x˙、φ˙、ψ˙，单位均为m·s-1。再一次积分得出x（m）、φ（deg）、ψ（deg）。在近似数值求解的基础上，得出上述值的理论结果，见表2。

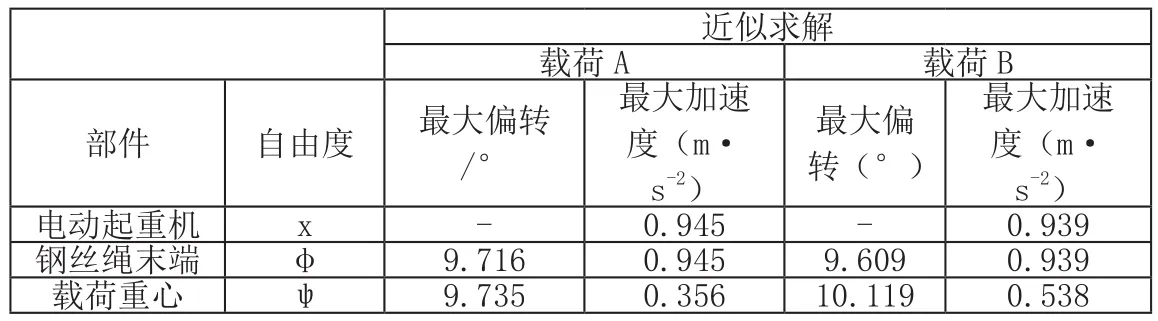
表2 理论结果

从表2得知：很明显转动惯量Is（kg·m2）越大，对钢丝绳加速度的影响就越明显。另外载荷的转动惯性Is（kg·m2）与距离rs（m）越大，载荷重心加速度就越大。因此，载荷形状能够明显影响载荷及钢丝绳末端摆动。

4 结语

综上所述，在载荷质量大致相等情况下，载荷形状对载荷加速度及发生偏转摆动都存在显著影响，转动惯量越大，载荷加速度越大，其也偏转角也越大。在桥式起重机吊装作业时应充分考虑载荷绑扎形状，能有效地抑制桥式起重机载荷摆动，保证起重机稳、准、快地安全生产，减少桥式起重机事故的发生，提高桥式起重机的工作效率、安全性和可靠性。