缩减法计算刚体的转动惯量

田斯绮 贺西平

(陕西师范大学物理学与信息技术学院，陕西 西安 710062)

惯性描述的是物体对其运动状态变化的一种阻碍程度。当作用在物体上的外力为零时，物体将保持其运动状态不变，即维持静止或匀速直线运动。除了物体作平动时表现出惯性外，物体以某一角速度绕某轴转动时也会表现出转动惯性，我们通常用转动惯量来衡量物体转动时的惯性大小。其量值取决于物体的形状、质量分布及转轴的位置。

任何刚体的转动惯量都可以通过实验方法(如扭摆法)、微元模型法、质量投影法等得到[1-4]。对于规则形状的刚体，在大学物理课本中是通过微积分方法计算得到。文献[5]介绍了一种用缩减法计算刚体转动惯量的方法，可看作是计算转动惯量的一种扩展方法。缩减法的基本思想是，针对对称性刚体，即按比例放大或缩小原刚体，引入无量纲常数并保持转动惯量的量纲不变，求得该无量纲常数进而得到转动惯量。本文阐述了这种方法的原理并将该方法加以推广，应用于实际中常见的二维及三维对称刚体的转动惯量计算中[6]，这对于已经学过微积分的大一学生来说，有利于开阔他们的思路，更进一步理解转动惯量的物理意义，并掌握计算转动惯量的方法。

1 缩减法

缩减法的实质是基于方程两端物理量的量纲相同。转动惯量的量纲是ML2。例如，若质量为M的二维物体具有由x和y给出的独立长度，则其转动惯量可能是由Mx2,My2,Mxy,Mx-1y3,Mx1/2y3/2等项组成的多项式，每项的量纲都应与转动惯量的量纲相同。

因此，根据转动惯量的量纲，引入无量纲常数后，具有一个独立长度的一维物体的转动惯量可以表示为

I=kMl2

(1)

M是物体的质量，l是物体的独立长度，k是待定的无量纲常数。

同理，二维物体的转动惯量则可表示为

(2)

M是物体的质量，l1、l2是物体的两个独立长度，{kx}是待定的无量纲常数。

同上之理，三维物体的转动惯量可以表示为

(3)

M是物体的质量，l1、l2、l3是物体的3个独立长度，{kx,y}是待定的无量纲常数。

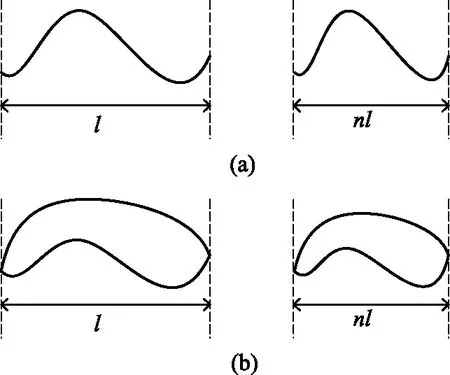
图1 按比例缩放物体

分析式(1)可知，如果均匀密度的一维物体成比例地收缩或按比例扩大，如图1(a)所示，则缩放后物体的转动惯量可由下式给出

(4)

其中，n是线性比例因子(缩放倍数)；I′为缩放后刚体的转动惯量。

如果均匀密度的二维物体按比例收缩或按比例放大，如图1(b)所示，则物体的转动惯量可由下式给出

(5)

如果均匀密度的三维物体按比例收缩或按比例放大，则所得物体的转动惯量可由下式给出

(6)

缩放后所产生的新刚体与原始刚体形状相似。结合平行轴定理，基于量纲分析就可计算出无量纲常数，进而求出原始刚体的转动惯量，这种方法就是缩减法。

2 算例

2.1 等腰三角形的转动惯量

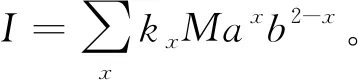
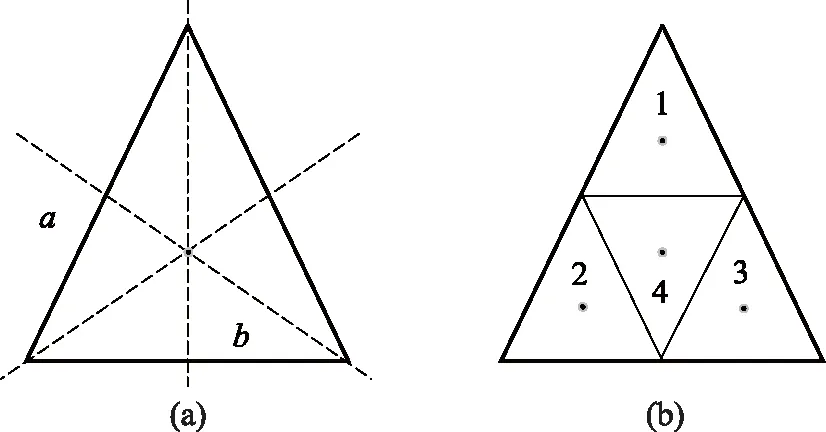
图2 计算等腰三角形的转动惯量

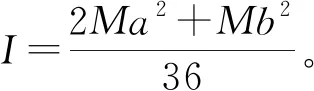
2.2 矩形的转动惯量

2.2.1 轴线为过质心且与对称轴夹角为θ

质量为M、长为a、宽为b的实心矩形绕过其质心所在平面(x-y平面)的轴线旋转，且该轴线与y轴夹角为θ，如图3(a)所示。

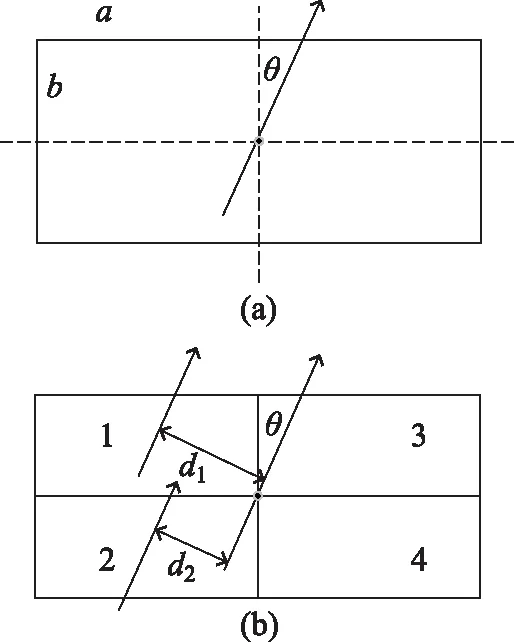
图3 计算矩形的转动惯量

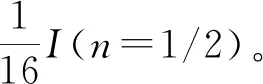
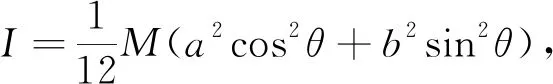
2.2.2 轴线为垂直穿过其质心

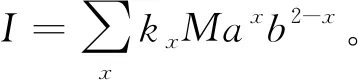
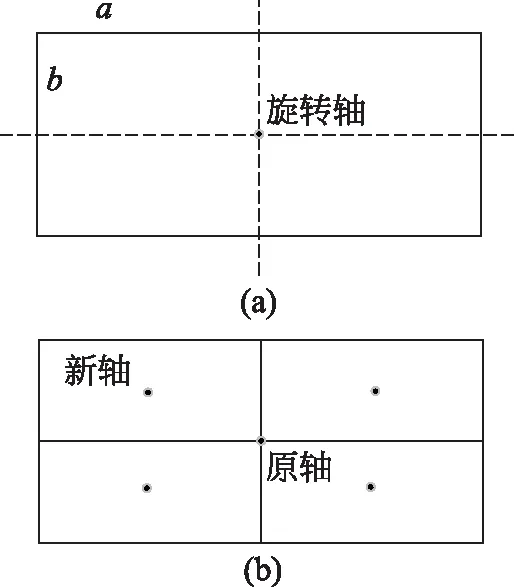
图4 计算矩形的转动惯量

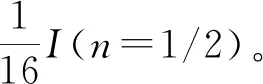
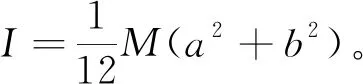
2.3 长方体的转动惯量

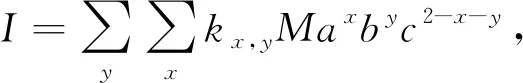
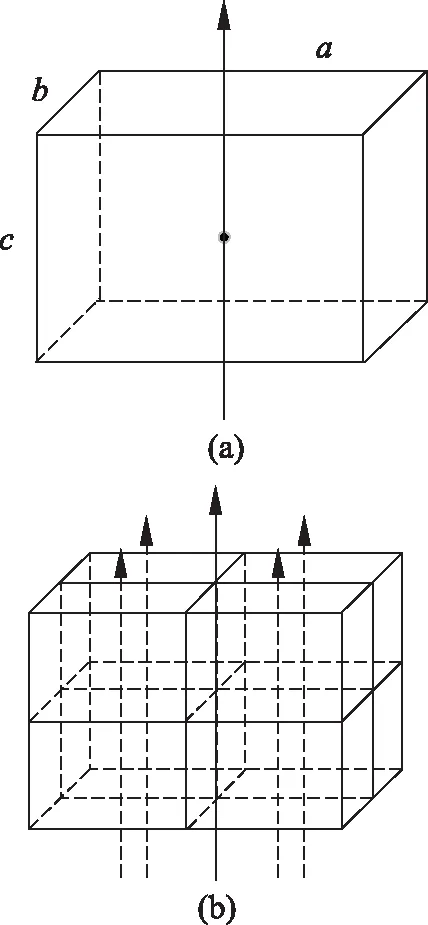
图5 计算长方体的转动惯量

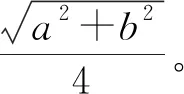
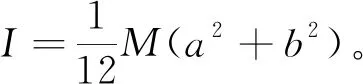
4 结语

本文阐述了缩减法计算对称刚体转动惯量的思想，即按比例放大或缩小原刚体，引入无量纲常数并保持转动惯量的量纲不变，结合平行轴定理，可求得该无量纲常数进而得到转动惯量。文中提供了等腰三角形、矩形等4个算例。缩减法计算刚体的转动惯量有利于学生更易于理解转动惯量的物理意义。