考虑空穴效应的球面轴承性能研究

2019-07-25李争陈晴王群京

轴承 2019年9期

李争，陈晴，王群京

(1.河北科技大学电气工程学院,石家庄 050018；2.安徽大学高节能电机及控制技术国家地方联合工程实验室，合肥 230601)

流体动压球面轴承是旋转机械的主要支承部件，因结构简单，正常工作时无结构件接触摩擦，能耗低等原因广泛应用于液质悬浮多自由度永磁电动机，推进了多自由度运动装置朝着高效环保和高精度定位的方向发展。传统的多自由度电动机采用机械装置连接，结构复杂，摩擦磨损严重，效率低且可靠性差。液质悬浮多自由度永磁电动机采用球面轴承润滑支承结构，定子和转子间隙充满润滑油，使其表面无直接接触，通过楔形效应产生的油膜压力支承载荷，实现了高精度定位，灵活驱动，无接触摩擦运行，保证了多自由度永磁电动机的可靠运行，在机器人、航空航天、船舶动力系统等高精度定位的控制领域具有广泛的应用前景[1-4]。

润滑剂性能直接影响电动机的寿命，随着流体动压球面轴承在多自由度电动机中的广泛应用，为了使其能够长期稳定高效地工作，考虑到轴承中的一部分润滑油发生相变，成为油蒸气，形成空穴效应会加速磨损，降低使用寿命，增加噪声，因此有必要对球面轴承油膜中的气穴进行研究。研究人员对计入空化效应的轴承性能进行了计算分析[5-8]，文献[9]基于转子-轴承系统的物理模型，提出一种计算流体动力与流固耦合相结合的瞬态分析方法，研究了热影响和空穴效应，并与试验结果进行比较，验证了理论预测的正确性；文献[10]模拟了有无考虑气穴影响时椭圆滑动轴承的压力分布情况，并分析了考虑气穴影响时轴承在不同轴颈转速和供油压力下压力场的分布规律；文献[11]采用混合模型对滑动轴承的气穴现象进行建模，对弹性变形引起的流场进行修正，基于多目标遗传算法对2个耦合系统进行设计优化；文献[12]运用 FLUENT 两相流模型并考虑空穴效应，分析三油槽滑动轴承湍流状态下的油膜，得到不同进油压力和润滑油黏度对油膜承载力和气穴的影响；文献[13]采用有限体积法对两相流及自然空化模型进行数值分析，得到不同油膜压力分布及转速下空穴区气相体积分数分布。

以上文献都是对滑动轴承的空穴现象进行分析，缺少对用于多自由度电动机这类装置的球面轴承空穴现象的深入研究，又鉴于传统的流体动压滑动轴承分析方法通常应用基于Navier-Stokes方程和连续性方程导出的Reynolds方程的有限差分法，虽可获得所需的基本数据，但其润滑理论中的基本假设限制了湍流、热传递和气穴现象等复杂流动的建模和模拟。因此，现基于有限元多物理场耦合平台，分析考虑空穴效应时球面轴承的压力和形变。

1 原理分析

液质悬浮多自由度永磁电动机(图1)主要由球面轴承和电磁结构组成，球面轴承的中空转子壳嵌在非完整球面的定子壳内，转子壳在赤道和尾部位置分别固定着交替排列的N和S极贴片式永磁体和圆盘状永磁体，在定子壳外围安装有爪形空心圆柱线圈组，通过改变和组合不同方位定子线圈的通电方式，配合永磁体产生不同方位的电磁力，驱动转子完成多自由度运动。

图1 液质悬浮多自由度永磁球面电动机示意图

电动机工作中，通电线圈电生磁和永磁体相互作用的电磁力驱动转子壳转动，由于定子壳外球面直径大于转子壳内球面直径，所以二者存在偏心，两球面间存在不相等的间隙，形成收敛区和发散区。转子壳在定子壳中转动时把邻近的润滑油带入收敛的楔形间隙，润滑油受到挤压产生抵抗力，即油膜的动压承载力，将定子壳与转子壳分离，并承受外载荷，使摩擦副为纯液体润滑[15]，球面转子的旋转模型如图2所示。图中，O1为转子壳中心；O为定子壳中心；e1=OO″和e2=O1O″分别为二者间的周向和轴向偏心距。在发散区部分油膜由于压力低于润滑油的饱和蒸气压，流体转化为蒸气，油蒸气将填充发散区域，出现空穴，改变流场的状态，使得油膜自然破裂。

图2 动态球面转子在液体中的旋转模型

2 数学理论

2.1 流体流动方程

考虑空穴现象，球面轴承发散区的油膜会因承受太大负压而自然破裂，润滑油气化[10]，从而形成气液两相流，而两相流流动情况不但要遵循连续性方程、运动方程等基本的物理守恒定律，还要遵循组分质量守恒定律[14-16]。

2.1.1 连续性方程

流体动压滑动轴承的压力分布受Reynolds方程控制，该方程由Navier-Stokes连续性方程和动量方程导出。这些方程是针对适用于所有类型流动的质量和动量进行求解的,可压缩流和不可压缩流的一般质量守恒方程为[16]

(1)

式中：ρm为气液混合流体密度；kg/m3；vm为混合流体速度，m/s；k为相数，k=1为液体，k=2为气体；α为体积分数；t为时间，s。

2.1.2 运动方程

由动量定理得到运动方程为[10]

(2)

式中:p为静压，Pa ；τ为应力张量；g为重力加速度；F为外力，N；μm为混合流体黏度，Pa·s；υdk为气相滑移速度，m/s。

2.1.3 组分质量守恒方程

动压油膜球面轴承因出现空穴现象，计算域流场的介质发生变化，由单相流变成了多相流，物质的传输转换在组分质量守恒定律的控制方程下完成[10]，即

(3)

式中：m12(21)为液气(气液)质量转换速度。

2.2 流体结构相互作用方程

流体润滑油与定子壳相互影响，润滑油在定子壳上施加压力，导致定子壳变形，从而改变流动区域[11]，利用有限元多物理场耦合仿真平台对定子壳进行变形分析，控制方程为

(4)

(5)

式中：Ms为结构质量矩阵；Mf为流体质量矩阵；Fs和Ff分别为结构和流体力矩阵；R为有效表面积的耦合矩阵，与流体结构界面中的每个节点相关联；Ks为固体域的刚度矩阵；Kf为流体域的刚度矩阵；U为固体形变量；P为流体压力。

2.3 球面轴承油膜厚度方程

流固界面在流体域的相对位移与固体域的相对位移一致，润滑油膜厚度定义为转子球壳-润滑油界面和定子球壳-润滑油界面之间的距离，即

h=C(1+ε1sinθcosφ+ε2cosθ)，

(6)

3 仿真分析

球面轴承的结构尺寸及模型参数见表1。模型包括转子壳、定子壳及润滑膜，润滑油选择轻质润滑油，假设是不可压缩的，转子壳以15.7 rad/s的角速度运转，定转子壳采用尼龙材料，假设球壳厚度均匀，定子、转子间密封一层润滑油，定子壳外表面设为固定边界约束条件，将油膜层外表面与定子壳内表面设置为流固耦合面，计算时先求解润滑油流场，得到流体润滑油压力作为定子壳内表面的边界载荷，将压力传递到固体力学分析模块，得到定子球壳的变形情况，完成耦合面流场压力与固体变形的转化。

表1 球面轴承的结构尺寸及模型参数

空化模型选用COMSOL Multiphysics 软件的“流体流动”模块下的“薄膜流动，壳”物理场，利用其中的“空化”接口确定润滑油压力和质量分数，有助于预测轴承的润滑层中气体空穴的形成和发展。添加表1的边界条件对模型进行网格划分，考虑到网格质量对有限元计算的精度和计算效率有直接影响，模型采用物理场控制网格序列类型，利用三角形网格单元将油膜区域离散化，单元大小较细化，其中在模型的进油孔区域网格划分较为密集。球面轴承的耦合系统网格划分如图3所示，由于最小油膜处的厚度较小，又是分析重点，网格数过少会降低网格质量，增大误差，网格数过大将增加计算的时间，经计算，网格总数为267 501可保证短时间高精度计算。最后，采用MUMPS直接线性求解器进行稳态求解。

图3 球面轴承的耦合系统网格模型

4 试验

试验系统简图如图4所示。转子球壳密封在定子球壳内，定子球壳由2个定子半球壳组成，半球壳间设有密封圈，保证装置密封效果良好。借助于变频电动机驱动球面转子运转，由变频器为电动机提供不同频率的驱动电压，使其与转子以不同转速工作，压力传感器安装在球面轴承的定子外壳上，用于测量加载区域中的油膜压力，压力传感器输出的电压信号连接到数据采集系统进行记录和处理，使用多点指示器开关更改位置。试验角速度为5.6～31.4 rad/s，由变频器设定。允许系统在30 min内达到稳定状态，并测量相应的压力，每个角速度取3组读数，取其平均值用于分析。

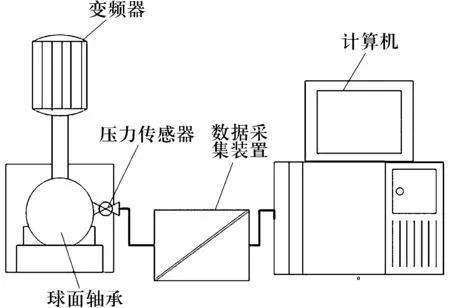
图4 油膜压力试验系统简图

5 结果与分析

5.1 空穴效应

有无考虑空穴效应时油膜压力分布如图5所示。由图可知，不考虑空穴效应时，油膜承载区最高压力为1 MPa，发散区与收敛区的压力相等但为负值(图5a)，负压并不能在实际流体中发生，负压下油膜必然遭到破坏而出现空穴现象，从而形成两相流；考虑空穴效应时只存在收敛区的正压力，由于负压已消失，峰值压力变为0.9 MPa(图5b)。理论上液体润滑油是不能承受负压的，不符合实际情况，所以考虑空穴效应时的计算结果更为合理。

图5 球面轴承油膜压力分布

有无考虑空穴效应时赤道处周向压力分布如图6所示。由图可知，不考虑空穴效应时轴承的峰值压力大于考虑空穴效应时的，这也证明了空穴效应会降低正压力峰值。

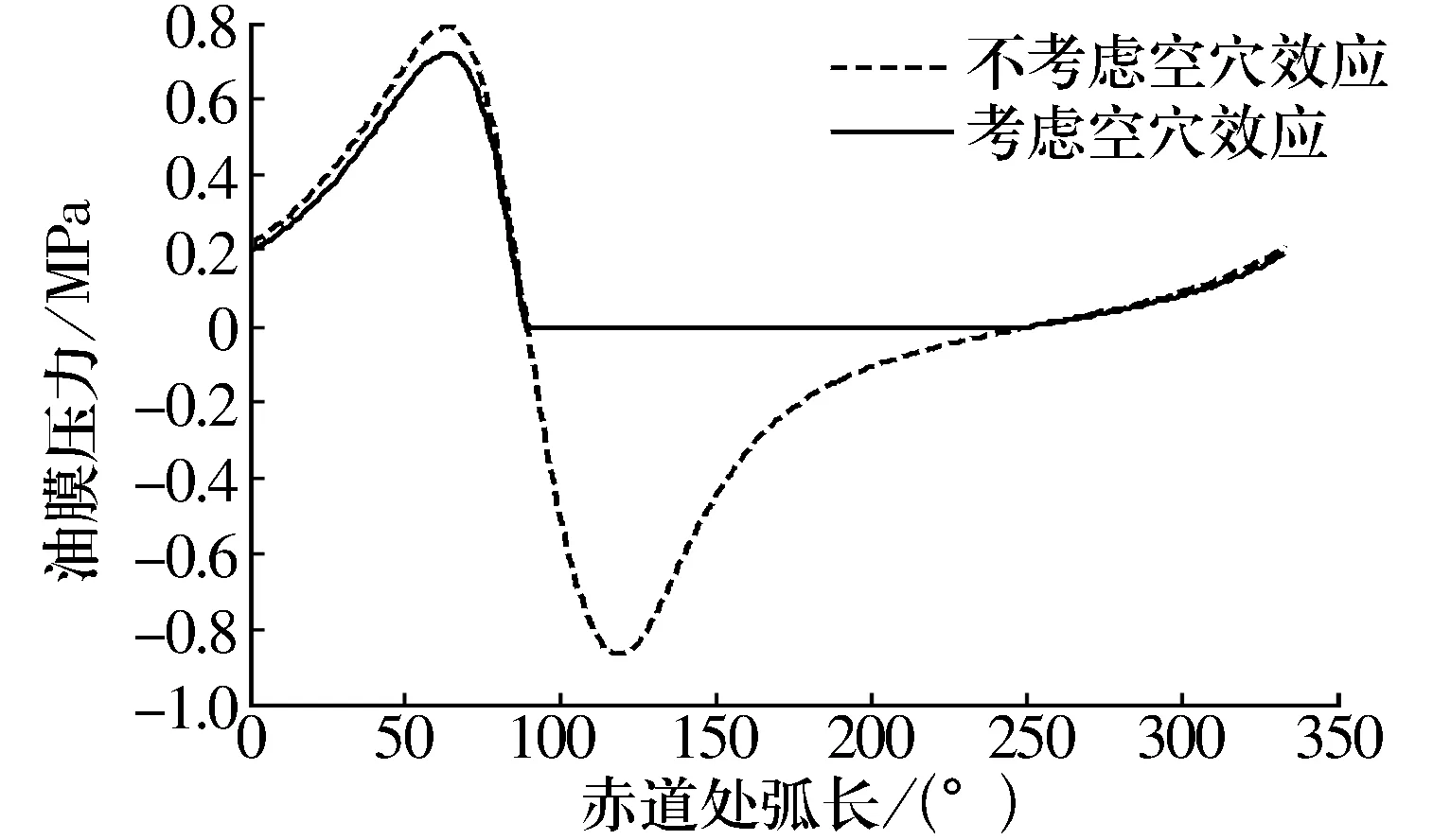
图6 赤道处油膜压力分布

5.2 流固耦合

油膜空穴效应不仅能反映球面轴承内润滑油膜运动的连续性和流动性，还能反映转子壳转动时油膜与定子壳流固耦合关系。流体与固体耦合时，主要体现在固体结构的应力和位移变化。有无考虑空穴效应时油膜对定子壳的应力及形变如图7所示。由图可知，2种情况下定子壳均发生了凸起的形变，而球壳形变会引起定子和转子间的间隙和偏心率变化，从而改变润滑油的流动状态，使油膜压力也发生变化，进而改变定子壳的形变，因此形成一个双向流固耦合。考虑空穴效应的定子壳形变只发生在收敛区，且定子壳的应力小于不考虑空穴效应时的，这是由于定子壳应力分布取决于油膜压力的分布和梯度变化，而考虑空穴效应时油膜压力相对小一些。

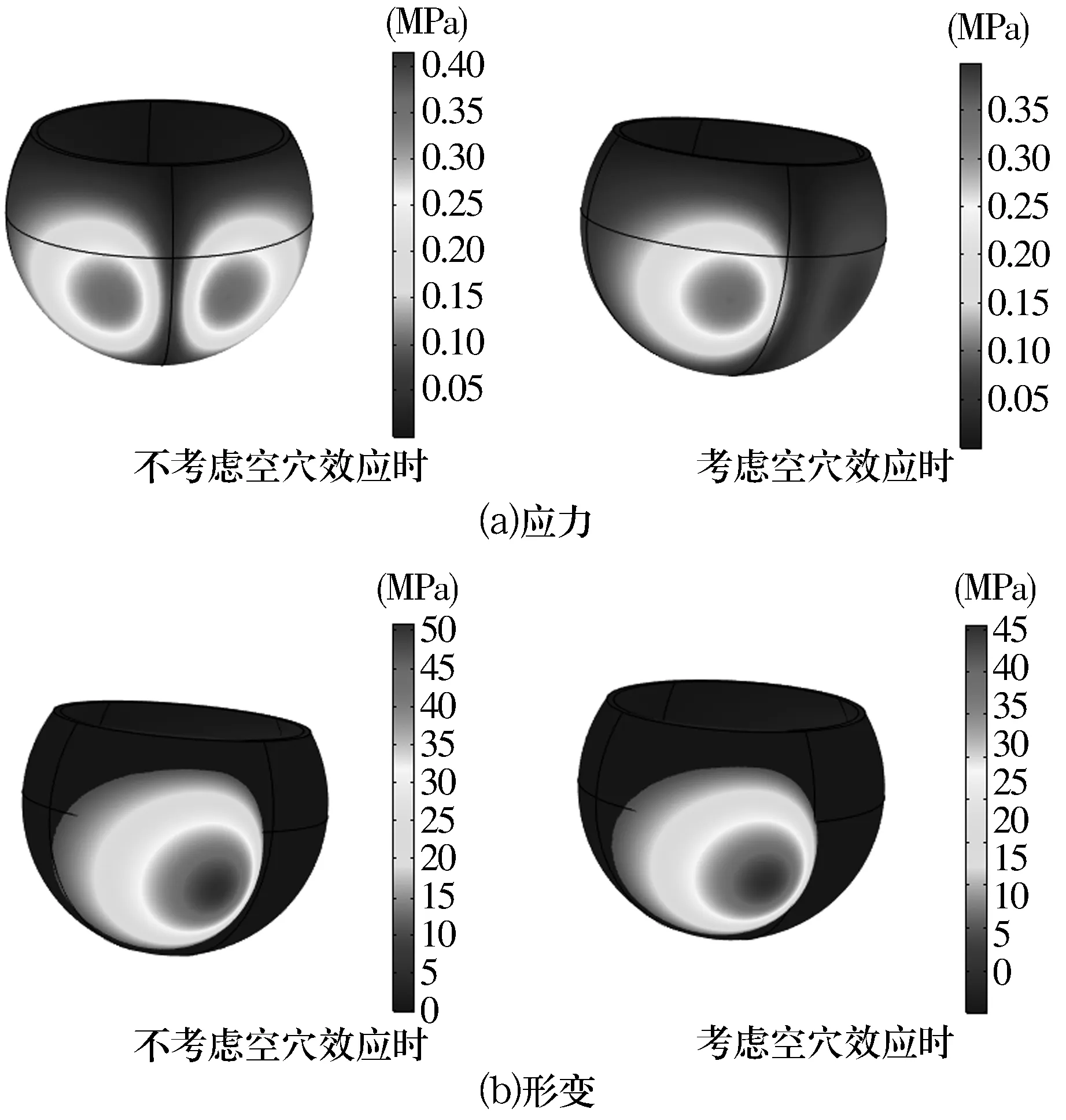
图7 球面轴承应力及形变

有无考虑空穴效应时定子壳赤道处形变如图8所示。由图可知，弧长为0°～100°时2条曲线变化趋势相同；弧长为100°～250°时，不考虑空穴效应时的定子壳形变位移出现第2次高峰，2次高峰分别为收敛区和发散区，考虑空穴效应时的位移曲线在收敛区达到峰值，在发散区出现2个小峰值，直至减小为0。由于定子壳发生弹性变形，与转子壳之间的间隙增大，使得润滑油填充空间更大，从而减小了油膜压力峰值，完成了流固耦合的过程。球面轴承的油膜压力是与外载荷相抗衡的，轴承在几何收敛区产生油膜正压力，同时间隙发散区产生油膜空穴，由于空穴会使轴承过早损坏，所以能够施加到轴承上的载荷值取决于是否形成空穴。

图8 球面轴承赤道处形变位移

5.3 考虑空穴效应下偏心率、转速、定转子间隙及油膜黏度对油膜压力的影响

5.3.1 偏心率

设定转子间隙为78 μm，转子转速为15.7 rad/s时，不同偏心率下球面轴承周向和轴向位置油膜压力分布如图9所示。由图9c和图9d可知，随着周向和轴向偏心率的增大，油膜压力峰值增大，压力分布曲线所包围的面积也相应增大。偏心率过低，油膜压力会过小，从而使得定子壳和转子壳不能分离。

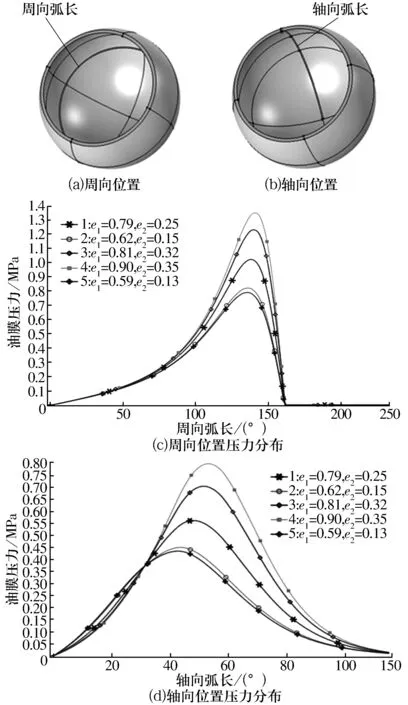
图9 不同偏心率下油膜压力分布图

5.3.2 转速、间隙和黏度

设定转子间隙为78 μm，周向和轴向偏心率分别为0.79和0.25，转速分别为5.6，15.7，21.8，31.4 rad/s时，赤道处油膜压力分布的仿真结果与试验结果如图10所示。由图可知，2种结果吻合度较高，验证了数值仿真结果的准确性。油膜压力峰值随转子转速的增加而增大，且不同转速下油膜压力峰值出现的位置大致相同，证明其与转速大小无关。

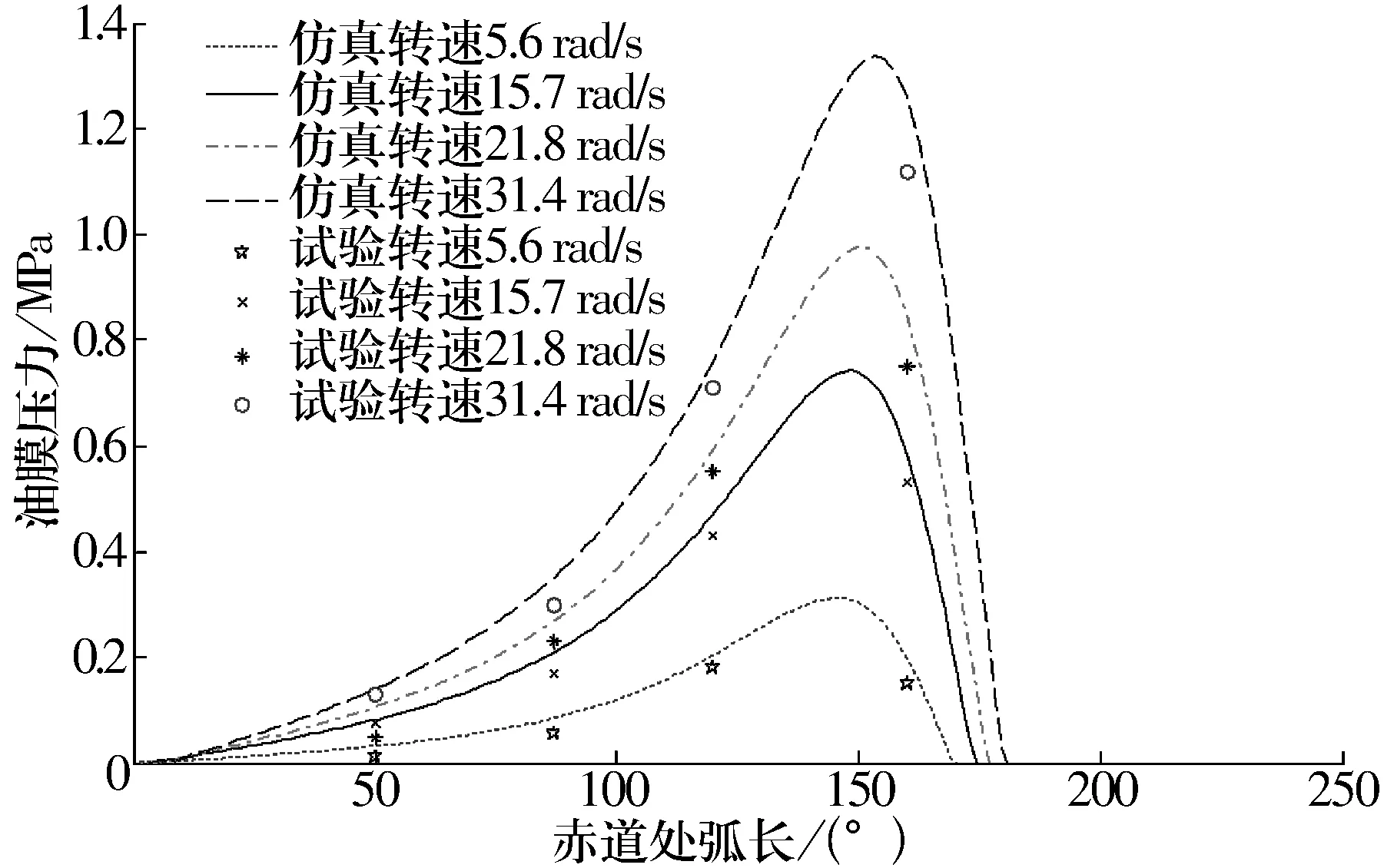
图10 不同转速下赤道处油膜压力分布

转子转速为15.7 rad/s，定子、转子间隙分别为58，68，78，88 μm时，油膜压力分布如图11所示。由图可知，随着定子、转子间隙的减小，油膜压力增大，这是因为间隙减小，油膜厚度减小，而最小油膜厚度决定了油膜压力峰值。

图11 不同间隙下油膜压力分布

定转子间隙为78 μm，周向和轴向偏心率分别为0.79和0.25，转速为15.6 rad/s，油膜黏度分别为0.002，0.008，0.025，0.043，0.062，0.082 Pa·s时油膜最大压力如图12所示。由图可知，油膜最大压力随润滑油黏度的增加呈现明显增大的趋势，表明黏度越高越有利于提高油膜压力及承载力，由于油膜压力不能过大或过小，所以油膜黏度的最优范围为0.008～0.043 Pa·s。

图12 不同黏度下油膜压力分布

5.4 偏心率、转速、定转子间隙及黏度对气相体积分数的影响

不同周向和轴向偏心率下空化区的气相体积分数分布如图13所示。由图可知，随着周向和轴向偏心率的增大，气相体积分数增加。这是由于偏心率的增大加强了定转子间油膜挤压作用，负压峰值增大，从而需要更多的油气化来抵消增大的负压，气化面积增大，故气相体积分数增加。

图13 不同偏心率下油膜的气相体积分数曲线图

不同转速下油膜的气相体积分数分布如图14所示。由图可知，不同转速下球面轴承气相体积分数梯度呈椭圆状分布，分布规律相同，但转速对空化区的面积大小及位置的影响较为显著，空穴区面积随着转速的增加而增大，较大空穴的区域离承载区逐步变远，从而保证了球面轴承承载区油膜的连续性，这是由于油膜自然破裂的位置也在远离承载区。

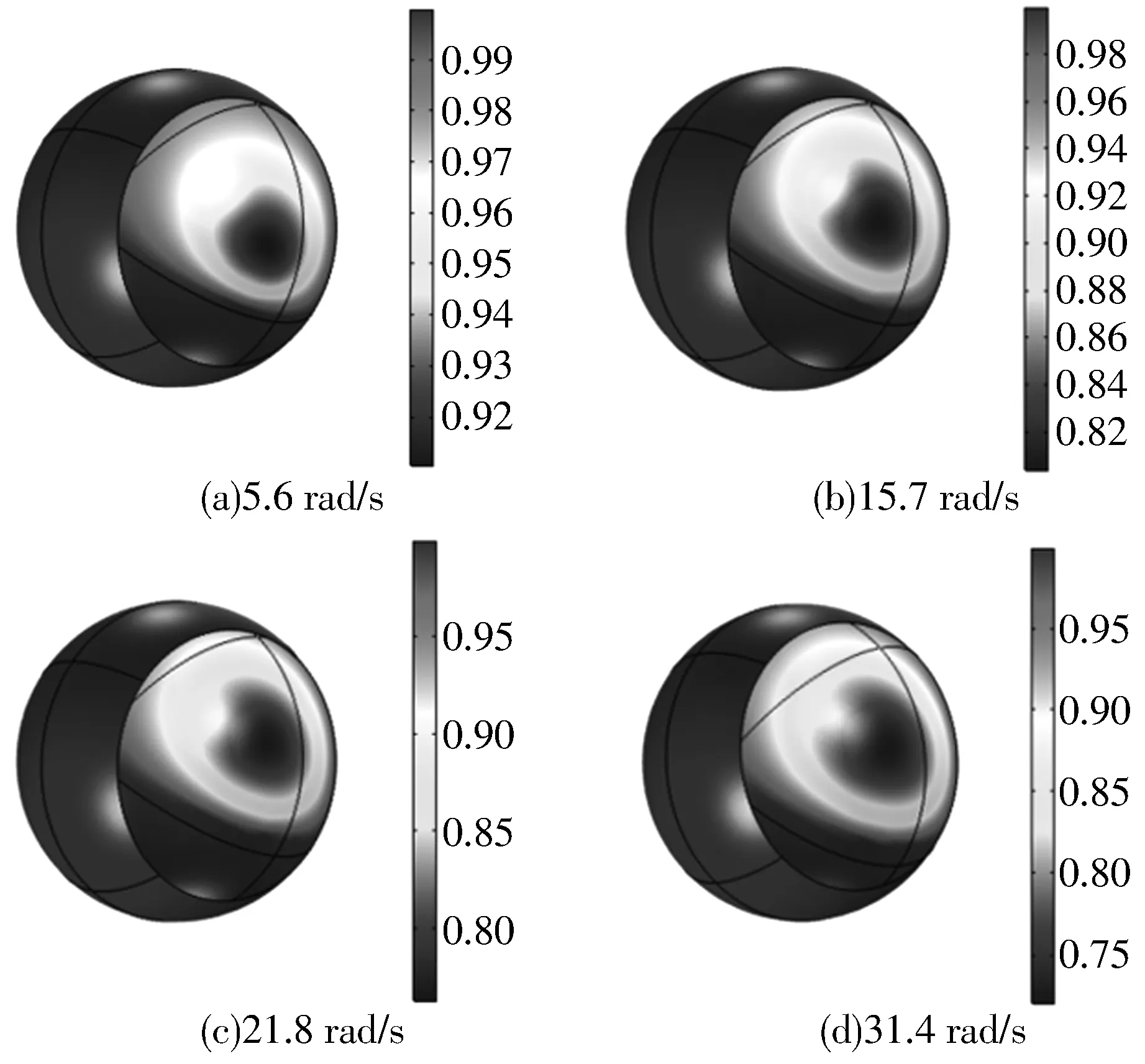
图14 不同转速下油膜的气相体积分数分布图

赤道处不同间隙下油膜的气相体积分数分布情况如图15所示。由图可知，随着定子、转子间隙减小，气相体积分数增大。这是因为间隙减小，油膜压力增大，加剧了空穴现象的发生，因此,气相体积分数比例增大，相应气穴数量增加。

图15 赤道处不同间隙下油膜的气相体积分数分布

不同黏度下油膜的气相体积分数分布如图16所示。由图可知，随着润滑油黏度的增大，空穴区域面积增加，这是由于黏度增大加剧了油膜发散区的空化现象，当润滑油黏度为0.082 Pa·s时，发散区出现了较大面积的空穴区域，气相体积分数为0.5；而黏度为0.008 Pa·s时，空穴面积较小，气相体积分数为0.75。由此可见，黏度的增大会加剧空化现象的发生。因此，选择最优黏度为0.008～0.043 Pa·s的润滑油对电动机的稳定运行具有重要的意义。