基于柔性旋转轮对的车轮多边形磨耗对轮轨力的影响分析

崔 潇，姚建伟，孙丽霞

(1.中国铁道科学研究院 研究生部，北京 100081；2.中国铁道科学研究院集团有限公司 铁道科学技术研究发展中心，北京 100081)

1 刚柔耦合车辆轨道系统及欧拉坐标下的柔性旋转轮对

图1 刚柔耦合车辆轨道系统计算模型

无约束情况下刚柔耦合多体动力学计算公式为

(1)

将式(1)展开可以分为下列2个公式

(2)

(3)

式(3)可推导为如下公式[10]

(4)

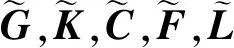
(5)

(6)

(7)

(8)

(9)

(10)

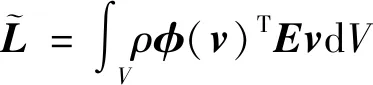
(11)

J=ATAθ,E=-AθθAT

(12)

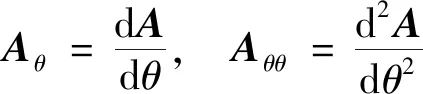
(13)

式中：ρ为柔性车轮密度;Ω为轮对绕车轴轴线转动的角速度；θ为轮对绕车轴轴线转动的角度；φ为欧拉坐标系下的模态；v为欧拉坐标系下的位置矢量；A为旋转矩阵；f(v)为柔性旋转轮对所受的外力矢量；g(t)为柔性旋转轮对所受的外力随时间变化的系数；V为柔性体所占据的体积。

2 车轮多边形旋转效应分析

车轮多边形磨耗属于周期性非圆化磨耗，是车轮不圆顺的一种特殊表现形式。车轮半径沿着整个圆周呈周期性变化。沿一周的波数或边数称作相应的阶数，一般在1～30之间。1～9阶称为低阶多边形，10阶及以上称为高阶多边形。其中，1阶车轮多边形又称为车轮偏心，2阶车轮多边形又称为车轮椭圆化。不同阶数n对应的车轮多边形波长λn为

(14)

式中，R为车轮滚动圆半径。

当列车运行速度为v时，引起的轮轨系统振动频率fn为

fn=v/(3.6λn)=nv/(7.2πR)

(15)

为方便观察车轮多边形磨耗的情况，通常采用极坐标。图2为车轮多边形磨耗示意，以20阶多边形为例，多边形磨耗幅值为0.06 mm，即车轮表面粗糙度为60 μm。

图2 车轮多边形磨耗示意

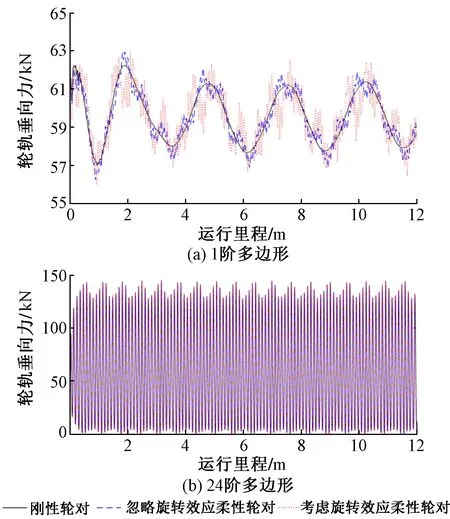
图3 车轮多边形磨耗下轮轨垂向力对比

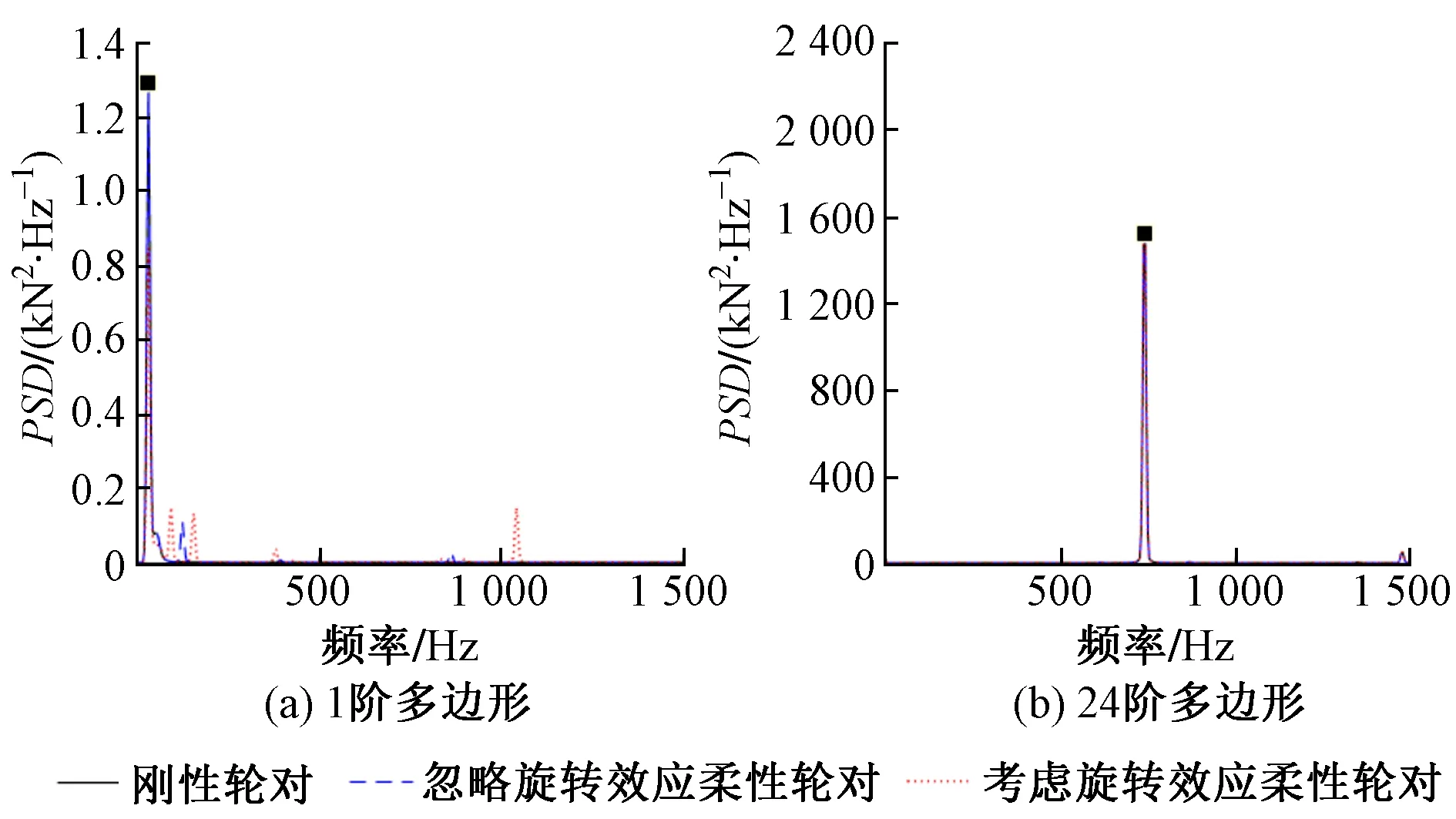
图4 车轮多边形磨耗下轮轨垂向力PSD对比

从图3可以看出，当车轮多边形阶数较低时，考虑旋转效应的柔性轮对其轮轨垂向力的波动，相比刚性轮对和忽略旋转效应的柔性轮对更加剧烈；当车轮多边形阶数较高时，轮轨垂向力幅值较大，最大值约为145 kN，随轨枕位置呈周期性波动。

图4通过对3种轮对建模方法的轮轨垂向力进行频谱分析，可知轮轨垂向力主要存在于与多边形阶数相对应的振动频率(可由式(15)计算得到)，且考虑旋转效应的柔性轮对其轮轨垂向力响应主频存在明显的分离现象。如图4(a)所示，柔性旋转轮对激起了轮轨系统间 1 043 Hz左右的振动主频。图4(b)中轮轨垂向力主频除多边形阶数对应的频率外，还存在1 480 Hz 左右的主频，该频率约为多边形阶数频率的2倍。

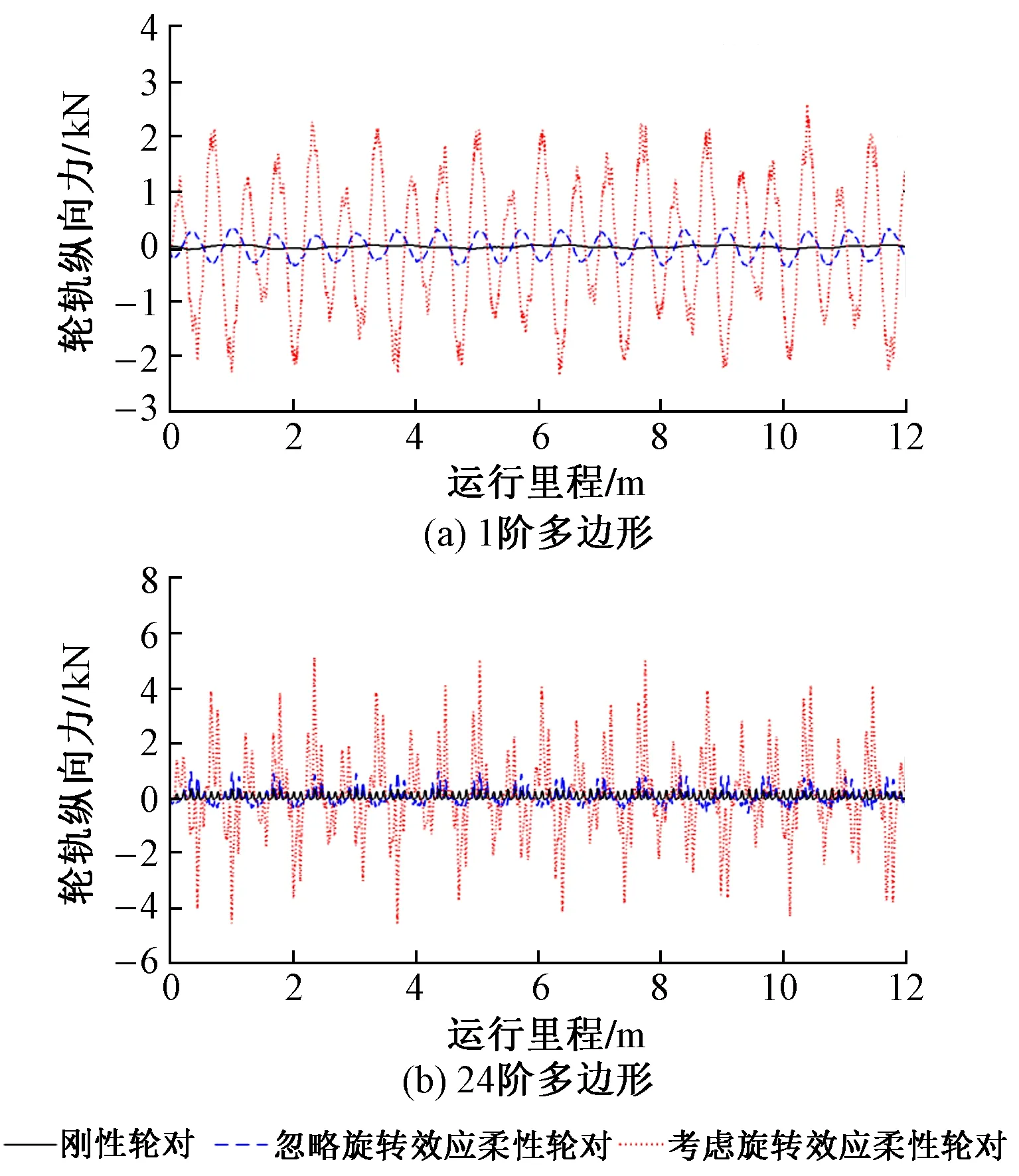
图5 车轮多边形磨耗下轮轨纵向力对比

将刚性轮对、忽略旋转效应柔性轮对以及考虑旋转效应柔性轮对的轮轨纵向力结果进行对比，见图5，并对其进行频谱分析，图6为车轮多边形磨耗下轮轨纵向力PSD对比，频率范围为20～2 000 Hz。

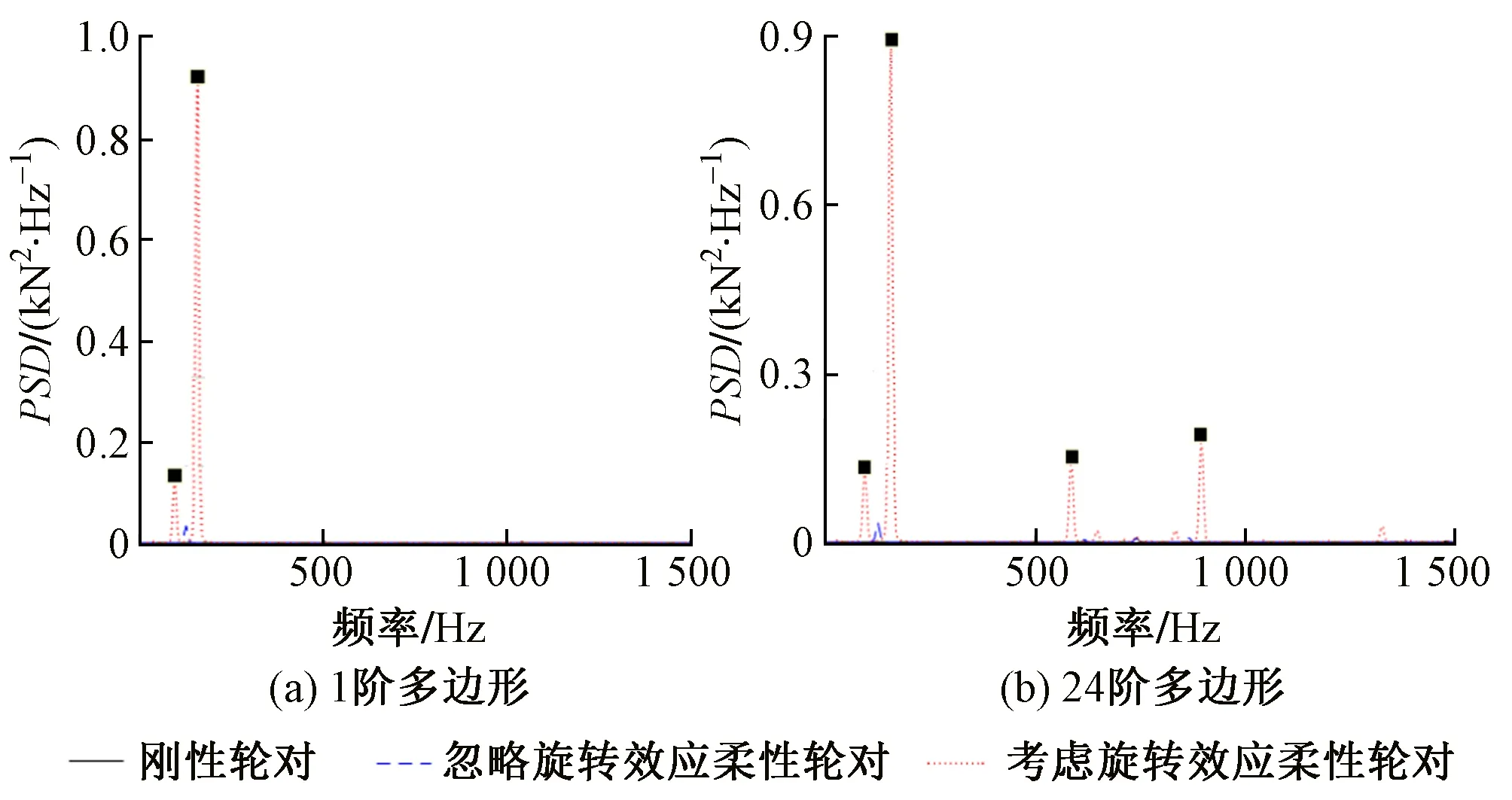
图6 车轮多边形磨耗下轮轨纵向力PSD对比

从图5可以看出，旋转效应对带有车轮多边形磨耗的轮轨纵向力影响较明显，考虑旋转效应的柔性轮对其轮轨纵向力明显大于刚性轮对和忽略旋转效应的柔性轮对。当多边形阶数较低时，阶数对应频率的能量在轮轨纵向力总能量中占比较小，轮对1阶弯曲频率的能量占比较大，柔性旋转轮对对应的分离频率分别约为94 Hz和156 Hz，如图6(a)所示；当多边形阶数较高时，轮轨纵向力存在与多边形阶数频率对应的分离频率，约为586 Hz和895 Hz，分别接近于车轮多边形19阶和29阶的频率，如图6(b)所示。

3 多边形阶数和磨耗程度的影响

3.1 车轮多边形阶数

为了研究车轮多边形阶数对轮轨系统动态响应的影响，将车轮多边形磨耗幅值取定值0.04 mm，阶数取1阶 以及2～30的偶数阶。设列车运行速度为300 km/h。将不同车轮多边形阶数下的轮轨垂向力最大值和最小值进行汇总，见图7。

图7 不同车轮多边形阶数下轮轨垂向力最值

从图7可以看出：随着车轮多边形阶数的增加，轮轨垂向力最大值有总体上升的趋势。当阶数为26阶时轮轨垂向力最大值达到最大，其值约为156 kN；当阶数为24阶、26阶和28阶时轮轨垂向力最小值为0，即车轮发生了瞬时跳动。从轮轨垂向力最值分布来看，轮轨垂向力在车轮多边形为2阶(椭圆化)以及24～28阶时相对附近的阶数波动较大，因此，当车轮存在低阶多边形时，车轮的椭圆化对轮轨系统带来的损坏更严重。为了进一步探究22～32阶轮轨垂向力的波动情况及其原因，选取22阶、26阶和32阶的轮轨垂向力时域和频域结果进行对比分析，见图8。

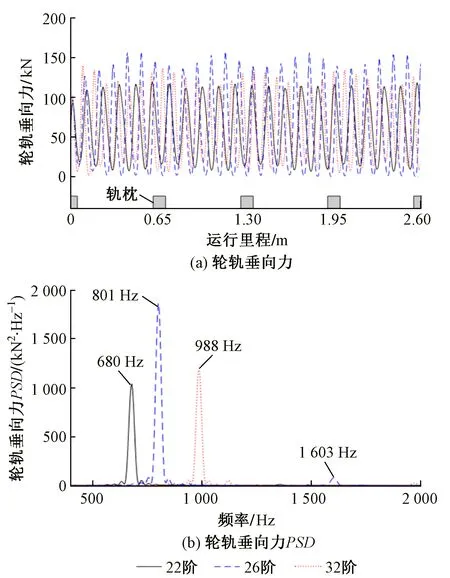
图8 不同车轮多边形阶数下轮轨垂向力结果对比

3.2 多边形磨耗程度

设列车运行速度为300 km/h。为了综合研究车轮多边形阶数和磨耗程度对轮轨系统动态响应的影响，分别将车轮多边形阶数取为1阶以及2～32的偶数阶，并将车轮多边形磨耗幅值取为0.02，0.04，0.06，0.08，0.10 mm。共计85个工况。将不同工况下的轮轨垂向力最大值和最小值进行汇总，见图9。

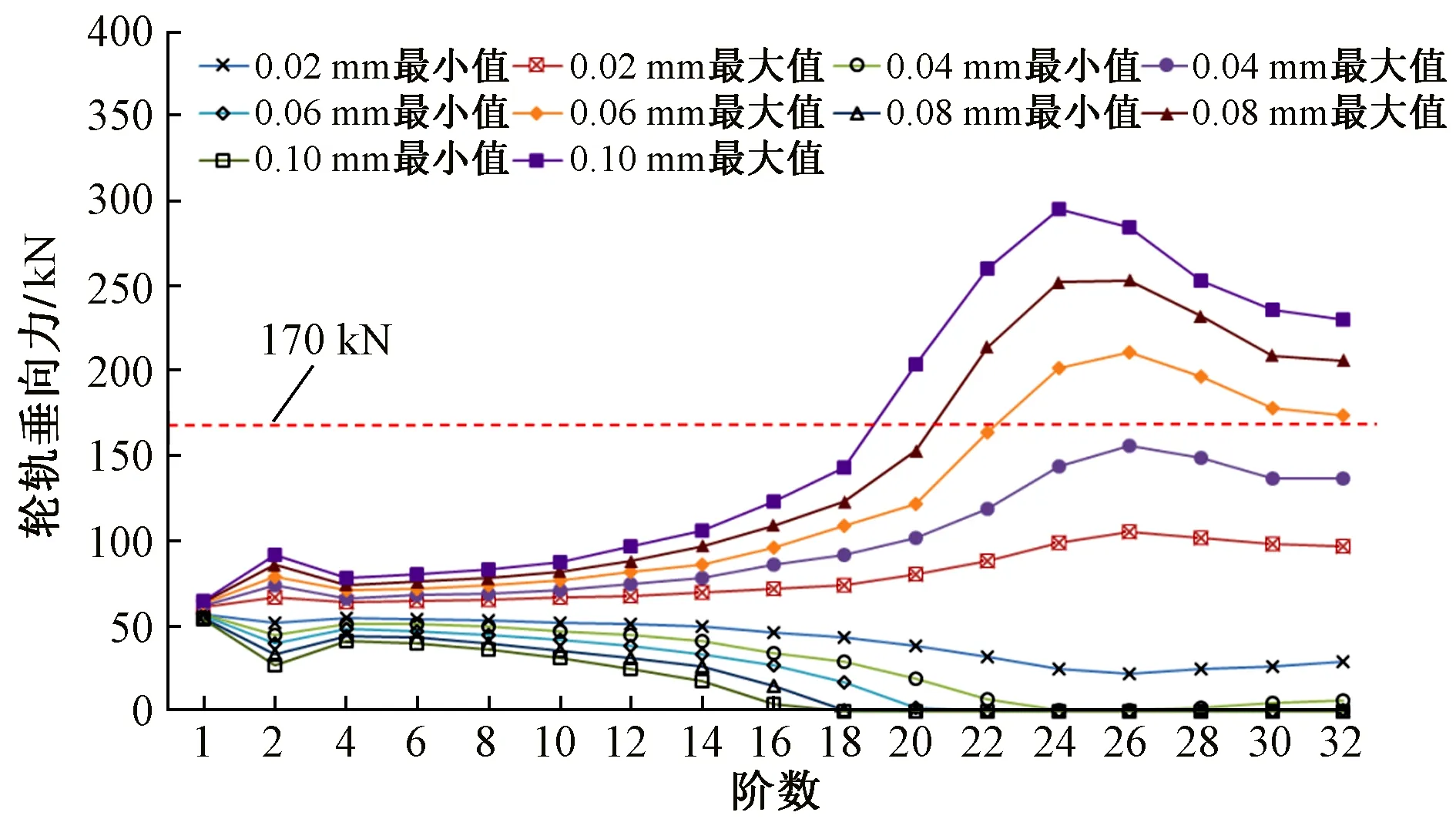
图9 不同磨耗程度和多边形阶数下轮轨垂向力最值

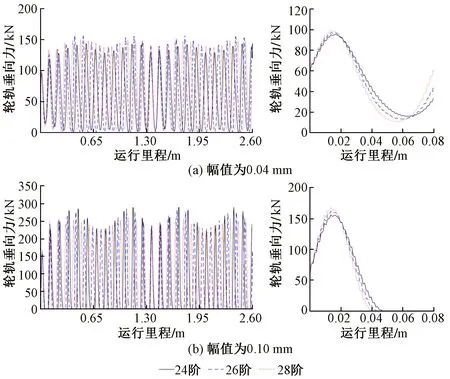
图10 高阶多边形磨耗下轮轨垂向力对比

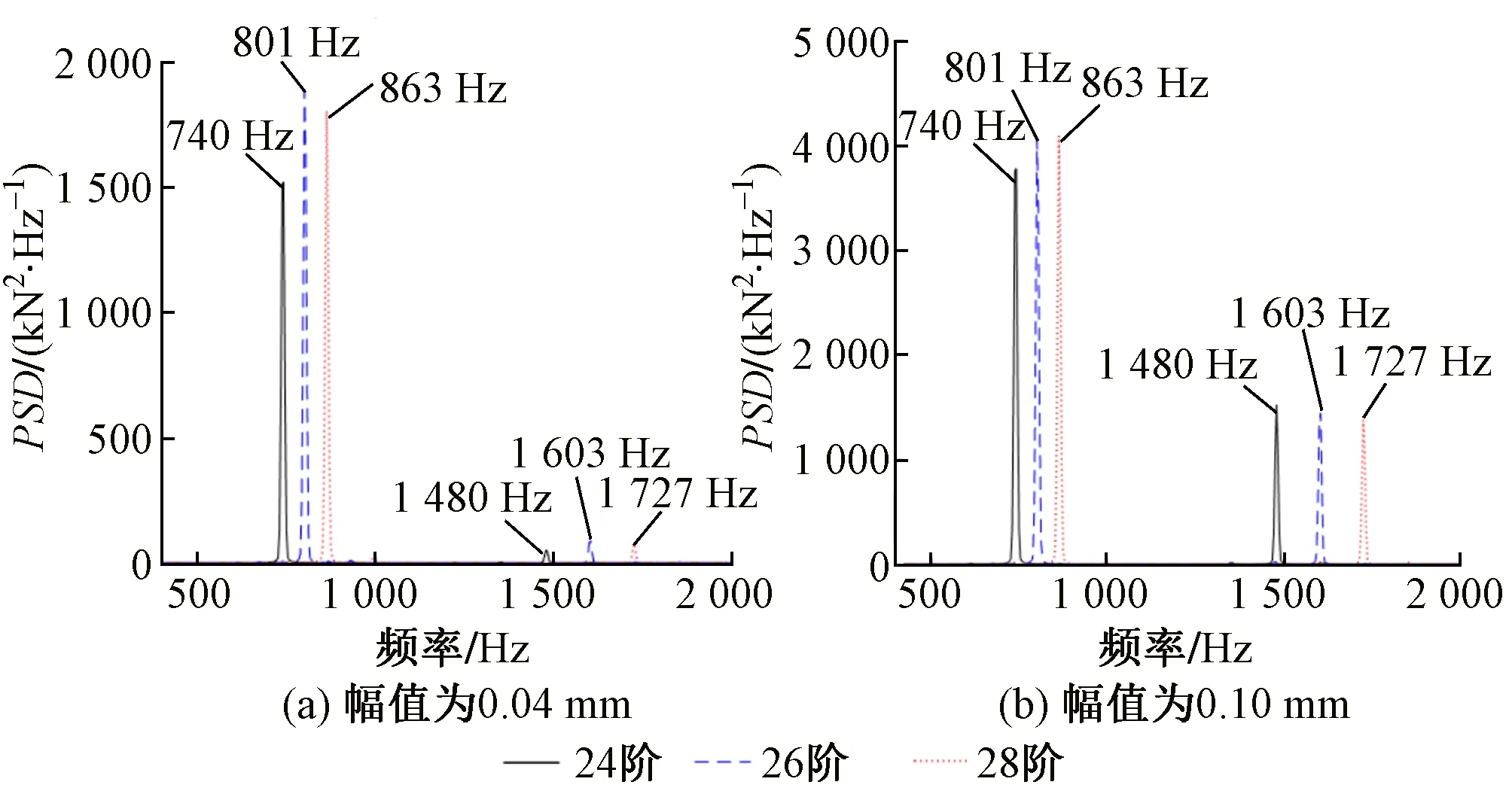
图11 高阶多边形磨耗下轮轨垂向力PSD对比

通过图10可以看出，在列车运行的初始位置(第1个轮轨垂向力波动峰值)，24阶、26阶、28阶车轮多边形磨耗下轮轨垂向力依次递增，但随着列车继续前进，不同阶数多边形磨耗下轮轨垂向力波动幅值发生改变，当多边形磨耗深度为0.04 mm时，26阶多边形磨耗下轮轨垂向力波动幅值大于24阶和28阶时的情况。而当多边形磨耗深度为0.10 mm 时，24阶多边形磨耗下轮轨垂向力波动幅值大于26阶和28阶时的情况。由图11可以看出，这3种阶数多边形磨耗均不同程度地引起了2倍频的振动。当多边形磨耗深度为0.04 mm时，3种阶数多边形对应频率的能量占轮轨垂向力总能量的主要部分，2倍频的能量较小。其中，26阶多边形对应的频率约为801 Hz，2倍频约为 1 603 Hz，这2个主频的PSD均大于24阶和28阶时的情况；而当多边形磨耗深度为0.10 mm时，2倍频能量在轮轨垂向力总能量中的占比明显上升，大于多边形频率PSD的1/3。其中，24阶多边形对应的频率约为740 Hz，2倍频约为 1 480 Hz，24阶频率的PSD小于26阶和28阶时的情况，但其2倍频的PSD大于26阶和28阶时的情况。综上所述，当多边形磨耗严重时，高阶多边形引起的2倍频能量上升，对轮轨力的波动幅值影响较大。

4 结论

1)考虑柔性旋转效应的车轮多边形磨耗下轮轨力响应存在主频分离现象，对轮轨力的波动影响较明显。当多边形阶数较低时，阶数对应频率的能量在轮轨纵向力总能量中占比较小，轮对1阶弯曲分离频率的能量占比较大。

2)当列车运行速度为300 km/h，车轮多边形阶数为24～28阶时，轮轨垂向力出现了拍振现象且波动较大，相对于轨枕位置存在约0.5π的相位超前。当车轮多边形阶数大于22阶且磨耗深度大于0.06 mm时，轮轨垂向力最大值超过限值，需及时对车轮进行镟修或其他养护维修作业。对于多边形阶数大于22阶的高阶多边形，其磨耗深度的限值建议在0.04～0.05 mm。

3)随着车轮多边形磨耗程度的增加，轮轨垂向力最大值由在26阶车轮多边形的情况下出现，逐渐过渡到在24阶车轮多边形的情况下出现，24阶多边形为车轮多边形主要发展趋势。当多边形磨耗严重时，高阶多边形引起的2倍频能量上升，对轮轨力的波动幅值影响较大。