例谈分类讨论思想在等腰三角形问题中的应用

广东省广州市番禺区市桥桥城中学(511400)陈俊霞

清代教育家颜元说过:“讲之功有限,习之功无已.”在数学教学过程中,我们不仅要重视课堂上知识的传授,更要重视“习行之功”.等腰三角形是一种特殊的三角形,其性质丰富多彩,相关问题也灵活多变.一些与等腰三角形的边、角有关的问题,由于条件没有明确给出,会出现多种情况,需要通过分类讨论才能解决.学生遇到等腰三角形中有关分类问题,往往会因为分类不当,或考虑不全面导致错解或漏解,因此要特别引起重视.本文就分类讨论思想在等腰三角形问题中的应用进行举例说明.

一、等腰三角形的分类讨论思想在角中的应用

1、(2018·成都)等腰三角形的一个角为50°,则它的顶角的度数为 ____.

解析题中未指明50°是顶角还是底角,因此应该分两种情况考虑:①当50°是顶角,②50°是底角,顶角度数180°-50°×2=80°.因此答案50°或80°.

点评对于一个等腰三角形,若条件中并没有确定顶角或底角时,应注意分情况讨论,先确定这个已知角是顶角还是底角,再运用三角形内角和定理求解.

二、等腰三角形的分类讨论思想在边中的应用

2、(2017 番禺区期末8)已知等腰三角形的一边长为4,另一边长为8,则它的周长是( ).

A.12 B.16 C.20 D.16 或20

解析已知条件中未指明4,8 是腰长还是底边长,因此需要通过分类讨论来解答.①当4 为腰时,三角形三边分别为4,4,8; ②当8 为腰时,三角形三边分别为4,8,8;由于三角形三边关系必须符合“三角形的两边之和大于第三边”所以排除 ①,三角形的周长为4+8+8=20.答案选择C.

点评对于底和腰不等的等腰三角形,若条件中没有明确哪是底哪是腰时,应在符合三角形三边关系的前提下分类讨论.

三、等腰三角形的分类讨论思想在高中的应用

3、若等腰三角形腰上的高与另一腰的夹角为50°,则这个等腰三角形的底角为____.

解析要注意分高在三角形的内部与高在三角形的外部两种情况讨论,再根据三角形的内角和为180°,等腰三角形的两个底角相等,即可求得结果.

如图1:因为AB=AC,∠ABD=50°,BD⊥AC,所以∠A=40°,所以∠ABC=∠C=(180°-40°)÷2=70°;

如图2:因为AB=AC,∠ABD= 50°,BD⊥AC,所以∠BAC= 50°+ 90°= 140°,所以∠ABC= ∠C=(180°-140°)÷2=20°.

故答案为:70°或20°.

图1

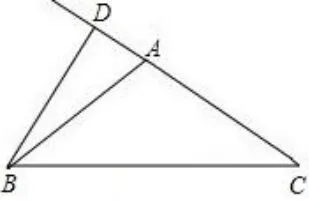
图2

点评三角形的高是由三角形的形状决定的,对于等腰三角形,当顶角是锐角时,腰上的高在三角形内;当顶角是钝角时,腰上的高在三角形外.

四、等腰三角形的分类讨论思想在垂直平分线中应用

4、已知等腰△ABC中,AB=AC,若AB的垂直平分线与边AC所在直线相交所得锐角为40°,则等腰△ABC的底角∠B的大小为多少?

多位熟悉林雪川情况的知情人向上游新闻记者介绍，林雪川初中毕业后在观阁镇当地的邮电部门送报纸，开始时工作较为认真。但不久之后，林雪川利用送报纸的机会，以帮村民取邮政汇款为由，多次偷窃村民从省外汇回家乡的款项。被村民发现之后，林雪川前往广东打工，因数额不大，警方也未予追究。

解析由条件“AB的垂直平分线与边AC所在直线相交”可知,其交点可能在腰AC上,也可能在AC的延长线或反向延长线上,因此,应当分两种情况讨论.

①DE与线段AC相交时,如图3,因为DE是AB的垂直平分线,∠AED= 40°,所以∠A= 90° -∠AED=90°-40°=50°,因为AB=AC,所以∠ABC=0.5(180°-∠A)=0.5(180°-50°)=65°;

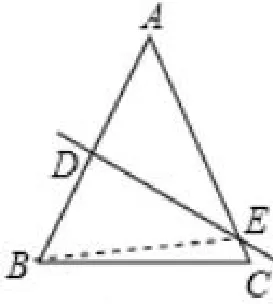
图3

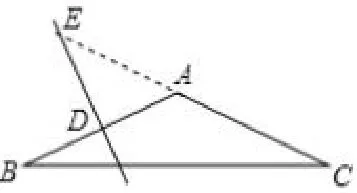
图4

②DE与CA的延长线相交时,如图4,因为DE是AB的垂直平分线,∠AED= 40°,所以∠EAD=90°-∠AED=90°-40°= 50°,所以∠BAC= 180° -∠EAD= 180° -50°=130°,因为AB=AC,所以∠ABC=0.5(180°-∠BAC)=0.5(180°-130°)=25°.

点评由于受定式思维的影响,学生大部分遗漏第二种情况.建议解题时按照三角形的分类(按角),画出所以情况在进行讨论,可以做到不缺不漏.

五、等腰三角形的分类讨论思想在中线中应用

5、已知一个等腰三角形底边的长为5cm,一腰上的中线把其周长分成的两部分的差为3cm,则腰长为____.

解析中线把等腰三角形分成两部分,已知条件没有指明哪部分长,故有两种可能.如图,因为BD是△ABC的中线,所以AD=CD,所以两三角形的周长的差等于腰长与底边的差,因为BC=5cm,所以AB-5=3 或5-AB=3,解得AB= 8 或AB= 2,若AB= 8,则三角形的三边分别为8cm、8cm、5cm,能组成三角形,若AB=2,则三角形的三边分别为2cm、2cm、5cm,因为2+2=4＜5,所以不能组成三角形,综上所述,三角形的腰长为8cm

点评 涉及等腰三角形边的计算时,要明确它是否能构成三角形.

六、等腰三角形的分类讨论思想在动态题目中应用

解析(1)若AO作为腰时,有两种情况,OA=OP,AO=AP与x轴的交点,有3 个; (2)若OA是底边时,P是OA的中垂线与x轴的交点,有1 个.以上4 个交点没有重合的.故符合条件的点有4 个.

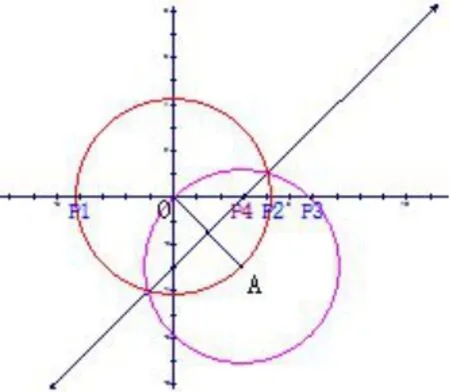
图5

点评 在作以某一线段为边的等腰三角形时,如果没有明确这是底还是腰,则需进行分类,并确定顶角到底是哪个,做到不缺不漏.

7、在网格中,网格线的交点称为格点.已知A、B是两个格点,如果点C也是图6中的格点,且使得△ABC为等腰三角形,则点C的个数是( )

A.6 B.7 C.8 D.9

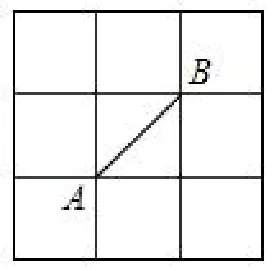
图6

图7

解析在网格背景下建议捉住分类标准利用圆规数形结合解决问题.如图7:分情况讨论.①AB为等腰△ABC底边时,符合条件的C点有4 个; ②AB为等腰△ABC其中的一条腰时,符合条件的C点有4 个故选:C.

点评最容易漏掉,求解时一定要认真分析题意,画出所有可能的图形,这样才能正确解题.

8、已知△ABC中,AB= 3,AC= 5,BC= 7.在△ABC所在平面内一条直线,将△ABC分割成两个三角形,使其中有一个边长为3 的等腰三角形,则这样的直线最多可画( )

A.2 条 B.3 条 C.4 条 D.5 条

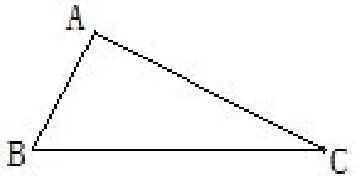
图8

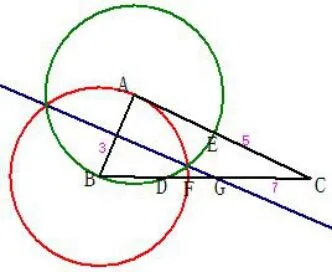
图9

解析边长为3 的等腰三角形未能明确那条边为3,故可能是腰长为3,底边为3.如图9,①以AB为腰,有两种情况(1)以A为圆心,AB为半径画弧,交于点D、E,(2)以B为圆心,AB为半径画弧,交于点F; ②以AB为底边,则AB的垂直平分线交BC于点G.故答案有4 条,选择C.

点评在作以某一线段为边的等腰三角形时,如果没有明确这是底还是腰,则需进行分类,并确定顶角到底是哪个,借助圆规作图,做到不缺不漏.

9、如图10,在△ABC中,∠B= 60°,AB= 12cm,BC= 4cm,现有一动点P从点A出发,以2cm/秒的速度沿射线AB运动,则运动几秒时△PBC为等腰三角形?

图10

解析点在射线上运动,故有两种可能,P在线段AB上,P在线段AB外.设运动t秒时△PBC为等腰三角形,则AP=2t,BP=AB-AP=12-2t.①当点P在线段AB上时,如图11,因为∠B= 60°,△PBC为等腰三角形,所以△PBC是等边三角形,PB=BC=4cm,所以12-2t=4,所以t= 4 秒; ②当点P在线段AB外时,如图12,因为∠P′BC= 120°,所以BP= 2t-12,因为PB=BC,所以2t-12=4,所以t=8 秒.故运动4 秒或8 秒时△PBC为等腰三角形.

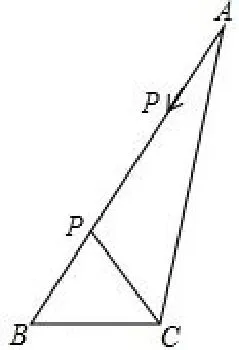
图11

图12

点评在等腰三角形动点问题中,要明确运动范围是什么,将所有情况罗列出来在进行讨论.

在等腰三角形问题中,很多问题需要涉及分类思想.学生要依据题目给出的关键词思考为什么要进行分类,如何进行分类,怎样确定分类.要做到真正掌握学习方法、学习思想,达到懂一题、晓一类、通一片.愿所有的学生在学习和生活中都能够像分类讨论一样多方面考虑问题、认识问题、并解决问题!