谈数学中的构造法

陕西省咸阳市乾县大墙九年制学校(713302)范亚飞

数学是一门创造性的艺术,蕴含着丰富的美,而灵活、巧妙的构造令人拍手叫绝,能为数学问题的解决增添色彩,更具研究和欣赏价值.所谓构造法是指当某些数学问题使用通常办法按定势思维去解决很难奏效时,应根据题设条件和结论的特征、性质、从新的角度、用新的观点观察、分析、解决对象,抓住反映问题的条件与结论之间的内在联系,把握问题的外形、数值等特征,用已知条件中的元素为“元件”,用已知数学关系式为“支架”,在思维中构造出满足条件或结论的数学对象,使原问题中隐晦不清的关系和性质在新构造的数学对象中清楚的展现出来,从而借助该数学对象简捷的解决数学问题的方法.

构造法作为一种数学方法,本质特征是“构造”,其主要特点也是“构造”.在运用时,一要明确构造的目的,即为什么目的而构造;二要弄清问题的特点,以便依据特点,确定方案、实现构造,下面举例说明这些.

一、构造方程

方程式是解决数学问题的一个重要工具,许多数学问题,根据其数量关系,在已知和未知之间搭上桥梁,构造出方程,使解答简捷、合理.运用方程观点解题可归结为3 个步骤:(1)将所面临的问题转化为方程问题;(2)解这个方程或讨论这个方程的有关性质(常用判别式与韦达定理)得出相应的结论;(3)将方程的相应结论再返回为原问题的结论.

例1已知a,b,c为互不相等的实数,试证:

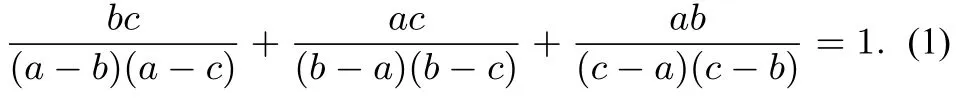
证明构造方程

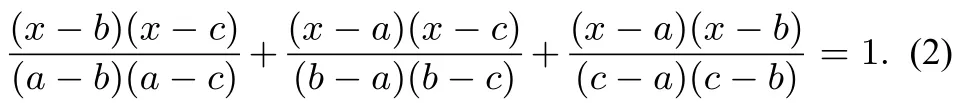
显然a,b,c为方程的三个互不相等的实根.面对任意实数x均满足(2)式.特别地,令x=0,即得(1)式.

例2若p,q ∈R,p3+q3=2.求证:0＜p+q≤2.

证明由p3+q3=2,有(p+q)3-3pq(p+q)=2.显然p+0,令p+q=k,则构造方程

则p,q显然是方程(1)的二实根,于是0,即解得0＜k≤2,即0＜p+q≤2.

例 3设x,y为实数,且满足关系式:则x+y=____.

分析此题用常规方法,分别求出x和y的值后再求x+y既繁又难,三次方程毕竟不熟悉.若将两方程联立构造出方程(x-1)3+1997(x-1)=(1-y)3+1997(1-y)=1,利用函数f(t)=t3+1997t的单调性,易得x-1 = 1-y,即x+y=2,自然、简洁.

二、构造函数

在求解某些数学问题时,根据问题的条件,变换思维的角度,构想、组合一种新的函数关系,题在新的函数观点下实行转化,并利用函数的有关性质解决原问题是一种行之有效的解题手段,是实现数学中从常量到变量的这个认识的飞跃.很多数学命题转化为研究函数的性质,并利用函数的单调性、有界性、奇偶性等使繁冗复杂、难寻入口的问题得到巧妙和别具一格的解决.

例1(柯西不等式)设ai,bi(i= 1,2,··· ,n)均为实数,证明:

证明; 构造二次函数即,f(x)= (a1x+b1)2+(a2x+b2)2+···(anx+bn)2≥ 0,所 以 Δ =不等式得证.

例2设f(x)在[a,b]上连续,在(a,b)内可导,且ab ＞0,求证:∃ξ ∈(a,b)使2ξ(f(b)-f(a))=(b2-a2)f′(ξ).

证明只需构造g(x)=x2,则可知g(x)在[a,b]连续,在(a,b)内可导; 且在(a,b)内g′(x)≠0,故应用柯西定理有即2ξ(f(b)-f(a))=(b2-a2f′(ξ).

例3已知求α+β.

分析与解注意到两个已知等式的左边具有相同的结构,故可构造辅助函数f(x)=x3-3x2+5x,进而化成f(x)=(x-1)3+2(x-1)+3,再引入函数g(u)=u3+2u,则f(x),g(x)之间有关系g(x-1)=f(x)-3.易见g(u)是单调上升的奇函数，而题中的条件变成g（α- 1）= f（α）-3= -2，g（β- 1）= f（β）- 3 = 2 由g（u）的性质知α- 1，β- 1在x 轴上关于原点对称故有（α- 1）+（β- 1）= 0，因此得α + β = 2.

例4设函数f（x）在［0，1］上连续，f（0）= 0，在（0，1）内0 ＜ f '（x）＜ 1.证明：

证明构造函数所以φ（x）为单调增函数.x = 0 时，φ（0）= 0.故φ（x）≥ 0，即F'（x）≥ 0.所以F（x）为单调增函数，F（0）= 0，故F（1）≥ F（0）= 0，既成立.

三、构造数列

涉及与自然有关的不等式的证明时，可以用数学归纳法，但若用构造递增数列（或递减）数列的方法，有时会更简便一些.

例1设都大于- 1且同号，求证：

证明构造数列则

证明不等式的方法有很多，构造法就是其中的一种，其实质是将不等式进行等价转化.它以构造数列、图形、方程作为常用手段.以下就以构造数列、图形为例来谈.

由以上两例可以得出构造图形的要点是：仔细审题，绘出符合题设、能部分或全部体现题意并反映各数量关系的几何图形，借助几何图形来解决问题.

从以上各例不难看出，构造法是一种极富技巧性和创造性的解决问题的方法，体现了数学中发现、类比、化归的思想，也渗透着猜想、探索、特殊化等重要得数学方法，而在构造时，要以观察为先导、以分析为武器、以一定的知识背景、通过仔细观察、分析、去发现问题的各个环节以及其中的联系，从而为寻求解法创造条件.另外，运用构造法解数学题可以从中欣赏数学之美，感受解题的乐趣，更重要的是可开拓思维空间、启迪智慧、并对培养多元化思维和创造精神大有裨益.

［1］李明振.《数学方法与解题研究》.上海科技教育出版社，2003（9）.

［2］华东师范大学数学系编《数学分析》.高等教育出版社，2002（1）