项目反应理论在几类数学试题编制与评价中的应用

广东省北京师范大学(珠海)附属高级中学(519080)黄嘉鹏

一、项目反应理论简介

在任何一场大型考试中,对试题质量的科学分析评价,是对考试结果有效性的重要检验,更是指导后续教学的重要参照物.目前较为盛行的评价理论,主要有经典测量理论和项目反应理论.

经典测验理论(Classical Test Theory)的理论架构简单,采用的计算公式浅显,在历史上为心理测量学的发展做出过巨大贡献,也是目前测验学界使用较为广泛的理论依据.但它却有着许多先天的不足之处:(1)观察分数等权重累计的不合理性:(2)对被试的评价与对试题的评价相互依赖; (3)被试能力与试题难度的非统一性;(4)测量误差估计的不精确性和笼统性.[1,2]

项目反应理论(Item Response Theory)正是为了改进经典测量理论的这些先天不足而出现的.相比经典测量理论,它具有如下的优点:(1)试题参数和被试能力参数的不变性;(2)被试能力和试题难度的统一性;(3)对试题测量误差估计的精确性.由于项目反应理论具有上述优点,我们可以通过它获得较准确的被试能力参数和试题参数,判断试题是否合理,完成鉴别学生的能力差异等评价工作.[1,2]

二、基于项目反应理论的试题质量分析[2]

1.试题特征曲线(Item Characteristic Curve)

基于项目反应理论,我们认为在一次考试中,学生的潜在能力与学生的作答结果之间存在一种关系,这种关系可以用一条单调递增的S 型连续函数来近似模拟.我们把被试能力值作为自变量,把被试答对试题的概率作为因变量,那么由不同能力的考生答对题目概率的关系散点拟合得到的曲线,就称为试题特征曲线.

在单参数和双参数Logistic 模型中,试题特征曲线的拐点(同时也是曲线的中心),就是纵坐标为0.5 的点.

2.难度参数b

项目反应理论认为,试题的难度是试题本身所具有的一种特性,与被试样本无关.难度参数b的取值就是试题特征曲线拐点处的自变量的值.换句话说,在单参数和双参数Logistic 模型中,能力值等于试题难度的考生答对该题的概率为0.5,能力值高于试题难度的考生答对的概率高于0.5,反之则低于0.5.

难度参数b 值越大表示试题越困难,b 值越小表示试题越简单.

3.区分度参数a

异于经典测量理论,项目反应理论中的区分度参数a 表示的是试题特征曲线拐点处切线的斜率.区分度参数a值越大,表示该试题对于能力在试题难度附近的考生的区分作用越大,反之则作用越小.

我们需要特别注意的是,项目反应理论中的区分度,主要是相对于能力落在拐点附近的考生而言,而不是针对整个的被试群体而言.

4.伪机遇参数c

试题特征曲线的下渐近线y=c中的常数c称为伪机遇参数,它反映的是能力低下的考生答对该试题的概率.值得一提的是,伪机遇参数并不是考生随机作答的正答概率.伪机遇参数对所有被试的正答率会有所影响,但它对能力水平高的考生影响非常小,而对能力水平低的考生影响却非常大.

上文中提及的单参数Logistic 模型,指的是仅包含难度参数b的模型.而双参数和三参数模型,分别指的是包含参数a、b的模型和包含参数a、b、c的模型.

5.试题信息函数(Item Information Function)

项目反应理论提出了一个用于描述试题与诊断试题的依据,那就是试题信息函数.某个试题的信息函数能展现出该试题对被试能力估计的有效性有多大,从而判断试题对于整个考试的贡献有多大.

整份试卷所有试题的信息函数累加得到的结果,称为总信息函数.

三、项目反应理论在几类数学试题编制与评价中的运用方法

1.课堂小测

课堂小测主要用于对学生某项知识或能力的检查或训练,随堂检验学生理解掌握的情况和学习状态.这种考试无需具备选拔和区分的能力,所以对区分度参数的要求极低.而从加强学生双基和增强学生学习兴趣方面入手的话,应选择难度系数适中或偏低的题目组成试题.此类小型考试的试题评价,主要依赖于难度参数和试题内容,对其他参数信息的要求较低.

2.阶段性考试

这是多见于学生完成了某一阶段的完整学习,并在教师的指导下进行了系统复习之后的一种考试,如单元考试、期中期末考试.这种考试主要目的在于检验学生学习成果和教师教学效果,并根据考试结果进行学习和教学策略的调整.此类试卷的试题编制过程中,我们需要挑选各种不同难度的题目以适应能力水平不同的全体学生,并注意试题的典型性和区分度.其试题评价主要依赖于试题特征曲线、难度参数、区分度参数和试题信息函数.

3.通过性考试

此类考试的目的是为了检验考生是否达到了某个预先设定的标准.这种标准包括了内容标准(学生是否掌握了所需的知识或能力)和分数标准(通过分数来说明学生掌握所需的知识或能力的比例,进而评价是否达标).内容标准关心的是题目本身是否覆盖了所要考查的知识或能力;分数标准则是要求试题具有足够的代表性,然后用一个划界分数作为标准来体现学生的学习能力和掌握情况.

为了让考试结果更好地反映考生的水平,提高划界分数对考生水平的正确判断率,我们需要尽量降低测量误差.罗照盛老师在《项目反应理论基础》一书中指出,这类试题的命制要使得各部分内容之间的试题参数指标分布接近,同一部分内容之间的难度分布均匀,区分度指标不低于0.3,考试的总信息函数的图像是单峰的,并在划界分数附近取得峰值.[1]按照这个标准,我们编制试题时,需要在各部分考查内容中,精心挑选具有适合的难度和高区分度的题目,同时还要求其试题信息函数在划界分数附近取得最大值.而此类考试的试题评价,也主要依赖于难度参数、区分度参数、试题信息函数和总信息函数.

4.选拔性考试

选拔性考试的主要目的在于选拔,也就是要把能力水平不同的考生准确地区分出来,找出他们在群体中的相对排位.根据选拔性考试的目的,试卷应该能够使得能力水平不同的学生的得分是不一样的.那么,这些试题应该具有较好的代表性,且在全部能力范围内具有较高区分能力.为了实现这种效果,考试的总信息函数图像必须是呈高原状的.[1]

按照这个思路,我们编制此类试题时,需要先设定总信息函数,然后精心选取多种不同难度且区分度较高的题目,并使得各个试题信息函数的和可以尽量填满设定的总信息函数以下的位置,且没有突兀的高点,最后对试题再进行优化组合.这类考试的试题评价,对试题各种信息参数的要求都比较高,尤其是区分度参数和试题信息函数.

5.学科竞赛

学科竞赛类的考试是为了优中选优,筛选出知识掌握程度最佳、能力水平最高的一批考生.这种考试的试题难度较大,且应该不能被学生轻易猜中答案.所以,较佳的难度参数和尽可能低的伪机遇参数是我们挑选试题的重要参照指标,当然也是我们评价试题的重要指标.

四、项目反应理论在试题分析中的具体应用

在本节中,我们将以珠海市期末全市统考的理科数学A卷试题为例,基于项目反应理论,运用软件PARSCALE4.1,使用Logistic 三参数模型,对试题进行分析评价.

本次考试共有3591 位学生参加,由于数据量不是特别大,所以我们不进行抽样,而是直接对试题和全体考生的作答结果进行分析.

1、试题宏观分析

本次统考试卷中,客观题(单选题和填空题)共18 道,占90 分;主观题(解答题)共5 道,占60 分.

本次考试作为期末统考,属于阶段性考试,目的是为了对教学质量进行检验,试题的理想状态应该是在能力全距上均有较高信息量.

从图1中可以看到,试题的总信息函数呈双峰状,在能力水平区间[-2,2] 之间均有较大信息量; 整套试题的总信息量在能力水平中等偏下的-1.1 处和能力水平中等偏上的1.3 处分别取得9.76 和11.38 的两个信息量峰值,这两处标准误最小,分别为0.103 和0.074;信息量最少的地方出现在能力水平为3 的地方,此处信息量仅有0.71,标准误最大,达到1.18.

整体而言,整份试题用于鉴别不同能力水平的学生是比较有效的,尤其对鉴别中等能力水平附近的学生所起的作用更加明显.唯一美中不足的就是比较欠缺高质量的难题,这可能会使得最优秀的那部分学生得不到区分.

图1 试题信息量、标准误和考生能力参数之间的关系

2、试题微观分析

下边我们将分别使用二元计分和部分计分模型对客观题和主观题进行微观分析.

①客观题部分

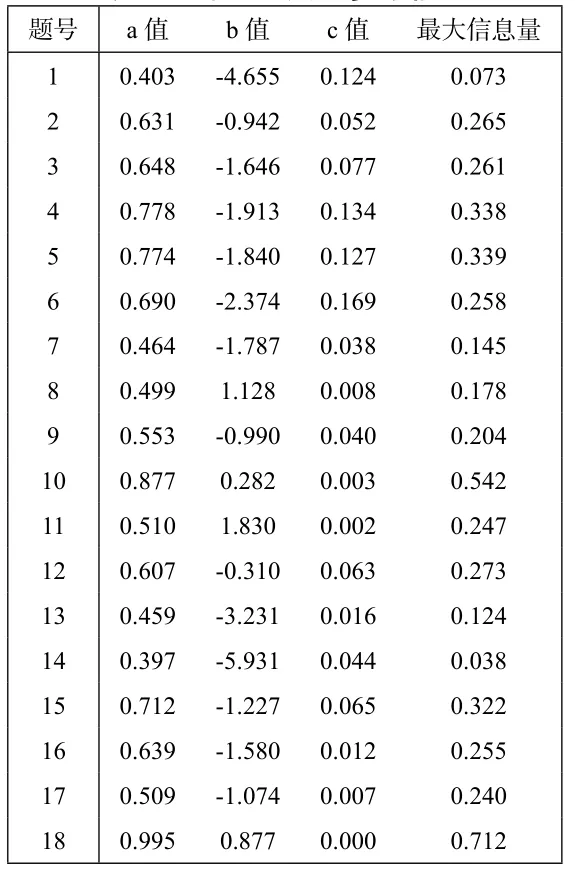
表1 客观题试题参数信息

18 道客观题的参数信息如表1所示.试题难度跨度较大,但高质量的难题较少;大部分题目的区分度较高,提供的信息量较丰富;但也有少量题目不尽如意.

其中,最优质的题目有第18、10、5、4、15 题.以第18 题为例(图2),该题的信息函数提供信息量最大,试题特征曲线形态良好;区分度达到了0.995,可以很好地区分不同能力水平的学生;难度为0.877,适合中等偏上水平的学生.如果考虑建立题库,那么这种题目就是较佳的选择.

较差的题目有第14、1 题.以第14 题(图3)为例,该题的试题特征曲线整体偏高且平缓,区分度较小,难度很低;试题信息函数几乎与x轴平行,提供的信息量非常低.这种题目不适宜加入通过性考试、选拔性考试和学科竞赛类的试题库,应作为课堂小测或是阶段性考试的送分题.

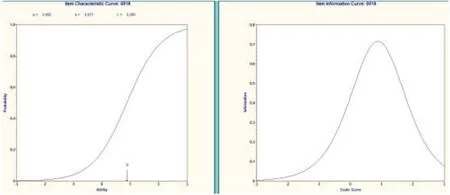
图2 第18 题的试题特征曲线和试题信息函数

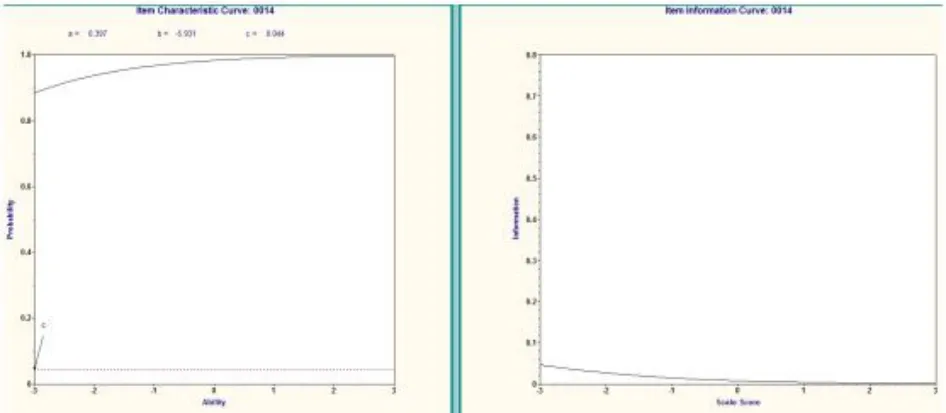
图3 第14 题的试题特征曲线和试题信息函数

②主观题部分

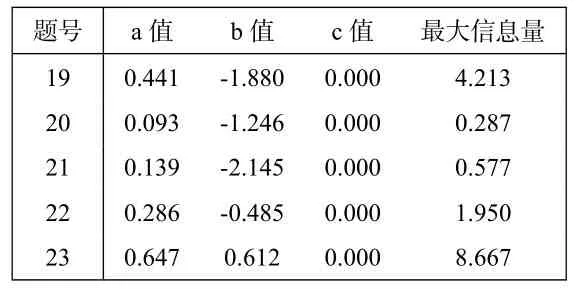
表2 主观题参数信息

5 道主观题的参数信息如表2所示.主观题难度相比客观题较大,整体提供信息量远大于客观题.

其中第19、22、23 非常优质.以第23 题(图4)为例,不同能力水平的学生对应不同分值的特征曲线差异非常明显;信息函数在较大范围内均能提供较多的信息量,尤其对鉴别中等偏上水平的学生作用非常明显.我们建议在建立题库的过程中保留此题目.

第20 题(图5)较不理想.试题不同分值的特征曲线均比较平缓,也就是说不同能力的学生获得各种分数的可能性比较随机;试题整体提供的信息量也不足.建立题库的过程中,建议删除此题.

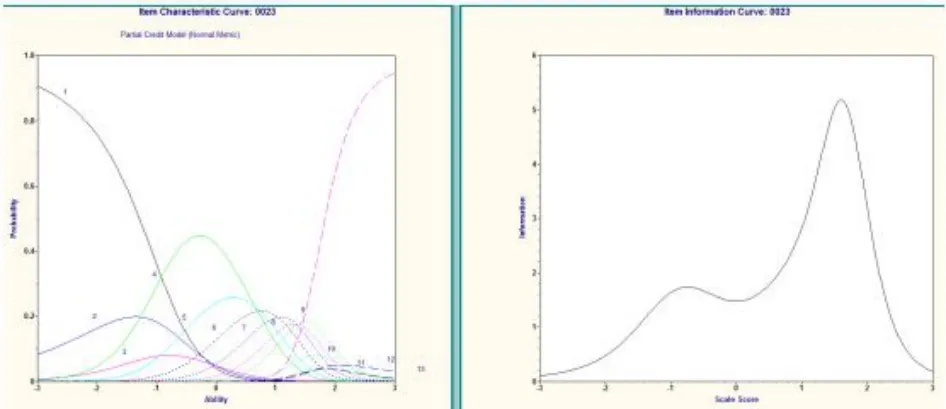
图4 第23 题的试题特征曲线和试题信息函数

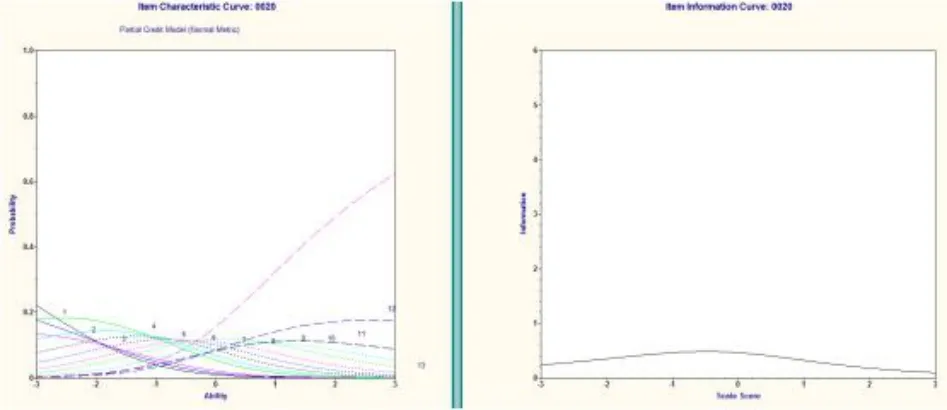
图5 第20 题的试题特征曲线和试题信息函数

五、项目反应理论的应用前景

当今社会,升学、招聘、行业准入等都需要考试.社会对考试的需求正日益增长,对考试质量的要求也在不断提高.在这样的时代浪潮下,项目反应理论展现出了勃勃生机:

1.题库建设

大规模的高质量的题库是高质量考试所必备的.可以想象,在具备合适的人力、管理和时间成本的情况下,我们可以运用项目反应理论,通过大量考试试题的参数信息进行分析评价,并对其进行等值化,随后进行结构分类,建立题库.题库建成后,它除了能够更好指导我们命制高质量的试题,还将极大地节省命题组织成本和专家成本,同时保障考试的公平性和安全性.而计算机化测试的蓬勃发展,更将使题库的安全性、公正性、公平性和组织便利性得到质的提高.[1,4]

2.计算机化自适应考试

计算机化自适应考试(Computerized Adaptive Testing),又叫量身定制式测试(Tailored Testing),指的是根据测量学理论编写计算机程序,在考生答完一道题之后,根据考生的作答情况重新估计考生能力,再根据特定的选题原则选择最匹配的题目继续测验,直到达到终止规则为止.[4,6]项目反应理论中,对考生能力和对试题参数的估计,是计算机化自适应考试的理论基础之一.

3.与认知诊断理论的结合

认知诊断理论是上世纪开始兴起的一种新的测验理论,它关注的是考生的作答反应和其内部的认知结构特征之间的关系.[7]根据认知诊断理论,考生相同的得分并不意味着相同的学习水平,所以评价考生的能力和教师的教学效果应该根据考生作答的具体结果而不仅仅是分数.教师可以根据考生作答结果的不同,识别考生知识结构和解题策略,进行教学反思并改进教学实践.项目反应理论对认知诊断的发展有着很多应用,主要分为在构建认知诊断分类方法上和构建新的认知诊断模型上的应用.[4]

六、结束语

运用项目反应理论对各种考试进行分析评价,具有传统理论所不具备的优越性,但其理论较为艰深,数据计算也比较繁杂.所幸的是,现在已经有了诸如BILOGMG,PARSCALE 等软件,我们只需要学习一下基本的操作,就可以对数据进行分析解读,这为项目反应理论的普及和推广带来了很大的便利.教育者们可以利用它们得到试题的参数信息和考生的能力信息,以便于指导教育教学实践和试题命制评价,还可以把一些优质的试题项目进行积累,为未来大规模题库的建设等打下基础.