旋转稳定二维修正弹鸭舵法向力计算模型研究
2019-07-12王良明杨志伟
钟 阳,王良明,李 岩,杨志伟
(南京理工大学 能源与动力工程学院,江苏 南京 210094)
20世纪90年代,美国陆军装备研发中心提出了低成本强力弹药计划。二维修正引信具有纵向横向修正能力,精度高、成本低和对常规库存弹药兼容性好等优点,受到各国青睐,成为当前的研究热点,其中采用固定鸭舵式的精确制导组件(precise guidance kit,PGK)最为经典和成功。
气动特性技术是固定鸭舵二维修正弹的关键技术之一。常规弹药改装修正组件后,其气动特性必然发生改变,飞行过程中存在失稳现象,气动特性是首先要考虑的问题[1]。吴萍采用实验手段对弹丸的气动特性展开研究[2];徐辉雯等人仿真分析了二维修正弹修正组件反旋与不旋时气动特性的差异[3];程杰通过对有攻角和有舵偏角2种状态的分析,建立了基于2种状态叠加的气动力工程模型[4];美国陆军研究所的Sahu和Silton等人长期从事修正弹的气动特性数值计算,其数值计算结果与大量实验结果吻合较好,这也说明了CFD技术在获取弹丸气动力方面的可靠性。随着对修正弹气动特性研究的深入,其越来越细化,不仅对整弹气动参数进行计算,近来,还针对关键性气动部件鸭舵展开气动特性研究。Sahu等人[5]采用数值仿真计算了鸭舵产生的滚转力矩特性并将其应用于弹丸的滚转控制中;Silton等人[6-7]通过静态扫描模拟技术,数值计算了×型布局下,各片鸭舵产生的俯仰力矩随攻角的变化历程;彭程[8]采用CFD动网格技术研究了带鸭舵弹丸锥形运动和自转运动耦合作用下的空气动力学特性,分析了鸭舵诱导涡系结构的复杂发展情况以及周期性且有规律的气动力。含鸭舵的控制组件作为区别一般弹丸和二维修正弹的重要标志,也是二维修正弹最关键的气动部件,差动舵产生的轴向力矩决定着控制组件的转动情况,控制舵产生的法向力矩决定着弹丸飞行姿态,而以上2种力矩均可由鸭舵法向力近似计算获取。有必要建立一个较为精确的、满足控制组件转动或者不转动的适合旋转稳定二维修正弹的鸭舵法向力模型。基于此,本文针对之前工作的不足,采用多元泰勒展开理论,并对参数进行分析,建立关于弹丸攻角和舵偏角的二元鸭舵法向力计算模型。通过建立鸭舵坐标系,并考虑弹丸运动和迎风区背风区的影响,将模型扩展为适合于动态控制组件下的动态鸭舵法向力计算模型。为旋转稳定二维修正弹控制组件的滚转空气动力矩计算和全弹气动力计算提供参考。
1 鸭舵法向力模型
旋转稳定二维修正弹是通过调整控制组件的转动情况,由一对反向差动舵和一对同向控制舵产生期望的俯仰操纵力矩和偏航操纵力矩来控制弹丸姿态,从而达到弹道修正的目的。鸭舵作为控制组件上的关键气动部件,有必要研究其气动特性。其中,法向力能够产生使控制组件转动的轴向力矩,同时其产生的法向力矩也是弹丸俯仰操纵力矩和偏航操纵力矩的重要组成部分,因此,本节对鸭舵法向力展开研究,以期建立较为准确的计算模型。
1.1 鸭舵垂直于攻角面时的法向力模型
对于0°滚转角下的法向力模型,前人做过一些研究,文献[9]将攻角和舵偏角作为合攻角,以合攻角为参数,采用四阶多项式来表示弹翼法向力系数,考虑到攻角和舵偏角的耦合作用,模型中引入了2个相关系数;文献[4]将鸭舵法向力系数看作是0°攻角和0°舵偏角2种情况下的叠加,并基于该思想建立了工程气动模型。本节基于多元泰勒展开理论,考虑攻角和舵偏角的因素,并通过分析,对相关系数进行取舍,建立鸭舵垂直于攻角面时的法向力系数模型。
气动力计算采用的坐标系OAxAyAzA如图1所示,原点OA在弹丸质心处,OAxA轴与弹轴重合,沿弹尾指向弹头为正;OAyA轴在攻角平面内向上为正;OAzA轴满足右手法则。
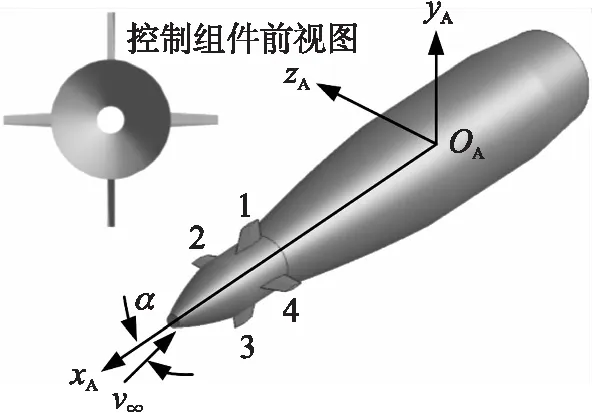
图1 气动坐标系示意图
图2为控制组件从弹尾指向弹头方向的视图。
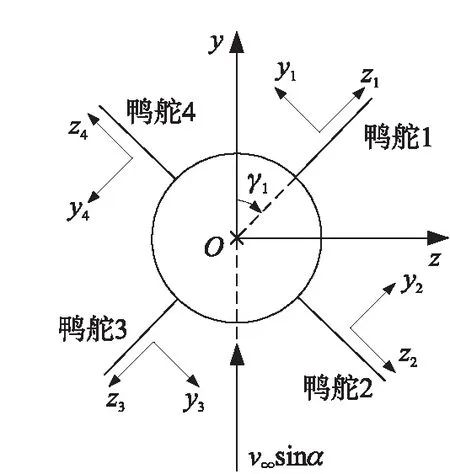
图2 控制组件后视图及鸭舵坐标系示意图
鸭舵坐标系是与鸭舵固连的坐标系,定义鸭舵i(i=1,2,3,4)坐标系Oxiyizi,Oxi轴与弹轴重合,由弹尾指向弹头为正;Ozi轴过鸭舵形心并与弹轴相交,由翼根指向翼稍为正,交点O为原点;Oyi轴满足右手法则。Oyi轴绕Oxi轴正向转到鸭舵i坐标系中Ozi轴时,转过的角度为鸭舵i的滚转角γi(i=1,2,3,4),控制组件的滚转角与鸭舵1相等。
在给定空气来流的马赫数和雷诺数条件下,忽略舵片之间的相互干扰,静态鸭舵法向力主要与弹丸攻角、舵偏角以及控制组件滚转角有关。本节讨论当控制组件不滚转且滚转角为0°,即一对控制舵垂直于总攻角面时,鸭舵对弹丸产生的法向力。此时,操纵鸭舵的法向力可视为舵偏角和弹丸攻角的二元函数,则鸭舵法向力系数为
CN=f(α,δ)
(1)
式中:α为弹丸攻角,δ为舵偏角。假设式(1)在点(0,0)的某邻域内具有n+1阶连续偏导数,采用泰勒展开:

(2)
式中:0<θ<1。考虑到非线性的影响,将式(2)保留到三阶,且有弹丸攻角和舵偏角都为0°时,鸭舵不产生法向力,即f(0,0)=0。重写式(2),有:

(3)
式中:下标α和δ均表示函数f对其求偏导。考虑到:①当弹丸攻角为0°时,大小相等且方向相反的舵偏角产生的法向力也必然大小相等且方向相反,即式(3)有f(0,δ)=-f(0,-δ),得fδδ(0,0)=0;②同理,当舵偏角为0°时,大小相等且方向相反的弹丸攻角产生的法向力也必然大小相等且方向相反,即式(3)也有f(α,0)=-f(-α,0),得fαα(0,0)=0;③当弹体攻角和舵偏角在保持大小不变的情况下同时反向,则法向力大小不变,方向反向,即式(3)有f(α,δ)=-f(-α,-δ),再综合①和②可得fαδ(0,0)=0。
通过以上分析,并令:
(4)
将式(4)代入式(3)有:
(5)
式(5)为控制组件滚转角为0°时,控制鸭舵法向力系数关于弹丸总攻角和舵偏角的非线性模型。该模型中包含有攻角和舵偏角的线性、非线性项及交叉干扰项。各系数的获取方法采用多元线性回归,将模型(5)写成一般多元线性回归形式:
(6)
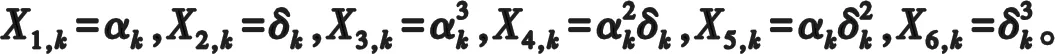
对于固定鸭舵二维修正弹,舵偏角可视为常量,令δ=δi,式(5)可写为
CN(α,δ)|γF=0,δ=δi=k0+k1α+k2α2+k3α3
(7)

1.2 动态任意滚转角下的鸭舵法向力模型
上节建立了当鸭舵垂直于攻角面时,其关于攻角和舵偏角的法向力系数模型。当鸭舵处于任意滚转角时,其法向力系数的获取方法通常是先得到有效攻角,然后把问题转化到0°滚转角下解决。本文借鉴该思想,并考虑弹丸运动和迎风区背风区等因素,建立动态任意滚转角下的鸭舵法向力模型。首先对鸭舵坐标系下的舵偏角和有效攻角进行说明。
图3为某鸭舵在其鸭舵坐标系中的姿态,当该鸭舵沿Oxi轴正向运动时,产生的空气动力在Oyi轴分量为负,此时舵偏角δi为负,反之则δi为正。
图4中vri为鸭舵i压心在鸭舵系下相对于空气的速度矢量,αe,i为鸭舵i的有效攻角。法向力的大小和方向主要取决于空气与鸭舵压心的相对速度矢量。

图3 鸭舵系下舵偏角示意图
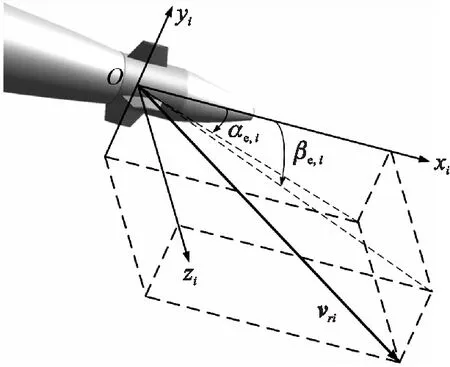
图4 鸭舵i坐标系及相关角度示意图
图5中rGC为弹丸质心位置G到鸭舵压心位置C的矢径,rGCA为矢径rGC在弹轴上的投影,rGCN为鸭舵压心C到弹轴的距离。鸭舵压心一般在鸭舵形心附近。当鸭舵i滚转角为γi时,质心到鸭舵i压心矢径为rGCi=(rGCAirGCNicosγirGCNisinγi)T。

图5 弹丸质心与鸭舵压心位置关系示意图
鸭舵i压心速度在气动坐标系OAxAyAzA下有矢量关系式:
(8)
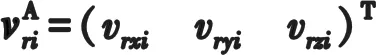
OAxAyAzA坐标系向鸭舵i坐标系的转换矩阵为
(9)
则鸭舵压心速度矢量在鸭舵系中的映射为
(10)
式中:vri=(vxivyivzi)T。鸭舵i有效攻角αe,i满足关系:
αe,i(γi,ωFx,ωy,ωz)=arctan(-vyi/vxi)
(11)
在有攻角的情况下,空气绕流受到弹体的影响,存在迎风压缩区和背风膨胀分离区,不同区域对鸭舵提供法向力的效率不同,通常迎风区效率高,背风区效率低。文献[9]数值计算了翼片在滚转角为0°时,即强度最高背风区时翼片法向力效率损失随攻角的变化曲线;滚转角为180°时,即强度最高迎风区利用牛顿流理论构造了压缩增效函数。二维修正弹的鸭舵在滚转过程中会周期性处在迎风区和背风区,为了使得法向力模型能够反映出迎风区和背风区的周期性影响,需要引入具有周期性的鸭舵效率模型。在鸭舵i坐标系中,αe,i为有效攻角,则βe,i=arctan(vzi/vxi)可相应称之为鸭舵i的有效偏角。随着控制组件周期性自转,有效偏角呈周期性变化,当有效偏角为正时鸭舵处于迎风区,否则鸭舵处于背风区。则可利用有效偏角来构造鸭舵效率函数:
(12)
式中:ke为鸭舵效率函数,kde和kie分别为背风减效因子和迎风增效因子,其大小与βe相关。不妨将kde在βe=0附近进行二阶泰勒展开:
(13)
当βe=0时,易知鸭舵不处于迎风区和背风区,鸭舵效率不提高也不减小,因此kde(0)=0。同理对减效因子kie进行类似处理,于是式(12)可写为
(14)
得到修正后的鸭舵坐标系下的法向力系数模型:
CNM=ke(βe)CN(αe,δ)
(15)
通过转换矩阵L-1(γ-π/2)和鸭舵系下的法向合力系数CNM=(0CNM0)T便可得到计算气动力坐标系OAxAyAzA下的动态鸭舵法向力系数模型:
(16)
2 数值仿真验证与分析
数值仿真采用有限体积法离散Navier-Stokes方程组,对流通量计算格式为SLAU2,粘性通量采用中心差分格式;湍流模型采用标准可压Spalart-Allmaras(S-A)模型。几何模型如图1所示,鸭舵1和鸭舵3为反向差动舵,舵偏角为4°,鸭舵2和鸭舵4为同向控制舵,舵偏角为8°。采用结构网格对流场进行划分;远场边界和近壁层网格设置参考文献[10];二维修正弹的运动采用人工滑移边界模拟。网格细节见图6和图7,网格总数约350万。

图6 流场网格剖面

图7 滑移网格结构
本文通过对比数值计算方法和飞行试验方法获取的控制组件转速来间接说明本文所采用的数值方法的可信度。本文研究对象在控制组件自由滚转的条件下进行了飞行试验。通过飞行过程中获取的弹身转速和控制组件相对弹身的转速,处理出控制组件的绝对转速ωFx。
图8中,通过对比数值方法[11]处理出的控制组件平衡转速和飞行试验获得的转速,其变化规律大致相同,各数值计算点和试验数据吻合较好,误差小于15%。控制组件的滚转空气动力矩主要是由鸭舵法向力产生的,说明通过本文数值方法得到的鸭舵法向力是合理的,计算结果具有参考价值。本文采用该数值方法对鸭舵法向力模型的合理有效性加以验证分析。
验证分为两部分:第一部分,采用定常CFD方法仿真验证模型(5),能够预测不同攻角和舵偏角下的鸭舵法向力;第二部分,采用非定常CFD方法仿真验证控制组件滚转条件下动态鸭舵法向力模型(16),能够预测出每一片鸭舵法向力规律。
模型(5)中参数采用定常流场计算结果进行拟合。通过网格旋转,舵偏角可以为±4°、±8°。定常流场工况:马赫数2.0,压力101 325 Pa,温度288.15 K,密度1.225 kg/m3;攻角和舵偏角组合见图9中数值计算点。为了拟合模型(5)中的系数,从数值计算的单片鸭舵法向力系数中选取19个不同攻角和舵偏角组合,如表1所示。

图8 控制组件转速随马赫数的变化关系
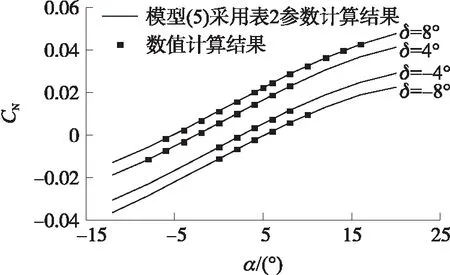
图9 不同舵偏角下法向力系数随攻角的变化关系

编号δ/(°)α/(°)CN18-6-1.838 7×10-328-42.405 2×10-338-26.738 0×10-34801.113 8×10-25821.558 8×10-26842.004 5×10-27852.225 5×10-28862.442 5×10-29882.863 3×10-2108103.246 0×10-211812-1.149 4×10-2124-8-7.404 9×10-3134-6-3.153 4×10-3144-41.195 2×10-315405.584 3×10-316429.969 4×10-317441.437 6×10-218461.873 9×10-219482.303 3×10-2
利用表1中的参数,通过式(6)获得多元回归方程组,进而通过最小二乘拟合出模型(5)中各参数。在|α|≤12°,|δ|≤8°范围内,鸭舵法向力系数拟合结果相对数值计算值误差小于2.05%。拟合参数结果如表2所示。

表2 模型(5)参数拟合结果
从图9中可以看出,采用4°和8°舵偏角拟合出的系数,同样适用于-4°和-8°,即在定马赫数和雷诺数下,无需改变表2中的参数,模型(5)计算出的鸭舵法向力系数与数值计算出的不同攻角、不同舵偏角下的结果吻合得很好,反映出本文针对弹丸攻角和舵偏角所建立的二元鸭舵法向力模型是合理有效的。由图9中“δ=8°”曲线可以看出,当攻角约10°时开始出现非线性现象。将舵偏角为8°时的鸭舵附近流场作剖面,对流场进行观察。由图10可知,当攻角为10°时,空气在舵面发生了分离,与仿真曲线表现出的非线性相一致。

图10 舵偏角8°时不同攻角下空气流动情况
模型(16)中含有鸭舵效率模型(14),该模型中的相关参数采用定常流场计算结果拟合,工况为:鸭舵滚转角0°和180°,舵偏角8°,弹丸攻角0°、2°、4°、6°、8°,其余条件与之前相同。当滚转角为180°时,有效偏角βe与攻角相等;当滚转角为0°时,有效偏角βe为攻角相反数。
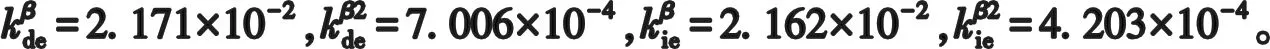
为了得到控制组件滚转时4个鸭舵对弹丸产生的法向力系数,采用滑移网格来模拟转动,非定常流场工况为:控制舵偏角大小为8°,差动舵偏角大小为4°;马赫数Ma=2.0;控制组件转速ωFx=-100 rad/s;攻角α=2°,5°。双时间步收敛精度为0.01,内层最大迭代100步,每个时间步转1°。
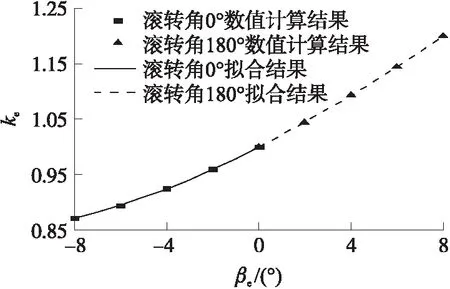
图11 迎风区背风区鸭舵效率随有效偏角关系曲线
图12中,从原点指向曲线上任意一点所成的矢量为鸭舵法向合力系数矢量,当控制组件以角速度ωFx=-100 rad/s滚转时,该矢量末端轨迹在面OAyAzA上形成周期性曲线,可称为法向力矢端轨迹线。图12中的轨迹线分别为CFD数值计算结果和模型(16)采用表2参数所计算出的结果。从图12(a)和图12(b)中CFD得到的鸭舵法向力矢端轨迹线可知,由于初始流场不精确,非定常数值计算结果初期不合理,但这种初始效应随着时间推进逐渐消失,最后形成周期性的曲线;从图12(a)和图12(b)还可以看出,鸭舵1和鸭舵3的轨迹线几乎一致,因为鸭舵1和鸭舵3只有相位上的差别,它们转到同一位置时的法向力一致;由于转动,鸭舵2在整个过程中的有效攻角是减小的,鸭舵4反之,从图12(a)可见鸭舵4的法向力系数曲线比鸭舵2整体大一圈;鸭舵2先进入背风区并产生OAzA轴负向的法向力分量,再进入迎风区并产生OAzA轴正向的法向力分量,因此正向分量绝对值比负向大,形成了非对称形状,鸭舵4则与之相反,这一点从图12(b)中可看出。通过上述分析可知,非定常数值计算结果反映出的特性是合理的。
另外,由图12(a)和图12(b)攻角与舵偏角的关系大致来看,当攻角大于舵偏角时,轨迹线为双环形,如图12(b)鸭舵1。此时,整个法向力矢端轨迹线几乎都在OAyA轴正向,即无论控制组件如何转动,鸭舵几乎都不能产生OAyA轴负向的力;当攻角与舵偏角相当时,轨迹为苹果型,如图12(a)鸭舵1和图12(b)鸭舵2。此时,鸭舵不仅能够产生正向的力,也能够产生较小负向的力;当舵偏角大于攻角时,轨迹为单环型,如图12(a)鸭舵2。此时,鸭舵能向各个方向提供较大的法向力。为了鸭舵能提供足够的法向力,一种是增大鸭舵的气动面积,另一种是增加舵偏角。基于本文的分析,更倾向于在不发生分离的情况下尽量选择大舵偏角,这样更有可能为弹丸提供各个方向较大的法向力,提高鸭舵利用率。

图12 不同攻角下法向力系数矢端轨迹线
对比图12中数值和模型计算结果可以看出,动态鸭舵法向力模型(16)在来流条件一定的情况下,仅采用一组系数便能预测出控制组件滚转过程中不同攻角下每片鸭舵上的法向力系数,预测结果与数值计算结果基本吻合,说明本文提出的模型是合理有效的。
3 结束语
本文针对旋转稳定二维弹道修正弹,基于多元泰勒展开理论,并对系数进行分析取舍,得到鸭舵垂直于攻角面时,其关于攻角和舵偏角的二元法向力模型。考虑到在实际飞行中,控制组件会发生滚转,且鸭舵会交替出现在迎风区和背风区,通过建立鸭舵坐标系和加入鸭舵效率模型,进一步将该模型扩展为动态鸭舵法向力模型。最后通过数值仿真验证了该模型的合理性,为旋转稳定二维修正弹的设计提供参考。
