基于随机鲁棒优化的导弹姿态控制系统设计

徐 帅,高 敏,方 丹,王 毅,赵文栋

(1.陆军工程大学 石家庄校区,河北 石家庄 050003;2.中国人民解放军61267部队,北京 100000)

导弹姿态控制系统(后文简称“姿控系统”)是导弹总体设计的重要组成部分,控制参数的设计与整定水平决定了姿控系统的控制品质。基于经典频域设计法的姿控系统以其结构简单、容易工程实现、控制性能满足现代战争对武器性能的需求等优势获得广泛应用。

在传统控制律设计中,为满足导弹的全包线飞行要求,一般采用增益调度法,该方法需要在每个特征点处逐一调节控制律增益系数,故要求设计者具有相当的经验及技巧。

为避免人工调参的劣势,将具有多种性能指标要求的控制问题转化为一个多目标优化问题,采用带约束的多目标优化方法来解决是一种有效思路。然而,常见的运用多目标优化方法设计姿控系统的方案大多采用了特征点处导弹弹体的标称模型,而基于风洞或仿真试验数据搭建的标称模型只能近似地描述控制对象。导弹在实际飞行过程中,弹体实际模型会发生变动[1],这使得实际模型与标称模型之间存在偏差,因此,根据标称模型设计并获得的系统性能在实际飞行环境中不一定能保持。针对实际工程应用中导弹参数变化会引起系统稳定裕度等鲁棒性能指标下降,甚至系统失稳的情况,本文引入随机鲁棒分析与设计方法进行导弹姿控系统设计,提高设计效率的同时,改善系统应对时变参数的能力。

随机鲁棒设计是一种基于数理统计和现代优化算法的鲁棒控制设计方法。该方法利用蒙特卡洛仿真在各种摄动状态下检验控制系统响应,统计各种摄动状态下系统稳定性及各性能指标的不满足概率,并对稳定性和各性能指标不满足概率适当加权,建立随机鲁棒适应度函数,通过现代优化算法在参数可行域内搜索符合控制指标约束的一组最优参数,使闭环系统的性能指标满足概率最优化,已成功应用在各种控制系统设计中。Polyaka等人[2]将随机鲁棒与LQR相结合设计控制律;Horn等人[3]运用随机鲁棒方法进行直升机内环控制律设计;谭毅伦等人[4]提出了随机鲁棒变结构控制方案,设计了高超音速飞行器纵向通道变结构控制律;孙佳星等人[5]结合随机鲁棒和拉丁超立方抽样法,提出一种无人机自主着舰控制律。

本文针对导弹姿控系统待设计控制参数多、性能指标要求高的特点,运用随机鲁棒方法进行了鲁棒姿控系统的设计。对比仿真表明,与仅使用粒子群算法优化设计的控制器相比,随机鲁棒控制器可有效提高导弹对飞行过程中参数摄动的适应性。

1 导弹姿态控制系统数学模型

导弹姿控系统由弹体动力学环节、敏感元件(速率陀螺以及惯性组件)、控制器(动、静态增益及校正网络)以及执行机构等组成。本文以俯仰通道为被控对象设计PD控制器,并对其传递函数参数进行整定。俯仰通道的姿控系统结构框图如图1所示。

图1中,姿控系统设计为两回路,反馈俯仰角速率的阻尼回路为内回路,反馈俯仰角的控制回路为外回路。俯仰通道姿态控制律为

(1)

(2)

(3)

式中:T11～T14及T21～T23为时间常数;ξ11,ξ12,ξ21,ξ22为阻尼系数。

(4)

式中:KD为弹体传递系数,TqD为弹体气动时间常数,ξD为弹体相对阻尼系数,TD为弹体时间常数。

阻尼回路设计时,忽略速率陀螺和惯性组件的动态特性,即令Gδ(s)=1,Gg(s)=1,则简化后阻尼回路的闭环传递函数为

(5)

(6)

为了使研究思路清晰,先研究标称系统的优化,再讨论鲁棒系统优化问题。

2 姿控系统性能参数选择

优化过程需要性能指标来约束。导弹姿态控制系统要求响应快、超调小,在不确定因素干扰下能保持良好的稳定性和控制精度。姿控系统的快速性通过单位阶跃响应的上升时间和调节时间来保证,系统的稳定性和鲁棒性通过幅值裕度和相位裕度来保证。

从系统稳定性、时域和频域3个方面选定系统性能指标,如表1所示。

表1 俯仰回路稳定性与性能指标

3 标称姿控系统优化

将上节的性能指标体系转化为约束,定义目标函数,设置合理参数向量取值区间,采用合适的优化算法,在满足指标约束的条件下搜索使系统目标函数最小的参数向量,从而获得最优控制器。

本文中采用标准粒子群算法[6]进行参数寻优,目标函数即适应度函数,其目标函数定义为

(7)

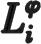
(8)

式中:R为充分大的正数。

优化流程如图2所示。

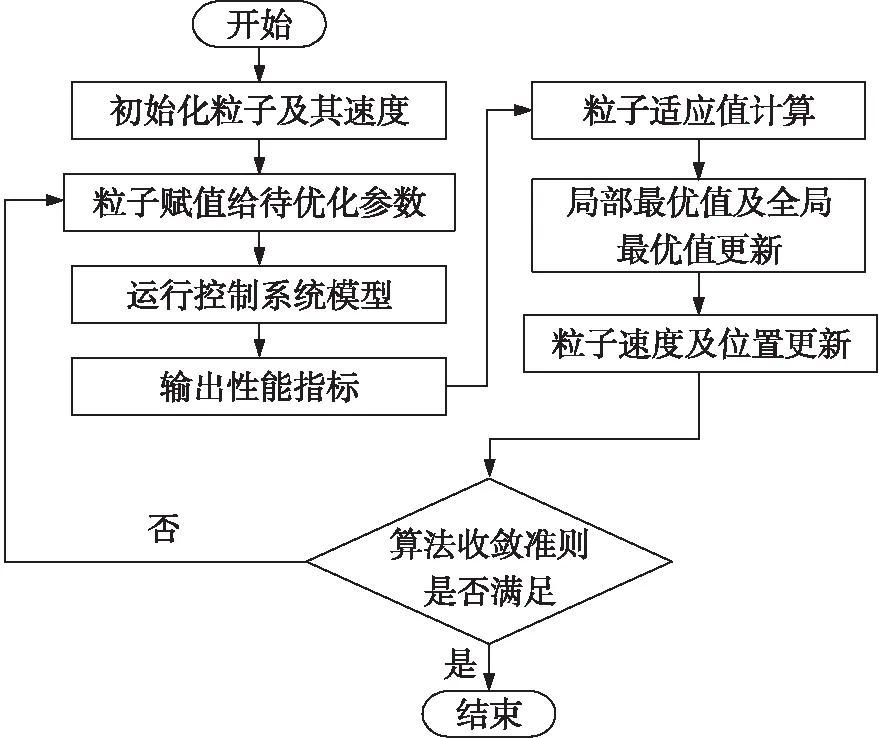
图2 标准粒子群寻优流程图

优化过程如下:PSO随机初始化粒子群,将该粒子群中的粒子依次赋值给控制器的待优化参数;运行控制系统模型,得到该组参数对应的性能指标,并传递到PSO中计算该粒子的适应值;对比新适应值与该粒子的个体最优值及粒子群的历史最优值,更新个体最优值及粒子群的历史最优值;更新粒子群的位置和速度,产生新的粒子群;判断是否满足退出算法的条件,若是,则终止算法,输出寻优结果,否则利用产生的新粒子继续寻优。

4 姿控系统的随机鲁棒优化

随机鲁棒方法将闭环控制系统某项设计指标的不满足概率作为系统关于该指标的鲁棒性度量。不满足概率是一种准确的度量,由闭环控制系统的蒙特卡洛仿真得到,其数值明确地反映了一个鲁棒设计能够容许的不确定性程度。随机鲁棒方法设计流程如图3所示。

图3 随机鲁棒设计流程图

成功获得闭环控制系统的稳定鲁棒性和性能鲁棒性度量(即各项设计指标的不满足概率)之后,即可在此基础上使用优化算法实现控制器的优化设计。在此,本文继续采用标准粒子群优化算法。

粒子群算法的目标函数定义为

(9)

在优化控制器参数时,按照“先内后外”的顺序逐层优化,先得到内回路控制器最优参数并固定后,再在此基础上设计外回路控制器参数。该方法可以保证控制器每一层具有期望的性能,降低寻优过程的复杂度。

采用随机鲁棒优化方法的具体设计过程如下:

①在选取的各特征点处,令导弹各动力学系数按正态分布进行摄动,模拟飞行过程中环境不确定性和参数不确定性;

②考虑内部稳定性并结合设计经验,设置待定控制参数向量的取值区间;

③进行蒙特卡洛仿真获得所有设计指标的不满足概率;

④使用粒子群优化算法对随机鲁棒目标函数进行优化,使目标函数最小的参数向量即为最终优化结果。

首先,依据设计指标提出一个包含系统稳定性、时域和频域指标的指标度量体系;其次,依据指标度量体系,基于蒙特卡洛仿真统计生成所有指标的不满足概率,并根据实际控制系统的性能要求,对各指标不满足概率适当加权定义适应度函数;最后,采用粒子群算法,根据适应度函数值在参数取值区间内对待定控制参数进行寻优。

5 仿真验证

为说明问题,本文仅以某一特征点的控制器设计为例验证随机鲁棒方法的有效性。在该特征点处的标称弹体传递函数参数分别为KD=-2.122 7,TD=0.048 3,ξD=0.101 5,TqD=0.563 4。考虑到外部气动参数的变化引起动力学系数ap(p=1,2,…,5)摄动,从而影响弹体传递函数参数,故设定ai(i=1,2,…,5)摄动幅度为±25%,并在摄动范围内进行1 000次蒙特卡洛仿真以考察所设计系统的鲁棒性。仿真中,粒子群算法的种群规模均为50,终止代数均为30代,采用线性递减惯性权重(wmax=0.9,wmin=0.2)。粒子中各变量取值区间依据先验值确定,设置如表2所示。

表2 待寻优参数取值区间

①标称系统优化结果。

由图可以看出,标称系统各性能指标满足设计要求。内外回路幅值裕度均大于15 dB,相位裕度均超过70 dB。阻尼回路的上升时间和调节时间均小于设计指标;控制回路无超调,响应快速平稳无逆返,上升时间优于设计值,调节时间小于设计指标0.7 s。

图4 阻尼回路稳定裕度

图5 阻尼回路单位阶跃响应

图6 控制回路稳定裕度

图7 控制回路单位阶跃响应

结合动力学系数摄动进行1 000次蒙特卡洛仿真,得到系统各性能指标散布特性,如图8～图12所示。图中,N为蒙特卡洛仿真次数。

由图可以看出,控制回路的各项指标受参数摄动影响后散布范围较大。幅值裕度变化幅度达到11 dB,相位裕度变化幅度达到41°,超调量变化幅度达到13.2%,上升时间变化幅度达到1.6 s,调节时间变化幅度达到3.7 s。同时观察到,标称系统受参数摄动影响后,性能变差的趋势明显。

图8 控制回路幅值裕度散布

图9 控制回路相位裕度散布

图10 控制回路上升时间散布

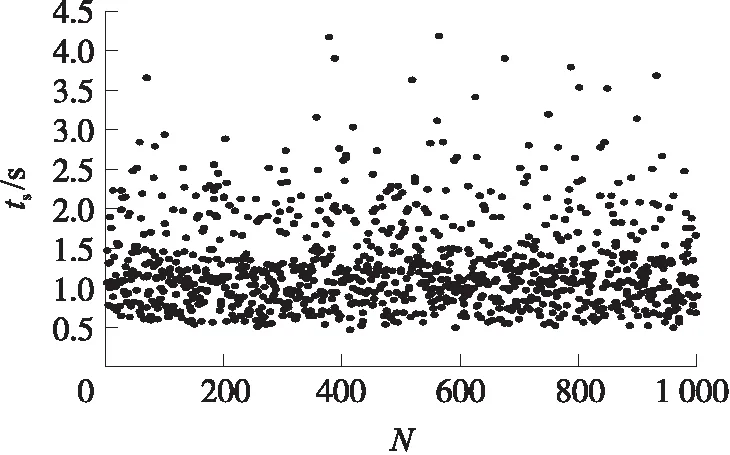
图11 控制回路调节时间散布

图12 控制回路超调量散布

②鲁棒系统优化结果。

图13 阻尼回路稳定裕度

图14 阻尼回路单位阶跃响应

图15 控制回路稳定裕度

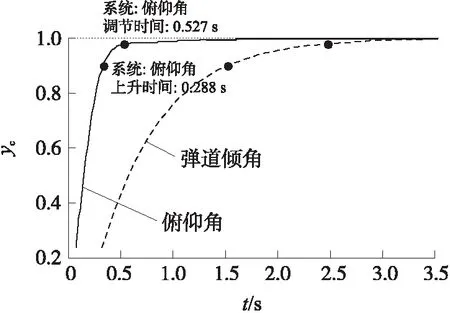
图16 控制回路单位阶跃响应

由图可以看出,随机鲁棒系统各性能指标满足设计要求。内外回路幅值裕度均超过15 dB,相位裕度均超过70 dB,且稳定裕度指标均优于标称系统。阻尼回路的上升时间和调节时间均小于设计指标,优于标称系统;控制回路无超调,响应快速平稳无逆返,上升时间和调节时间均优于设计值。与标称系统相比,鲁棒系统的上升时间和调节时间分别缩短了27.5%和21%,在保证稳定性的前提下,有效提高了系统的响应速度,且稳定裕度也更好,说明“先内后外”的寻优顺序比内外回路同步寻优更能有效获得最优解或次优解。

结合动力学系数摄动进行1 000次蒙特卡洛仿真,得到系统各性能指标散布特性,如图17～图21所示。

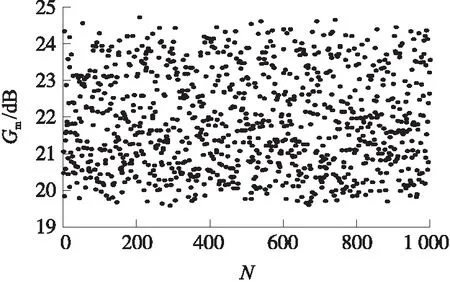
图17 控制回路幅值裕度散布

图18 控制回路相位裕度散布

图19 控制回路上升时间散布

由图可以看出,控制回路的各项指标受参数摄动影响后散布范围较大。幅值裕度变化幅度小于6 dB,相位裕度变化幅度为32°,超调量变化幅度为8%,上升时间变化幅度不到1.1 s,调节时间变化幅度为3.2 s。与标称系统相比,鲁棒系统受参数摄动影响小一些,尤其是幅值裕度的散布情况,鲁棒系统明显优于标称系统。

图20 控制回路调节时间散布

图21 控制回路超调量散布

计算各性能指标散布的均值和标准差,如表3所示。

表3 各性能指标散布的均值和标准差

由表3可以看出,除阻尼回路上升时间指标相近外,鲁棒系统其他指标的均值和标准差都比标称系统有所改善。尤其是控制回路的时域指标提升比较明显,不仅上升时间均值缩短了29.5%,同时超调量均值也减小了55.3%,相应地,调节时间也下降了27.8%,这样随机鲁棒系统在参数摄动条件下可更快更平稳地响应控制指令,大大提高了控制效果。在同样强度的随机参数摄动情况下,随机鲁棒系统的稳定裕度指标更好,散布也更小。由以上分析可得,随机鲁棒方法可有效提高系统抑制参数摄动影响的能力,更好地保持系统稳定性和快速性。

6 结束语

本文针对多目标优化方法设计控制系统过程中考虑系统鲁棒性较少的问题,运用随机鲁棒优化方法整定导弹姿态控制系统参数,有效提高了系统鲁棒性。该方法采用粒子群算法对控制参数自动寻优,搜索得到满足性能指标的最优参数或次优参数,降低了参数整定的难度;优化算法收敛速度较快,具有良好的全局搜索能力,是一种有效的参数整定方法。蒙特卡洛仿真结果表明,该优化方法所设计姿控系统的综合性能,尤其是鲁棒性,优于常规的多目标优化方法得到的系统性能,可在导弹姿控系统设计中推广应用。