基于Arnold变换和DRPE技术的 数字音频信号加密方案

刘效勇，卢佩，史芹，邵建新，张永才，孙迪

(1石河子大学理学院，新疆 石河子832003； 2石河子大学信息科学与技术学院，新疆 石河子832003；3石河子大学师范学院，新疆 石河子832003)

随着计算机网络及通信技术的迅猛发展，数字音频信息可以方便快捷地被传输和发布，音频的各种应用也越来越向智能化、移动化和安全化发展。人们不仅关注音频信息传输的质量，而且更加注重传输过程中信息的完整性、保密性和安全性。信息安全关系着个人隐私、商业机密乃至国家安全等诸多方面，因此，研究音频加密具有重大的实际意义，也是现代通信技术中的重要部分。数字音频具有精细、准确、容量大等特点。Tang S等[1]使用AES算法对音频信号进行了加密，不过在密钥扩展过程中容易受到密码攻击；Gambhir A等[2]通过DES算法和RSA算法相结合实现了语音信息加密，但由于采用以数学方法为主的传统加密算法，编码和解码速度慢，造成效率低下，不能满足实时性要求；Li G等[3]通过控制混沌维度设计出音频加密系统，加密效果好，但由于采用低维混沌系统导致密钥空间小，安全性降低；Lima J B等[4]应用图像作为可变密钥进行音频加密，但可控性不强，鲁棒性不高。

为增加保密安全性，一些音频加密方案采用了多重加密机制，虽然增加了密钥空间，提升了加密鲁棒性，但同时也增加了数据处理量和加解密处理速度[5]。同时，大部分音频加密方案验证安全性时方法不统一，采用主观评判标准时人为因素影响过大，而采用客观评判方法时过于复杂的弊端[6]，因此，相关研究在效果测试时大多采用客观评价标准中的部分参量进行对比分析。

本文提出一种将图像加密思想应用到音频信号的安全方案，先将一维数字音频信息转化为二维图像形式，此处称为“声图(Sound figure)”，再使用图像编码的方式实现对音频信息编码，以提高加密速度，并借助Arnold变换和双随机相位编码(DRPE)技术完成对音频加密，采用无理数序列构建随机相位板，以增强加密安全性和效率，同时，这种转换为声图的方式也可以有效解决进行密文鲁棒性判断时主、客观判断方法存在的弊端。

1 理论基础

1.1 Arnold变换

Arnold变换也称猫脸变换，是1968年数学家V I Arnold研究遍历理论时提出的[7]，变换有一维、二维、多维多种形式。一维Arnold变换可定义如下：坐标为(x,y)的一点经变换到另一点后坐标变为(x′,y′)，则有：

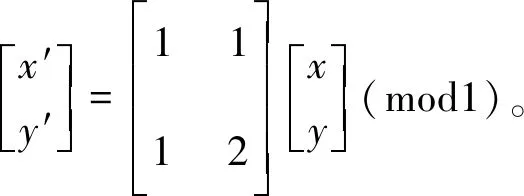
(1)

图像属于二维信息，假如尺寸为N×N的原始图像像素坐标为(x,y)，Arnold变换以后的像素坐标为(x′,y′)，二维Arnold变换的表达式为：

(2)

可以得到迭代公式：

(3)

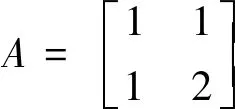
Arnold变换是在变换域实现数字图像加密的一种主要技术，利用该变换对图像像素进行置乱，能够将有意义的数字图像变成像白噪声一样的无意义图像，从而实现信息的隐藏，并且将置乱次数作为安全密钥，从而增强系统的安全性和可操作性。Arnold变换算法简单、效率高、速度快，系统开销小，在信息安全领域经常使用[8-10]。

1.2 双随机相位编码技术

双随机相位编码技术是1995年由美国康涅狄格大学的Refregier和Javidi教授提出的，这种技术采用4f光学信息处理系统实现[11-12]。

如图1所示，在图像的加密过程中，起加密密钥作用的是2个随机相位掩模板RPM1和RPM2，可用下式表示：

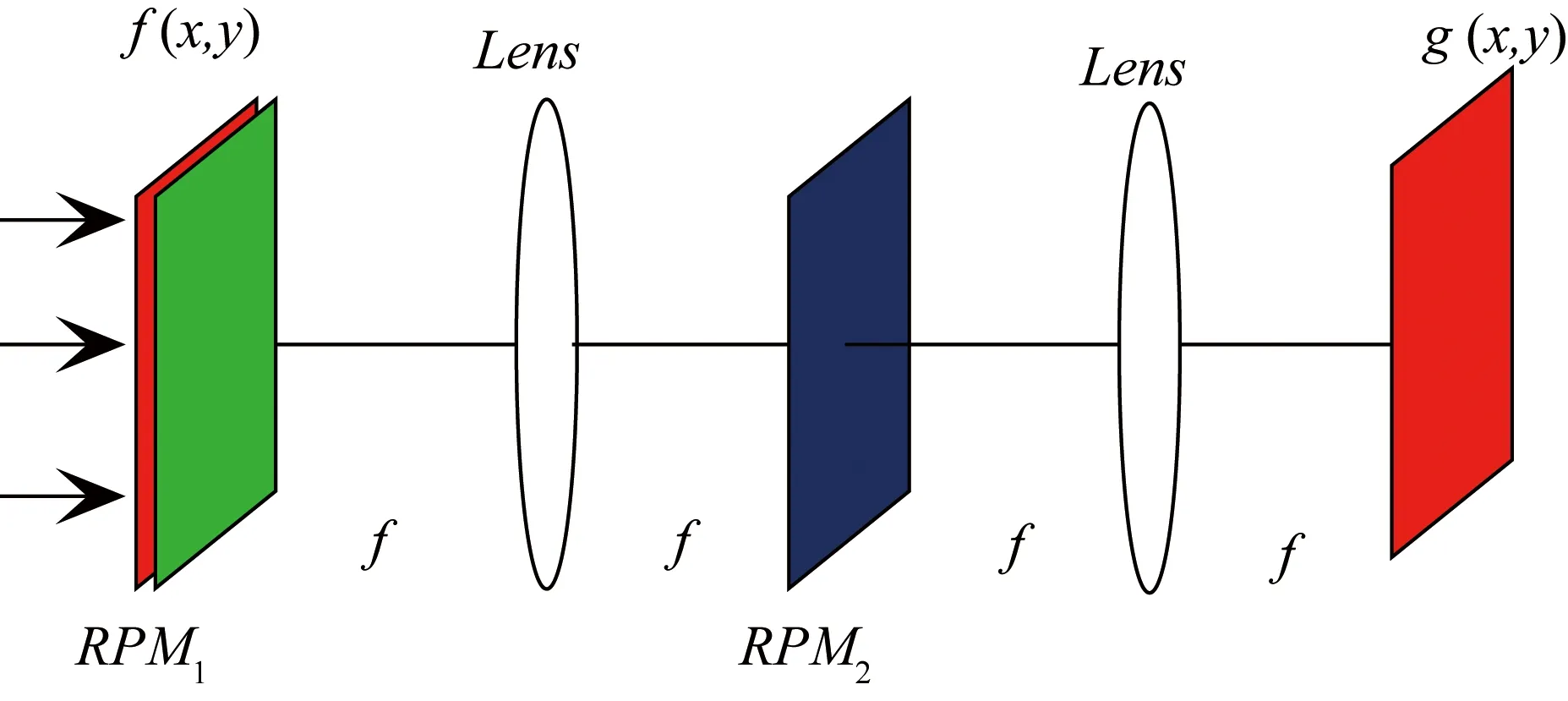
图1 基于4f系统的双随机相位编码系统Fig.1 4f systems based on double random phase encoding

θ(x,y)=exp[i2πθ0(x,y)],

(4)

φ(u,v)=exp[i2πφ0(u,v)],

(5)

其中:(x,y)、(u,v)分别代表空域和频域坐标，θ0(x,y)、φ0(u,v)代表空间域和频域均匀几率分布在[0,1]区间的随机相位函数，二者能够对输入的光产生0～2π的随机相位延迟。

双随机相位编码光学系统的加密与解密过程用数学表示如下：

g(x,y)=FT{FT[f(x,y)·θ(x,y)]·φ(u,v)}，

(6)

f(x,y)=FT-1{FT-1{g(x,y)}·φ*(u,v)}·

θ*(x,y)，

(7)

其中：f(x,y)为输入图像，g(x,y)为加密图像，FT、FT-1分别表示傅里叶变换和傅里叶逆变换，“*”表示共轭。

加密过程中采用随机相位掩模板作为密钥，因此密钥空间非常大，在不确定密钥相位分布的前提下，利用反卷积运算破解是不可能获得成功的。此外，由于随机相位掩模板纯粹是相位信息，完全不能使用光强探测器接收它的相位分布，因此，对这种方式编码的加密攻击也极难破译，加密的稳健性和安全性极高。

1.3 基于无理数的随机相位掩模板设计

在序列密码领域，通常采用序列构建函数生成随机序列作为密钥，但序列构建函数存在周期性，从而对信息的安全造成威胁。由于无理数是无限不循环小数，周期无限长，无理数序列的随机性、自相关性、功率谱和最大Lyapunov指数表明其具有很好的似混沌特点，将其构造成随机的相位掩模板作为密钥，能够提高破译的难度，有效保证信息的安全性，因此，本文使用无理数展开式构造随机相位掩模板作为加密密钥。

(8)

由序列可生成满足μ(0-1)均匀分布的随机相位板，表1为随机相位板生成方式。

表1 随机相位板设计Tab.1 Random phase plate design

2 加解密方案

2.1 数字音频信息转换成声图

音频信息可看作是一维的(图2a)，用Z(K)[13]表示，即

[Z(1),…,…,…,Z(K)],

(9)

其中Z(1)、Z(2)、…、Z(K)表示数据中的每个采样。

用f(M,N)表示二维矩阵，它的大小是M×N像素，表示为：

(10)

将音频信息赋值到二维数组中，赋值的表达式为：

f(m,n)=Z((m-1)*M+n)，

(11)

式(1)中1≤m≤M，1≤n≤N。

赋值后二维数组变为

(12)

赋值后的二维数组表现为图像的形式，将其称为声图(图2b)。

图2 音频信号转化为声图Fig.2 Digital audio transformed into Sound figure

由图2可以看出：

(1)转换成声图后的数字音频信息具有图像的特性，但没有可读性，通过声图得不到任何有用信息。

(2)声图中每个像素值对应数字音频的每个采样单元，声图越大容纳的数字音频信息量越大，如一幅1024×1024像素的声图可以容纳131 s 8000 Hz采样频率的单声道数字音频信息。

2.2 声图的加密

加密过程中选择声图的像素为256×256，首先使用Arnold变换将声图加密一次，为了提高安全性，然后再使用双随机相位编码技术进行二次加密。图3为数字音频信息的加密流程图。

为提高信息保密安全性，将声图分成16个64×64像素的小块，分别对每个小块做Arnold变换，每个分块的变换次数为10次。如图4b所示，声图经过Arnold变换后已变得随机和混乱。

然后使用双随机相位编码技术对经过Arnold变换后的声图加密，随机相位板使用无理数序列来构建。对声图编码后的密文图像表现形式为噪声(图4c)所示，原始音频信息转换为图像形式后已被很好的隐藏。

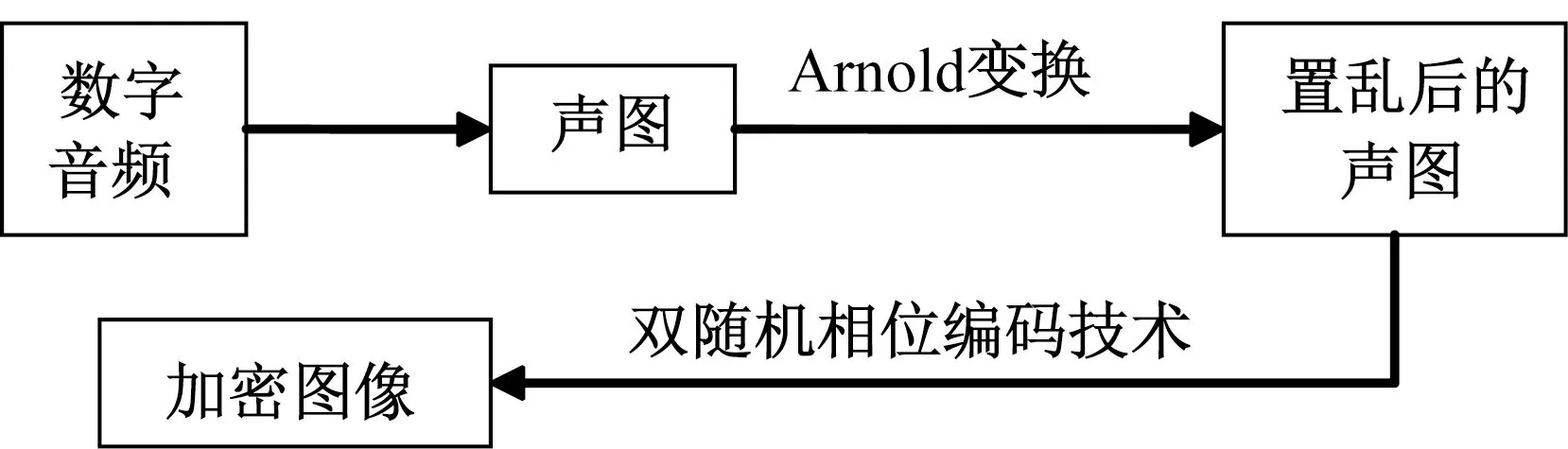
图3 加密流程图Fig.3 Flow chart of encryption

2.3 数字音频的解密过程

解码过程是编码过程的反过程，解码时密文图像首先通过逆向双随机相位编码技术，然后再通过反向猫脸变换解密为声图，最后声图转化为数字音频信息。

解码过程中以声图分块大小、猫脸变换次数和使用无理数序列构建随机相位板的信息作为解码的密钥使用。

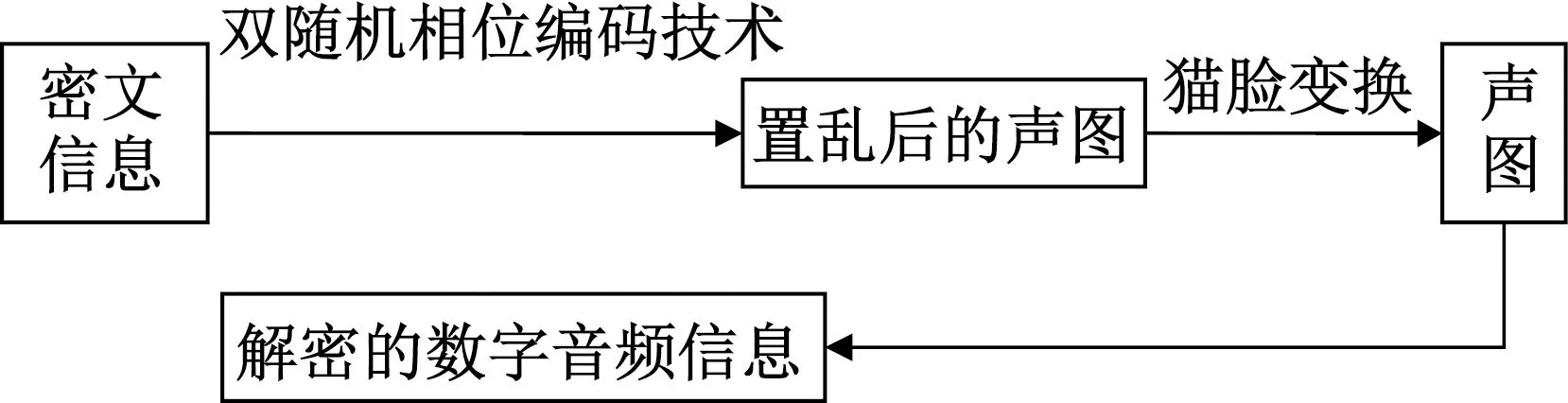
图5 解密流程图Fig.5 Flow chart of decryption

使用该加密方案编码数字音频信息时，数字音频信息首先变换成为声图，声图经过猫脸变换和双随机相位编码技术两次编码，解码信息有很好的质量(图6b)。

3 加密效果和安全性分析

实验中使用的是8000 Hz采样频率，采样单元8位量化的数字音频信息。声图采用256×256像素。为了测量解密信息的质量，采用信噪比(SNR)来描述解密的信息与原始信息之间的差异，其定义如下：

(13)

式(13)中:K是数字音频总的采样数，Zin和Zout分别表示原始数字音频和解密后的数字音频。

3.1 加密效果分析

3.1.1 密钥敏感性与密钥空间分析

加密数字音频信息时密钥是Arnold变换次数和制作随机相位板的无理数及无理数展开的取位。实验中选取Arnold变换次数为10次，将无理数π展开，其中初始位置为2，小数位数为4，序列长度为256×256。如果使用错误密钥初始位置为3时，则解密结果变成图6c所示随机噪声，解密信息的平均信噪比为-8.2，人耳不能分辨出有效信息，因此，该加密方案具有很强的密钥敏感性。

在本该加密方案中，Arnold变换有2个模板参数，无理数序列展开有5个模板参数，理论上可以设置无穷多个密钥，假设使用精度为16位有效数字的计算机，则该加密方案的密钥空间为无穷大，因而能够有效抵抗穷举攻击。文献[1]密钥空间为1096,文献[2]的密钥空间为10195,文献[3]的密钥空间是1064,本加密方案和文献[1-3]比较密钥空间最大，安全性最高。

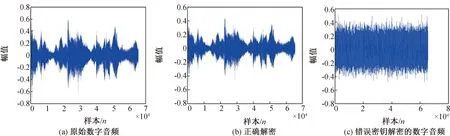
图6 解密结果Fig.6 Decryption result

3.1.2 相关性分析

随机抽取原始数字音频和对应密文各10000对相邻数据分别计算其相关性，结果(图7)显示：

(1)图7a为明文语音的相关性，相关系数为0.9672，可见是高度相关的。

(2)图7b为加密密文的相关性，相关系数为0.0616，说明密文相邻数据相关性很弱，原始信息的统计特征已被扩散至随机的加密密文之中。

图7 相关性对比图Fig.7 Contrast chart of correlation

3.1.3 直方图分析

统计分析是评判抗攻击能力优劣的重要标准。图8a为原始音频声图的直方图，图8b为密文的直方图。由图8可以看出：原始音频的数据值在某些点出现的频率很高，而加密后的直方图呈现类随机均匀分布，很好地掩盖了原始音频的数据值分布规则，因此这种加密掩盖了明文的统计特性，可以更好抵抗针对密文统计特性的破解攻击，增加破译难度。

3.1.4 加密耗时分析

在加密过程中，加密运行时间是一个重要因素，可以反映加密算法的优劣。选择3段大小不一的wav格式音频文件，用本文的加密方法和文献[2]以及文献[3]加密方法分别进行了3次加密操作，通过计算平均时间比较加密时长，测试结果见表2。由表2可知：

(1)虽然受计算机运行环境等因素影响，计算结果有一些偏差，但可以看出，本文加密方法较文献[2]耗时大有改善，与文献[3]相差不多，而且本文加密安全性较高。

(2)加密耗时也和各个加密方案中各个加密参数的选择有关。如果将本文无理数序列构建相位板时小数位数取为2，则耗时会明显减少，因此，对于不同加密方法各有优异，在选择时应该根据实际需要进行选择。

图8 直方图对比图Fig.8 Contrast chart of histogram

表2 算法加密耗时对比Tab.2 Time comparison of algorithm encryption

3.2 安全性和鲁棒性分析

3.2.1 密文遭到剪切攻击时解密信息的质量

来自外部的攻击不只局限在试图破译，也包括剪切密文信息，加入噪声或通过滤波器等主动攻击形式。在密文信息遭到剪切时，解密信息的质量会极大的降低，通过测量信噪比可以确定解密信息的质量降低情况，并确定密文信息容许的攻击程度。

当1/4的密文信息被剪切时，通过对大量密文信息测量，解密信息的平均信噪比为16.27 dB(图9a、b)，这种情况下解密的数字音频信息质量仍然相当好，能够被人耳清晰辨识。

当7/8的密文信息被剪切时，通过对大量密文信息测量，解密信息的平均信噪比为2.27 dB(图9c、d)，这种情况下解密的数字音频信息仍能被人耳辨别。但是在同等条件下对图像加解密，解密的图像信息只能看到轮廓(图9e、f)。这说明在密文受到剪切攻击情况下，数字音频信息比图像有更好的鲁棒性，

图9 剪切效果及对比Fig.9 Encrypted image pixels are occluded

同时，这种加密也能够有效避免将音频信息直接加密时如果密文部分信息丢失而不能完整解密的缺陷。

3.2.2 密文遭到加入噪声攻击时解密信息的质量

实验结果(图10)显示：

(1)实验时密文中被加入随机噪声，随机噪声的振幅在0-1，在这种情况下解密的数字音频信息的平均信噪比为18.24 dB，信号质量比较好(图10)。

(2)当密文遭到更加严重的噪声攻击时，解密的数字音频信息噪声比较大但是仍然可以被人耳分辨出，而同等条件下解密的图像信息只能看到轮廓。这说明数字音频信息在转化为声图形式后，使用双随机相位编码技术编码和解码有着很好的鲁棒性。

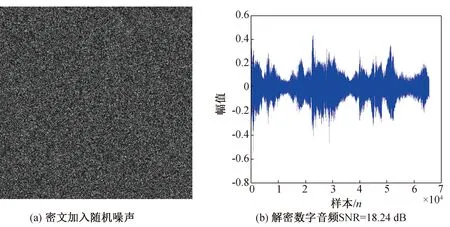
图10 噪声攻击Fig.10 Noise attack

3.2.3 密文通过滤波攻击时解密信息的质量

密文通过高通滤波器，滤波器的大小是256×256像素，中心区域半径是20像素，得出的解密信息的信噪比平均为20.40 dB(图11)。说明在这种情况下解密信息的质量是相当好，也就是说密文可以抵御高通滤波器攻击。

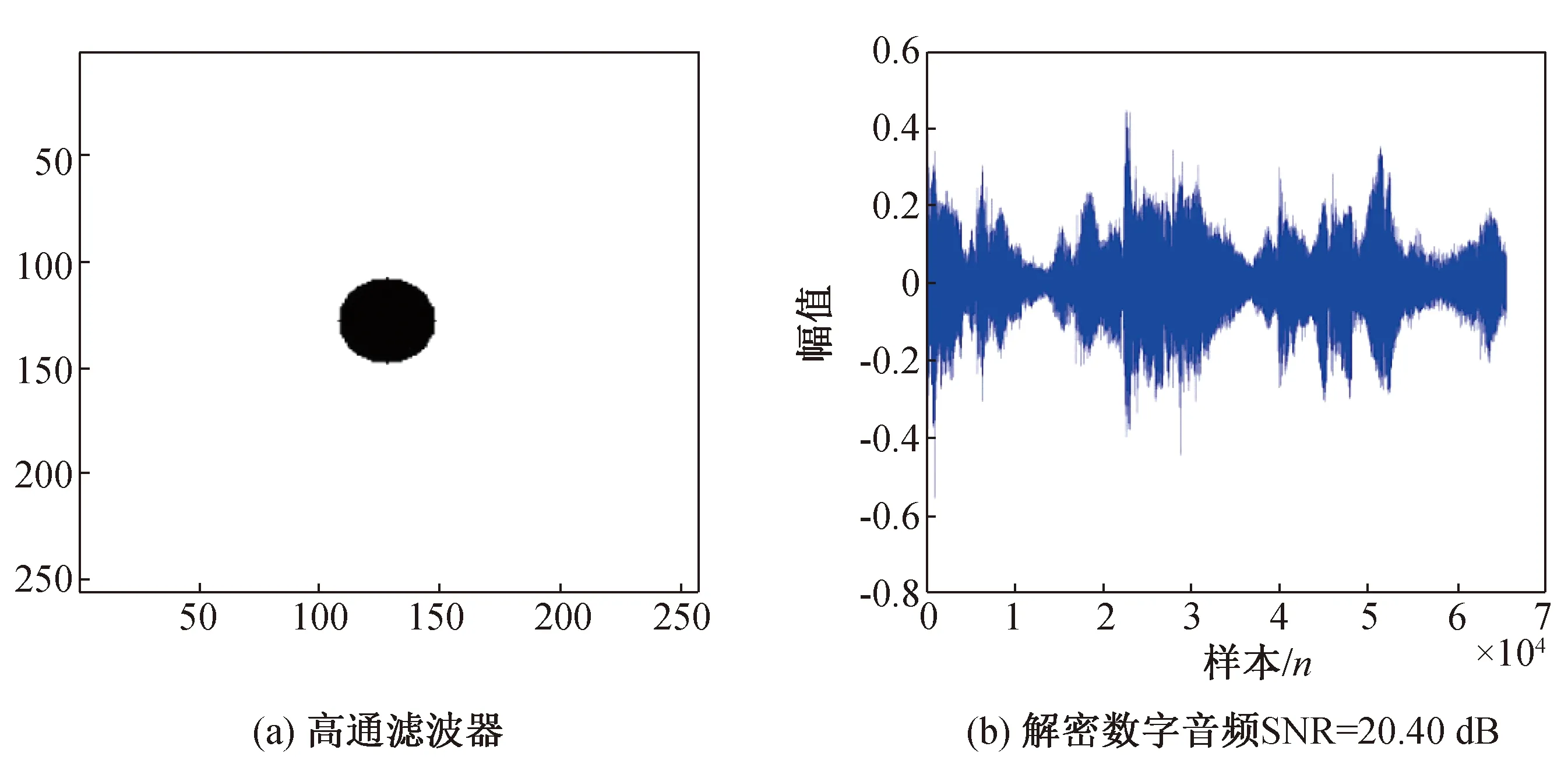
图11 滤波攻击Fig.11 Filter attack

4 结论

(1)本文提出了基于双随机相位编码技术的数字音频信息加密方案，在加密过程中先将数字音频信息转化为二维“声图”形式，再使用猫脸变换对声图进行置乱变换，使原来信息间的统计特性完全被打破，然后使用双随机相位编码技术对声图进行再次加密，密文信息的表现形式是噪声。

(2)加密过程中使用无理数序列构造随机相位板能有效增加密钥空间，提高密钥的可控性，增强信息的安全性。

(3)这种加密思想和方法具有较强的实用性。