基于二维最简颗粒排列的线性与赫兹模型参数研究
2019-07-09张科强陈能远马帅帅
郭 鸿, 曹 龙, 张科强, 陈能远, 马帅帅, 王 普
(1.陕西理工大学 土木工程与建筑学院, 陕西 汉中 723000;2.信息产业部 电子综合勘察研究院, 陕西 西安 710054)
离散元方法(Discrete Element Method,DEM)在当今的科研领域应用愈来愈广泛,如岩土工程[1-2]、地质构造、机械工程等领域。离散元方法着眼于对固体和松散介质力学特性的深入研究,适合描述固体材料中细观、宏观裂纹扩展、破坏累积并断裂、破坏冲击和微震响应等问题。PFC2D/3D(二维/三维颗粒流程序)是离散元方法的主流软件之一,其中线性接触模型和赫兹接触模型是最常用的两个模型。相对于线性接触模型,赫兹接触模型能更真实地模拟球体与墙体、球体与球体的接触效果。刘畅等人[3]通过PFC2D建立了岩石材料的单轴和双轴离散元[4]数值模拟试验,进行了平行黏结有关参数[5-7]标定过程的研究,总结了细观参数与宏观参数之间的关系,方便平行黏结有关参数的确定。徐小敏等人[8]通过室内三轴试验的PFC3D模拟和结果的回归分析,基于线性接触模型建立了颗粒材料初始杨氏模量、初始泊松比等宏观弹性常数与颗粒法向刚度、颗粒刚度比等细观弹性常数间的经验公式。然而,就常用的两种接触模型(赫兹模型和线性模型)而言,其参数之间的相互联系和标定目前尚未见文献报道。
另外,在PFC2D运用过程中[9],首先需要确定颗粒的相关参数,包括颗粒的尺寸,颗粒的刚度、强度,以及剪切模量、泊松比[10-11]等,计算模型参数的正确取值,有利于减少程序调试的次数。
鉴于此,本文以二维情况下规则排列的颗粒为研究对象,以赫兹模量和线性模型为理论基础,在目前国内外学者普遍运用的“试错法”[12]的基础上,深入研究线性接触模型和赫兹接触模型相关参数的关系,推导两种模型关键参数之间的关系。
1 数学模型推导
PFC2D是通过离散单元方法来模拟圆形颗粒介质的运动及其相互作用[13]。赫兹接触和线性接触可承受有限压力,两种模型用不同的计算方法模拟颗粒接触,可模拟材料的本构行为。
线性模型:线性接触模型由常用的剪切刚度Kn和Ks定义相关模型参数(墙体和球体、球体和球体)。
赫兹(Hertz)模型:Hertz-Mindlin 接触是基于Mindlin和德雷谢维奇(1953)理论的近似计算模型,在Cundall(1988)中描述了非线性接触公式。它仅适用于接触球面的情况。赫兹模型的基本参数为剪切模量G和泊松比v。
在PFC2D手册的基础上,对公式进行处理,得出线性模型与赫兹模型在形变量与受力相同的情况下,剪切模量G的计算方法。
线性模型中关于球体的法向刚度:
(1)

切向刚度:
(2)

赫兹模型中球体的法向刚度:
(3)
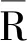
切向刚度:
(4)
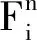
在球体与球体、球体与墙体接触的部分参数计算如下:
球体与球体接触:
球体与墙体接触:
(5)
在赫兹模型中力与形变量的关系为曲线,对形变量积分得出形变量与力的关系式:
(6)

(7)
由式(7)可知:
(8)
由式(5)可知:
(9)
(10)
由式(10)得:
(11)
进一步,可得出:
(12)
由于赫兹模型的参数标定程序相对复杂,而线性模型参数标定容易,因此,在已知最终应力和变形等效的情况下,用线性模型代替赫兹模型进行数值模拟,可以提高计算效率。
2 PFC2D模型建立及数据分析
2.1 规则模型建立

图1 颗粒模型
2.2 线性模型和赫兹模型的数值压缩试验对比
4种规则排列颗粒体系的线性接触模型参数和赫兹模型参数如表1所示,相应的压缩试验结果如图2所示。不失一般性,对于2×1排列颗粒,泊松比取值为0.4,其余排列均为0.1,法向刚度均取为同一数值1.0×107N/m。

表1 颗粒模型参数表

(a) 2×1排列颗粒 (b) 10×1、10×3、10×5排列颗粒图2 线性接触模型和赫兹接触模型接触力与总变形量关系曲线
2.3 相同力与变形量条件下剪切模量与泊松比关系
以10×1颗粒体系为例,分别建立线性接触模型和赫兹接触模型与上节例子相同,线性模型的参数法向刚度取值为1.0×107N/m。以10×1颗粒体系为数值试样进行压缩试验,设定一定压缩量3.79 cm,则线性接触模型的最大接触力为21.1 kN。赫兹模型的参数泊松比取5个值,分别是0.1、0.2、0.3、0.4、0.5,则可以根据两个模型的最终等效确定剪切模量G。赫兹接触模型的数值压缩试验和用式(11)计算所得的剪切模量G和泊松比ν的关系如图3所示。可以看出,模拟值和理论值非常接近,从而验证了式(11)的正确性。
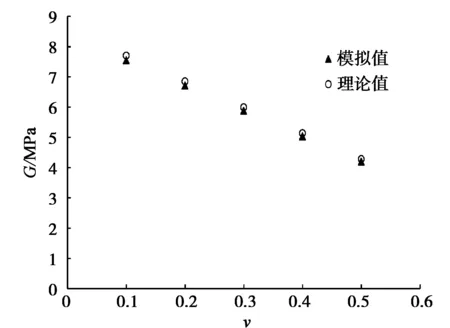
图3 剪切模量与泊松比关系图
3 结 论
本文通过数学推导的方法,提出了离散元数值模拟中线性接触模型和赫兹接触模型参数的相互关系,并通过建立不同排列规则模型的方法,分别用线性接触模型和赫兹模型进行了数值模拟验证。结果表明,所推导的线性模型与赫兹模型的参数正确。
(1)在模型其他参数条件不变的情况下,赫兹模型的剪切模量随着其泊松比的增大而线性减小;
(2)相同条件下,赫兹接触模型的剪切模量随着线性接触模型法向刚度的增大而指数增大;
(3)线性接触模型由于参数标定容易确定,在总应力-应变等效的情况下,可以用本文推导出的公式进行模型代换赫兹接触模型,提高数值模拟效率;
(4)对于不规则排列颗粒模型参数关系的验证及计算方法的改进,还有待于进一步研究。
