多波次导弹发射中的规划问题
2019-07-09孙茜
孙 茜
(上海理工大学 机械工程学院, 上海 200093)
导弹因具有精准打击、打击范围广等优点[1],在现代战争发挥着无可替代的作用。但由于这些特点,导弹部队就可能会成为敌人的首要打击目标。由于每台发射装置只能装载一枚导弹,所以在实施多波次发射时,需要先将上一波次发射任务的车载发射装置机动到装载区域(用于将导弹吊装到发射装置的专门区域)装弹,然后发射装置再机动至下一波次指定的发射点实施发射。因此为了避免敌方对导弹车的打击,需计算导弹出任务的最短时间。
Dijkstra算法是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法,是现有求最短路径的一种比较成熟的算法,其基本思想是设置并逐步扩充一个集合S,存放已求出其最短路径的顶点,则尚未确定最短路径的顶点集合是V-S,其中V为网中所有顶点集合。按最短路径长度递增的顺序,以V-S中的顶点加到S中,直到S中包含全部顶点,而V-S为空。它解决的是有向图中的最短路径问题,该算法的主要特点是以起始点为中心向外层层扩展,直到扩展到终点位置。
本文为了解决在完成紧急任务时车辆导弹部署和机动运输的问题,采用Dijkstra算法为车载导弹的两次连续发射任务提供具体的发射点分配和机动路线方案,使两次发射任务的总体曝光时间最短。
1 导弹位置的布置
问题描述:现有车载发射装置一共24台,依据发射装置的不同大致可以分为A、B、C三类,这三类的数量分别为6、6、12,执行任务之前平均部署在待机地域。该部收到实施两个波次的齐射任务,每波次发射24枚导弹。规划出具体的发射点位分配及机动路线方案,使得完成两个波次发射任务的整体暴露时间最短。暴露时间是指发射装置从待机区域出发时刻至第二波次发射时刻为止的时间,且发射装置位于转载地域内的时间不计入暴露时间内,暂不考虑发射装置在发射点位必要的技术准备时间和发射后发射装置的撤收时间。各地域的具体位置如图1所示,其中D1、D2为待机区域,Z01—Z06为转载地域,F01—F60为发射点位,在本文计算中以D1、D2表示待机区域D1、D2,Z01—Z06表示转载地域Z01—Z06,F01—F60表示发射点位F01—F60。

图1 作战区域道路示意图
约束条件:
(1)各转载地域最多容纳2台发射装置,但不能同时作业,单台转载作业需10 min;
(2)图中主干道路(图中虚线)是双车道,其他道路均是单车道;
(3)A、B、C发射装置在主干道路上的行驶速度分别为70、60、50 km/h,在其他道路上的平均行驶速度分别是45、35、30 km/h。
2 模型的建立和优化
2.1 作战区域道路的距离求解
若要求得最短的暴露时间,就必须算出作战区域示意图中各个相连点之间的距离,若每一小段的两个顶点坐标为(xi,yi)和(xj,yj),则这两个顶点之间的距离为
(1)
2.2 最短路径集的求解
假设待机点Di到各个发射点Fn之间的最短路径集为LDimin,又因为每个待机点的车辆是均分的,所以LDimin中的元素均为12个,设LDimin={d1,i,d2,i,…,d12,i}。
对于最短路径集的问题,本文选择通过Dijkstra算法[2-3]来求得最短路径集,在使用Dijkstra算法计算最短路径时,需要指定起点Di[4],同时需要引入变量Si和Ui分别用来表示已经求出的最短路径的节点和未求出的最短路径的节点[5]。在初始阶段,Si中只包含起点Di;而Ui则是包含除起点之外的所有顶点,从Ui中选出距离最短的顶点Ki,同时将顶点Ki从Ui加入到Si中,更新Ui中各个顶点到起点Di的距离。之所以更新Ui中顶点的距离,是由于上一步中确定了Ki是求出最短路径的顶点,从而可以利用Ki来更新其他顶点的距离,就这样循环反复,直至遍历完所有的顶点,根据遍历完成的所有的点数,可以得到整个路径LDni={d1i,d2i,…,dni}所经过的节点以及其路径的长度lDni={l1i,l2i,…,lni}。
2.3 建立0-1整型规划模型
首先建立0-1整形规划模型[6-7]求解Di待机区域距离最短的24个发射点。设置0-1变量xi(i=1,2,…,15),表示对于待机地域D1是否选择该点为发射点,
(2)
当上一步得到整个路径LD1i之后,从中筛选12条最小路径集LD1min={d1,1,d2,1,…,d12,1},再根据主从干道的权值集Q={a1,i,a2,i,…,a12,i},其中amn∈(0.5,0.8)为主从干道集的元素,根据模型中建立的主次干道速度的大小关系,假设经过一次主干道,则其权值乘以0.8,若经过一次次干道,则其权值乘以0.5,能够得出其带权的最小路径集LD1min·Q,然后对速度集V={v1,v2,v3,v1′,v2′,v3′}进行速度赋权,VQ={q1,q2,…,q24},其中此处的qi∈(0.5,0.8,1),该权值的假设与amn类似,若为A车,则其权值乘以1,B车乘以0.8,C车乘以0.5。当获得第一波单车最长暴露时间,从而可以得知第一波齐射条件下的最短整体暴露时间,时间等于路程除以速度,由此可以得出其目标函数的表达:
(3)
(4)
由于24辆车在部署时平均分配在两个地方,所以分别对选择Di进行判断计算,约束条件:
(5)
综上所述,式(3)、(4)、(5)为0-1整型规划模型。
2.4 模型的求解
根据Dijkstra算法建立最短路径模型,距离D1最近的12个点为:F43、F58、F57、F42、F41、F38、F37、F39、F40、F34、F35、F54,距离D2最近的12个点为F24、F25、F47、F46、F44、F45、F26、F03、F02、F01、F50、F28。根据加权的速度与时间的计算能够得出到D1点的最短时间TD1min=180.9 s,到D2点的最短时间TD2min=143.9 s。由于D2的TD2min值小于D1的TD1min值,所以根据此条件可得,第一波的整体暴露时间为180.9 s,而根据D1的TD1min可以优化D2的TD2min,对D2的TD2min重新进行建模,将第二波的装载时间提前考虑到第一波的模型中来。
2.5 步骤一模型的优化
根据D1的TD1min可知,第二波若要完成与第一波相同的齐射条件,那么D2的TD2min等待的时间会整体增长,那么可以让D1、D2的车一起开,但是D2发出的车可以开到距离转载地域Zi最近的Fi进行第一波齐射,即可增加约束Tmax≤TD1min。D2的目标函数为:
min(lF2i-lZi)=V·VQ·T·xi,
根据上述算法可以判断出新选择出来的D2的路径集中使得min(lF2i-lZi)成立的点为F11、F26、F29、F30、F32、F33、F47、F48、F49、F50、F51、F52,同时将距离D1最近的12个点根据时间约束改为F20、F34、F35、F36、F37、F38、F40、F41、F42、F43、F54、F57。
综上所述:第一波次的机动方案如表1所示,节点分配如图2所示。
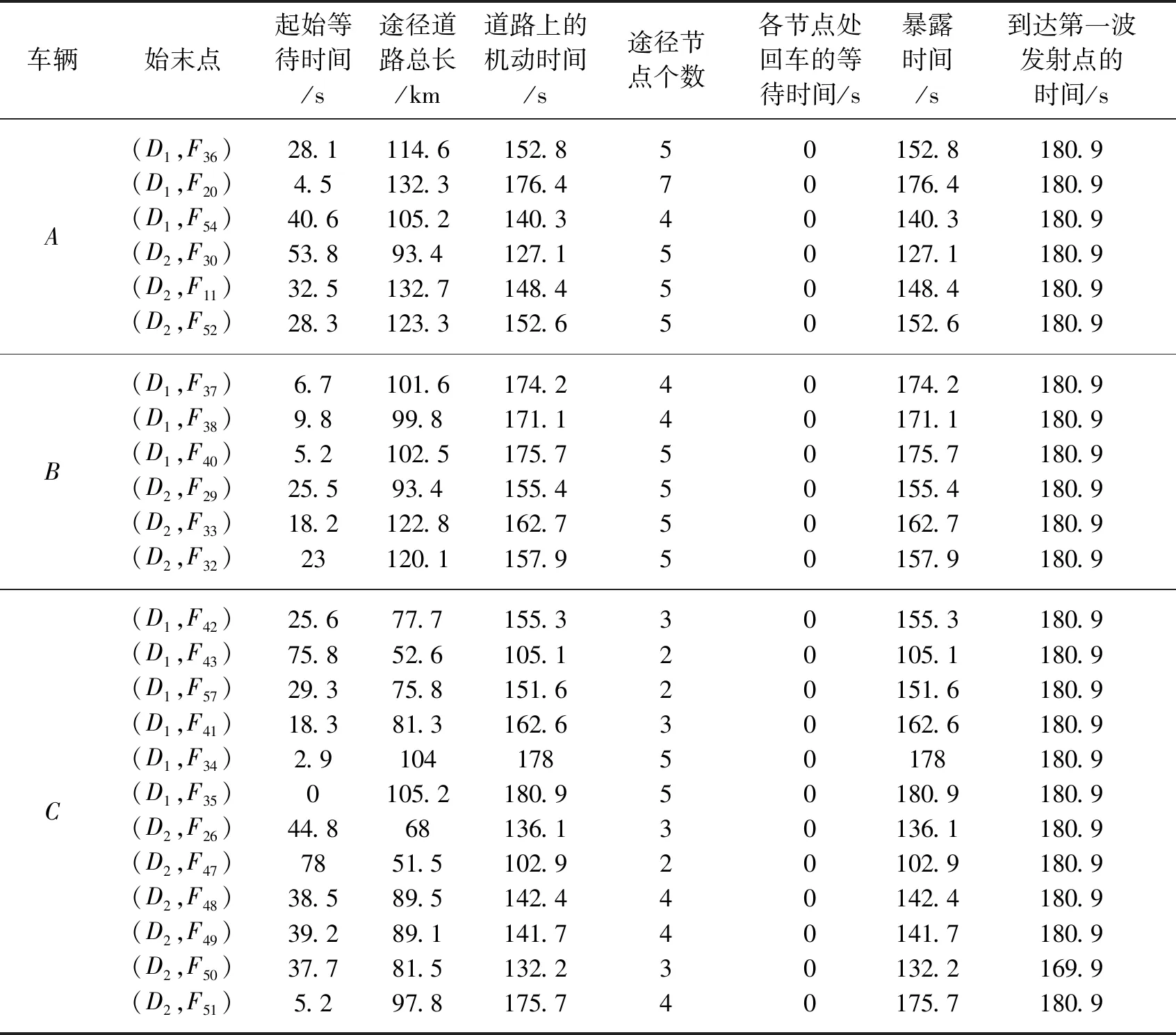
表1 第一波次机动方案分配表
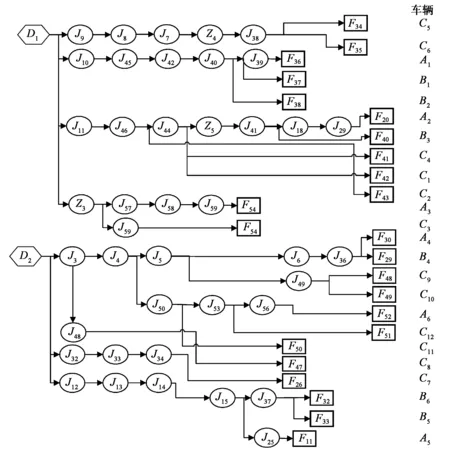
图2 第一波次节点分配图
2.6 步骤二模型的建立
根据步骤一求得各个坐标节点,由于各个节点是确定的,所以需要先通过步骤一的原始模型,再增加约束条件:距离每个Zi周围最近的地方Fi必须被第一波完成,以达到第二波的转载速度最快。其次,在第一波齐射的顶点必须被删除,其数学表达式为
(6)
同时,将上述Fi点确认了之后,通过Dijkstra算法可以得到距离Zi最近的Fi的最短路径集LFimin={f1i,f2i,…,fni},接着分配在此处转载的车辆在最快装载完成之后开往距离LFimin中筛选出来的n个点中的最远的距离,用以获得单车最长暴露时间,从而可以得知第二波齐射条件下的最短整体暴露时间。
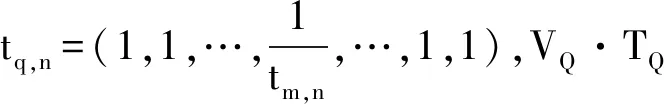
由于此时没有从Di点出发,而是从各个Zi点出发,所以可以抽象为通过从6个Zi点寻找其最短距离。所以0-1整型规划模型的约束条件改为:
(7)
而且每个点寻找的第二波发射点Fi需要根据其距离的加权集合LFimin·Q和速度的加权集合V·(VQ·TQ)进行计算,以获得到达第二波发射点的最短时间,所以,其目标函数为
2.7 问题的求解
根据上述模型的建立以及第一波的求解所得到的各个点,可求得LFimin={f1i,f2i,…,fni},然后根据各个赋权值之后,可以求得发车顺序,从而计算得出使得单车第二波暴露时间最长的路线和各个节点与车型的分配。第二波次的机动方案见表2,节点分配图如图3所示。
综合表1和表2可以得知:两波齐射的最大暴露时间为
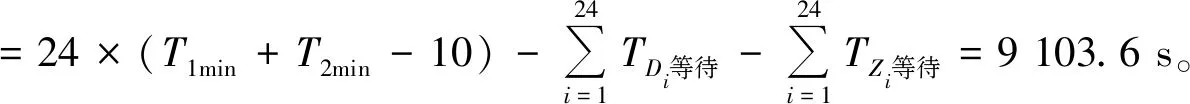
T总 (8)
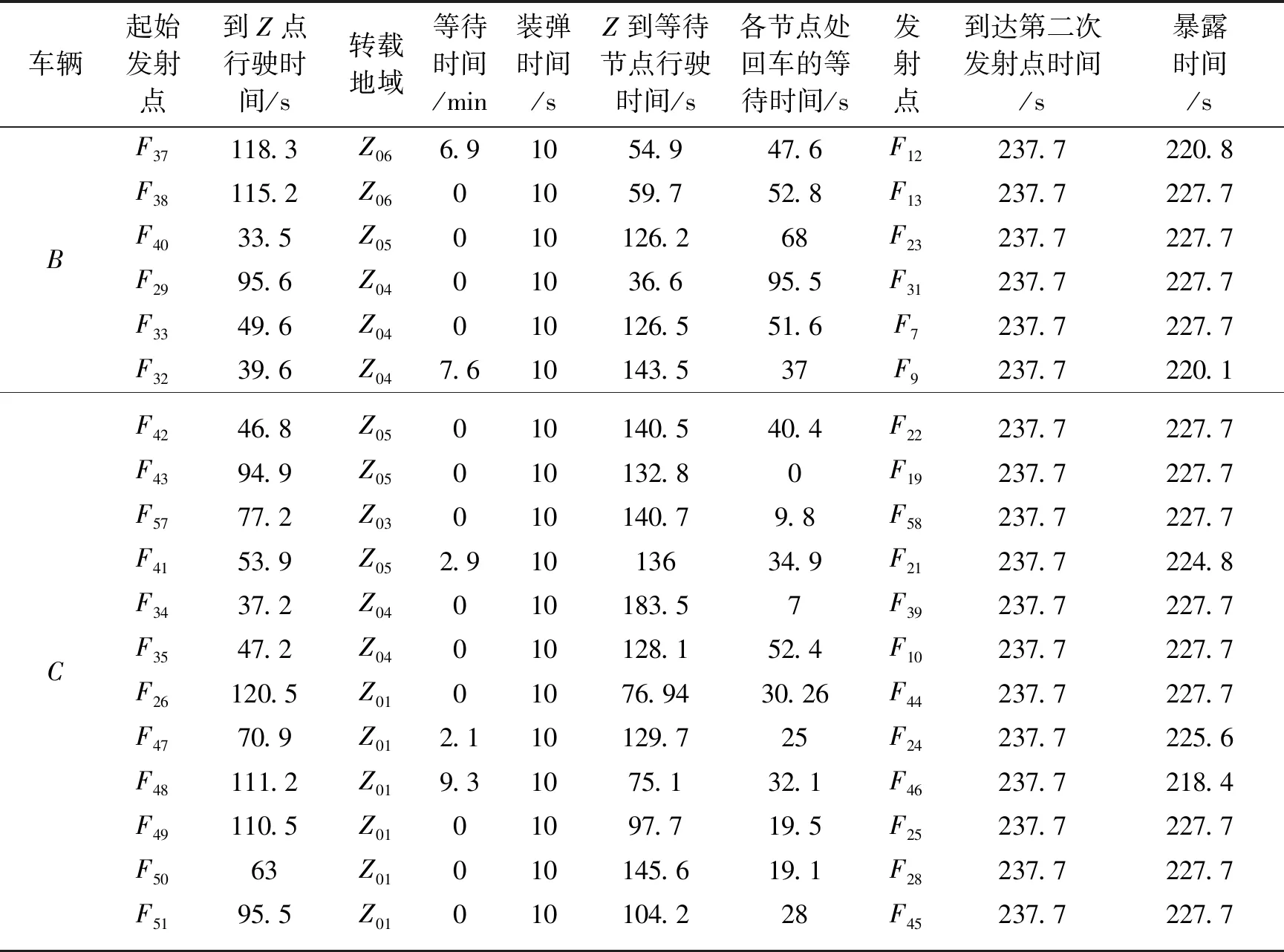
续表

图3 第二波次节点分配图
3 结 论
本文通过对两波齐射问题的分解,将两波齐射问题分解为步骤一和步骤二,步骤一主要解决第一波齐射后所需要的单车最长暴露时间,同时通过模型一选出Di中时间较长的,从而通过时间反馈对模型再一次进行优化,为第二波齐射做准备,并且将第一波在Di处等待时间较长的发射点Fi进行优化。通过步骤一的反馈优化,可以大大提高时间的利用率并且为第二波齐射做充分的准备。
步骤二的模型是建立在第二波齐射关于第一波齐射的一定耦合度上的局部最优解的基础上进行的,第二波齐射任务在考虑了时间权重的基础上求解,可以减少发车顺序错乱而导致的单车暴露时间过长的问题,同时求解LFimin可以得出距离最近的点,从而获得单车暴露最短时间。
文章中所提出的模型是在距离、速度以及真实情况下所建立出来的模型。在此模型下,通过多次反馈、赋权来计算整体暴露时间的最小值,该方法能够有效地解决一些常规的导弹任务分配问题。
