基于小波阈值去噪与EMD分解方法提取润扬大桥振动信息

2019-07-08胡伍生李海锋

振动与冲击 2019年12期

余腾，胡伍生，吴杰，李海锋，乔燕

(1.宿迁学院建筑工程学院，宿迁 223800； 2.东南大学交通学院，南京 210096； 3.同济大学交通运输工程学院，上海 200092)

近年来，伴随交通建设发展的需要，我国建造了大量各种结构的大跨径桥梁[1]。由于各种荷载的叠加作用，桥梁结构会产生振动，一般这些振动从总体安全角度来看是可以承受的[2]。大跨径桥梁一般采用柔性的刚构体系，服役过程中，结构材料本身性能退化造成强度和刚度减弱，同时顾及到一些偶然撞击和极端条件，可能产生影响桥梁安全的变形，结构处于非合理工作状态，甚至造成部分或整体破坏[3-4]。因此，大跨桥梁服役期间必须进行动态变形监测，而获取桥梁结构的振动信息是变形监测的重要目的，也是桥梁动力分析和稳定性分析的基础，当前，以多台GNSS接收机和相关传输、通讯和计算处理设备组成的监测系统在重要或大型桥梁的结构振动监测中已普遍采用[5-6]。由于此种监测方法本质是短基线双差相位观测模型，差分方法不能消除的各种干扰因素的“噪声”仍大量存在，如何从信号中提取有用信息，有效去除“噪声”是我们分析使用这些数据的关键所在。

目前，已有神经网络、算法滤波(卡尔曼、FIR、Vondrak、等)、小波阈值去噪、经验模态分解等方法用于GNSS动态变形监测数据处理中[7-10]。经验模态分解(EMD)方法是一种信号平稳化处理方法，它将信号中不同时间尺度的震荡情况进行自适应地逐级分解，把原始复杂信号分解成线性、稳态的数据序列集，即本征模函数(IMF)[11-12]。但当信噪比低，尤其存在粗差情况下，EMD分解会产生信号畸变；而小波阈值去噪方法可根据噪声和信号的不同幅频特性对信号进行降噪处理，对白噪声有较强的抑制能力[13]。

本文以润扬大桥健康监测系统采集的GNSS连续动态观测数据为例，把改进的小波阈值去噪和EMD分解方法相结合，即首先用改进小波阈值方法去噪，再用EMD方法进一步进行带限滤波，提取大桥振动信号。

1 EMD分解原理及流程

EMD分解是一种自适应信号时频处理方法，较适用于非线性非平稳信号的处理，本质是基于时间尺度把含噪信号从高频到低频逐级分解成各个分量IMF。但须满足两个条件：①由极大值点和极小值点构成的上下包络线平均值为零；②极值点和过零点数量应相等或最多相差一点。

基本分解过程为：首先搜寻信号x(t)的所有极值点，用三次样条曲线连接极大值点形成上包络线；再连接下极值点形成下包络线；不可遗漏极值点。计算上下包络线平均值x0(t)，求差值d0(t)=x(t)-x0(t)。若d0(t)不满足以上IMF的上述两个条件，则将d0(t)再次作为原始信号，再按上述过程计算，得出d1(t)；判断d1(t)是否满足IMF的两个条件，若不满足则重复上述计算直到满足。则dk(t)就是第一个高频IMF分量，即IMF1(t)=dk(t)，计算剩余信号r1(t)=x(t)-IMF1(t)。若r1(t)不是单调函数，则把r1(t)作为新的原始信号x(t)，重复以上计算过程，得到第二个分量IMF2和第二个剩余信号r2(t)。再对r2(t)进行判断，若不满足继续重复上述计算过程，得IMFi和ri(t)。直到ri(t)为单调函数，EMD分解结束。这样就把含噪信号x(t)分解成了从高频到低频的IMF分量和残余分量rn，有

(1)

经总结归纳，其分解流程如下：

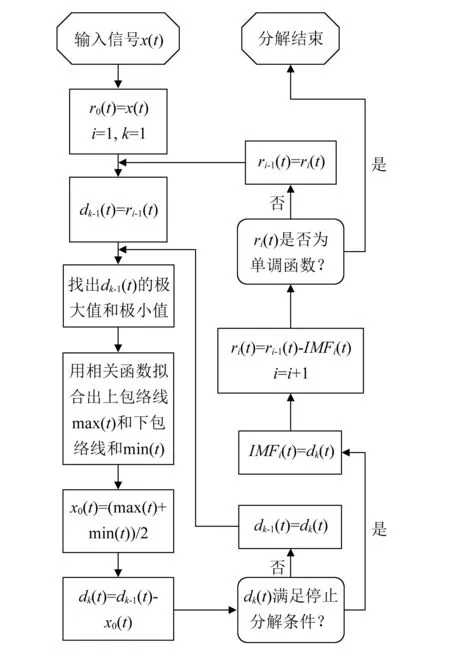
图1 EMD分解流程图

方法把复杂信号分解成有限个瞬时频率有意义的，频率或幅度可受调制的高频、低频分量，具有无需先验知识、自适应性强的优点。

2 小波去噪原理

小波去噪的基本思路是用一族函数去表示或者逼近目标函数。小波母函数ψ(t)必须满足

(2)

式中：ψ(ω)是ψ(t)的Fourier变换，ψ*(ω)是ψ(ω)复共轭函数。

对于能量有限函数f(t)∈L2(R)，小波变换为

(3)

式中：Wf(a,b)为小波变换系数，a为尺度因子，b为平移因子。

小波功率谱

(4)

小波能把信号在不同尺度下进行多分辨率的分解，并把各种频率组成的混合信号分解成不同频段的信号。小波变换使信号能量多数集中到较大信号上，而信号较小的系数包含能量较少。白噪声小波系数的平均功率与尺度成反比，且细节信号幅值随着小波变换级数的增加而减少。白噪声多围绕在幅值较低的小波系数上下震荡，幅值较小且影响力分散的噪声的小波系数必定小于信号的小波系数，据分解式把夹带噪声的函数或信号分解到不同的频率域内，依此设置阈值，使得低于该阈值的小波系数置零，这样可以使得信号中的噪声得以有效控制。

小波分解和重构系数的基本计算过程如下：

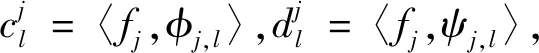
(5)

分解算法

(6)

重构算法

(7)

选择小波基函数和分解层数N，然后按式(7)进行分解；再按噪声先验信息进行滤波，一般来说噪声频率一般较高，能量较低。

经归纳总结，小波分解与重构步骤为：

(1)选择合理的小波基函数和分解层数N，对含噪原始信号进行小波分解，得到各层小波系数。工程数据处理中常用的小波去噪函数有DbN小波、SymN小波，层数一般为3～6层。

(2)确定各层阈值，对小波分解的高频次系数门限阈值进行量化处理。

(3)信号重构，得到去噪后信号。

3 实例分析

3.1 润扬大桥及南汊悬索桥结构振动监测概况

润扬大桥连接江苏省镇江、扬州两市，为中国第一大跨径的组合型桥梁，对华东区域的经济发展、东部沿江沿海交通路网和我国东部国防安全意义特别重大。桥梁全长35.66 km，跨江总长7.21 km，主跨径1 385 m，主塔高度达到300.4 m，大桥主桥部分主要由南汊悬索桥与北汊斜拉桥组成，南汊桥主桥为钢箱梁悬索桥，索塔高209.9 m，跨径布置为470 m+1490 m+470 m；北汊桥为主双塔双索面钢箱梁斜拉桥，跨径布置是175.4 m+406 m+175.4 m，大桥于2005年10月建成通车，是我国建桥史上一座里程碑，其结构振动监测极具重要意义。大桥位于长江下游，桥址地质属长江冲积平原河漫滩地，夏季台风影响明显，季节和昼夜温差较大，恶劣环境影响时有发生。为及时准确掌握桥梁形变信息，在桥梁建成伊始，GNSS连续运行监测系统就得以建设并投入使用。

其中润扬大桥南汊悬索桥的GNSS监测点与基准站布置位置，如图2。

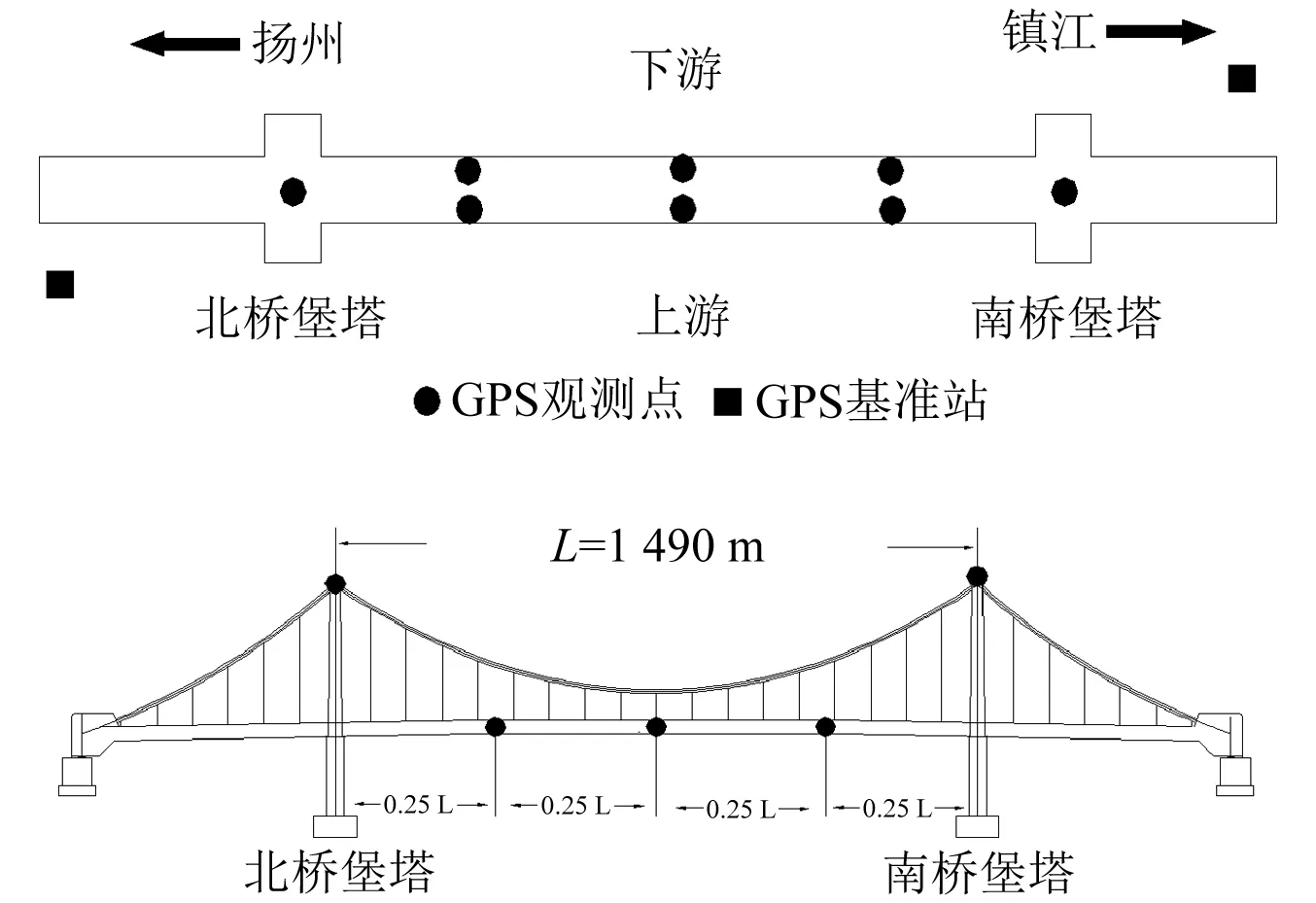
图2 润扬大桥GNSS监测点与基准站布置图

本次试验中采用刚更换的3台Trimble 5800双频GNSS接收机，接收机可同时采集GPS卫星和GLONASS卫星信号，但用于分析解算的数据主要来自GPS卫星信号，其中，一台接收机作为基准站，布设在监控中心的房顶，现场观测环境好，视野开阔，周围无遮挡；另两台作为监测点分别设置在1/2桥跨和1/4桥跨的桥面护栏上，采用RTK差分技术获取振动信号。

本试验数据采集的时间为2015年11月；按动态观测模式进行连续观测，三个测站同步观测约1 h，采样频率为10 Hz，卫星高度角限值设置为15°。

为便于研究桥梁几何位移特征需设定变形监测坐标系统；本项目设定了以桥梁中线的水平投影线方向为X轴，水平垂直于桥梁中线投影线方向为Y轴，竖直方向为H轴的三维空间直角坐标系；GPS接收机采集的数据经过地面站软件解算可以得到监测点在此坐标系下三维坐标变化增量，本文以Y方向的振动位移数据为研究对象，即通常所指的桥梁横向位移。

桥梁结构振动是一种随着时间和空间变化的信息，振动信息包含有用信息和噪声两部分，选取监测数据进行基本分析，为方便研究信号在频域内的特征，做短时傅里叶变换(FFT)，如图3。

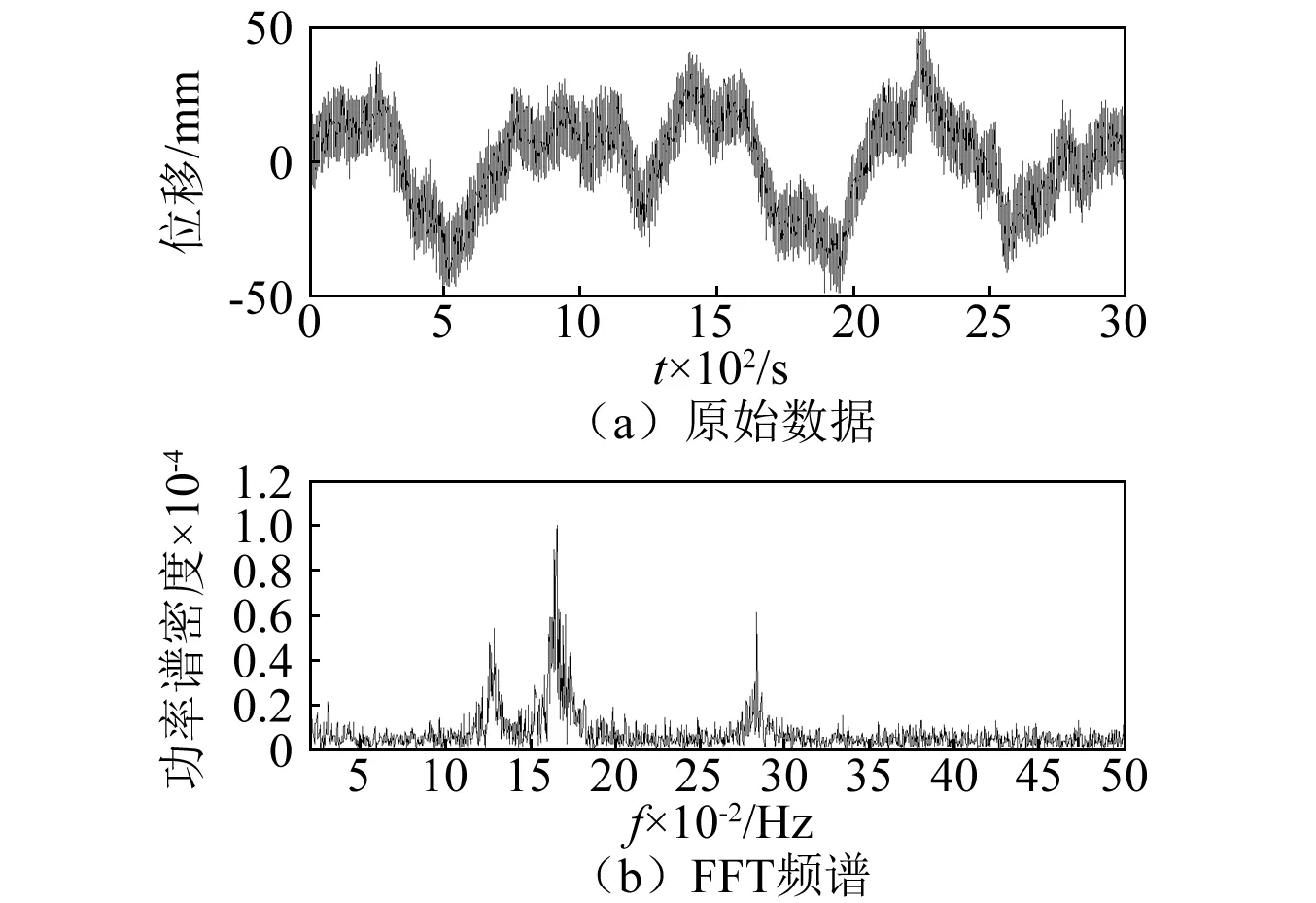
图3 原始数据及FFT变换结果

由图3可见，原始监测信号以零值上下震荡，有一定周期性，功率谱密度偶见峰值，考虑风力和车辆荷载的正常影响量，可认为大桥横向位移没有明显趋势性；作为吊挂钢箱梁的重要受力结构，主缆每根长约2 580.8 m、重达5 022 t，由184束平行钢丝束股构成，由每组相邻监测点的信号分析显示，桥梁结构未见较大整体和局部几何位移，可推断主缆线型和塔柱弯矩正常；数据样本采集当日温度为8℃～15℃，采集时段温度为10℃～12℃左右，温度变化不大，可认为少量温度差异对此影响不明显。其位移主要由风荷载引起，与风速、风向等因素有关[14-15]。由自然随机激励，被激励的主频有三个。

3.2 改进的小波阈值函数

在小波去噪中，阈值如何选取直接关系去噪效果。阈值过小，则处理后的小波系数中仍有过多噪声；阈值过大，则会丢失信号中的部分真实信息，而造成小波系数重构后信号的失真。

常用小波阈值函数为：

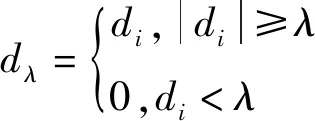
(8)

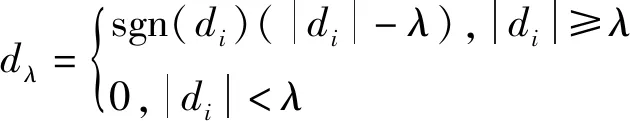
(9)

式中:λ是阈值；di是小波系数的值；dλ是加以阈值处理后小波系数的值。

硬阈值是一种简单的置零方法，把各子空间低于阈值的小波系数直接置零，而大于阈值的系数保持不变；硬阈值函数在λ处和-λ处并不连续，重构后会出现不期望的震荡，失去光滑性。软阈值是把小波系数按固定值向零收缩，该方法整体连续性好，没有附加震荡，但估值与实际值间存在固定偏差，并且软阈值函数的导数不连续，直接影响到重构信号和真实信号的逼近度，因此也有一定局限性。

硬、软阈值法都是对大于阈值部分的小波系数ωj,k进行处理，为了有效弥补以上方法的客观不足，本文对阈值法去噪进行了一定形式的改进，通过选择适当的系数α在软阈值和硬阈值之找到较好的平衡。

基于此，本文给出了改进后的阈值算法，构造了新的函数，为

(10)

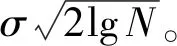
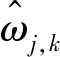
3.3 桥梁振动信号小波基函数的选取

基于在用小波方法过滤大桥振动监测数据噪声时对于小波基选取尚无理论依据的现状，本文也给予一定研究。

小波基函数具有正交性、消失矩、紧支性、正则性和对称性等数学特性，而紧支性、正则性和对称性不能同时满足。消失矩越低，支撑长度也就越短；正则性差，支撑长度就短，计算时间反而省时；增加小波支集长度可让小波光滑；为了保证小波的局部特性又需支集的长度要小，而这样会导致小波不光滑；因此在选取小波基时需综合考虑并有所取舍。离散变形监测数据分析中常用小波基函数特性，如表1所示。

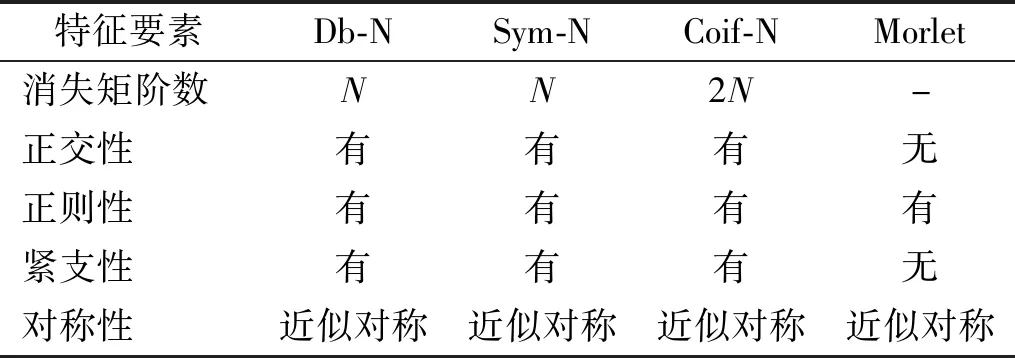
表1 变形监测中常用小波基函数特性列表(参考MATLAB软件中wavelet toolbox)Tab.1 Characteristics of some commonly used wavelet functions for deformation monitoring (reading wavelet toolbox in MATLAB software)

鉴于桥梁振动监测数据量很大，则采用DWT处理效果更好；为避免信号在多尺度分解和重构中边缘部分较大失真，因而采用具有对称性或近似对称性的双正交小波基；为了更好提取信号局部特征，小波基的紧支撑性要好；为避免信号突变，要求小波基有良好正则性和较小消失距。因此，经筛选，选取Db-N系作为研究大桥振动监测数据去噪的实验小波基函数。

实验以某段时间的润扬大桥结构振动连续监测数据为研究对象，数值模拟结合小波基选取的一般原则，选取Db-N小波基系结合实例数据进行研究，实际比较了Db2，Db3，Db4小波基对噪声过滤情况，分析了小波基去噪后残差余量，并基于均方根误差和信噪比指标分析了不同基函数的去噪效果。去噪效果，如图4所示。

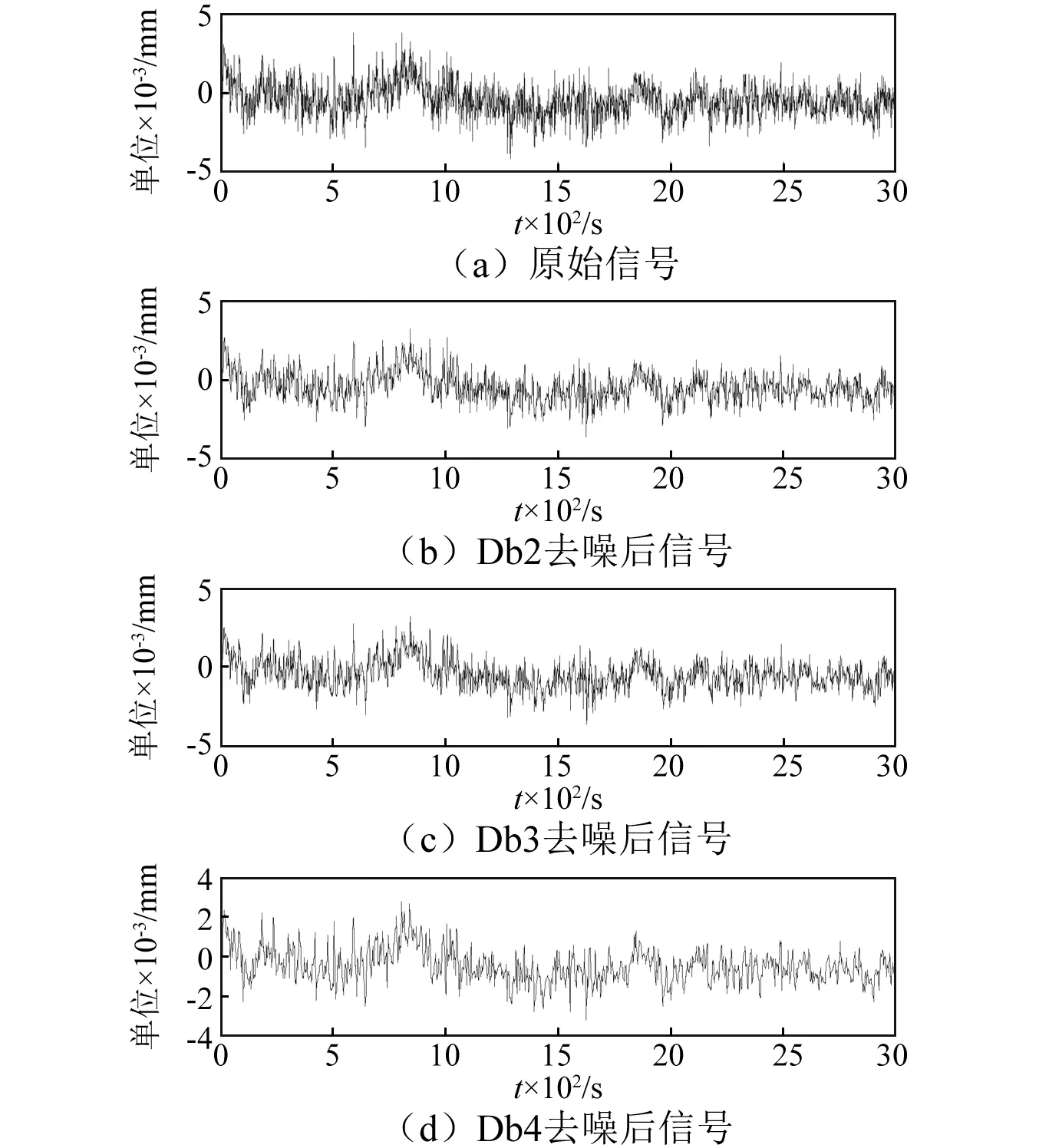
图4 原始信号与各小波基去噪后信号图

由图4可以看出，几种小波基均有一定的去噪作用，Db4小波基去噪后图形更为光滑，效果更优。不同小波基的时频特性差别很大，取信噪比(SNR)指标，SNR值越大表明去噪效果优良，具体值，见表2。

表2 不同小波基去噪效果对比Tab.2 Comparison of different wavelet base de-noising effects

根据桥梁振动信号的特点，经过比较对称性、正则性、正交性、紧支性和消失矩等数学特征，基于所有特征无法同时达到，从桥梁振动信号特性和小波基函数数学属性两方面考虑，顾及主要特征折中选取，本实验采用Db4小波基函数[16]。

3.4 融合方法去噪过程

如上，采用Db4小波基函数进行6层分解，见图5。

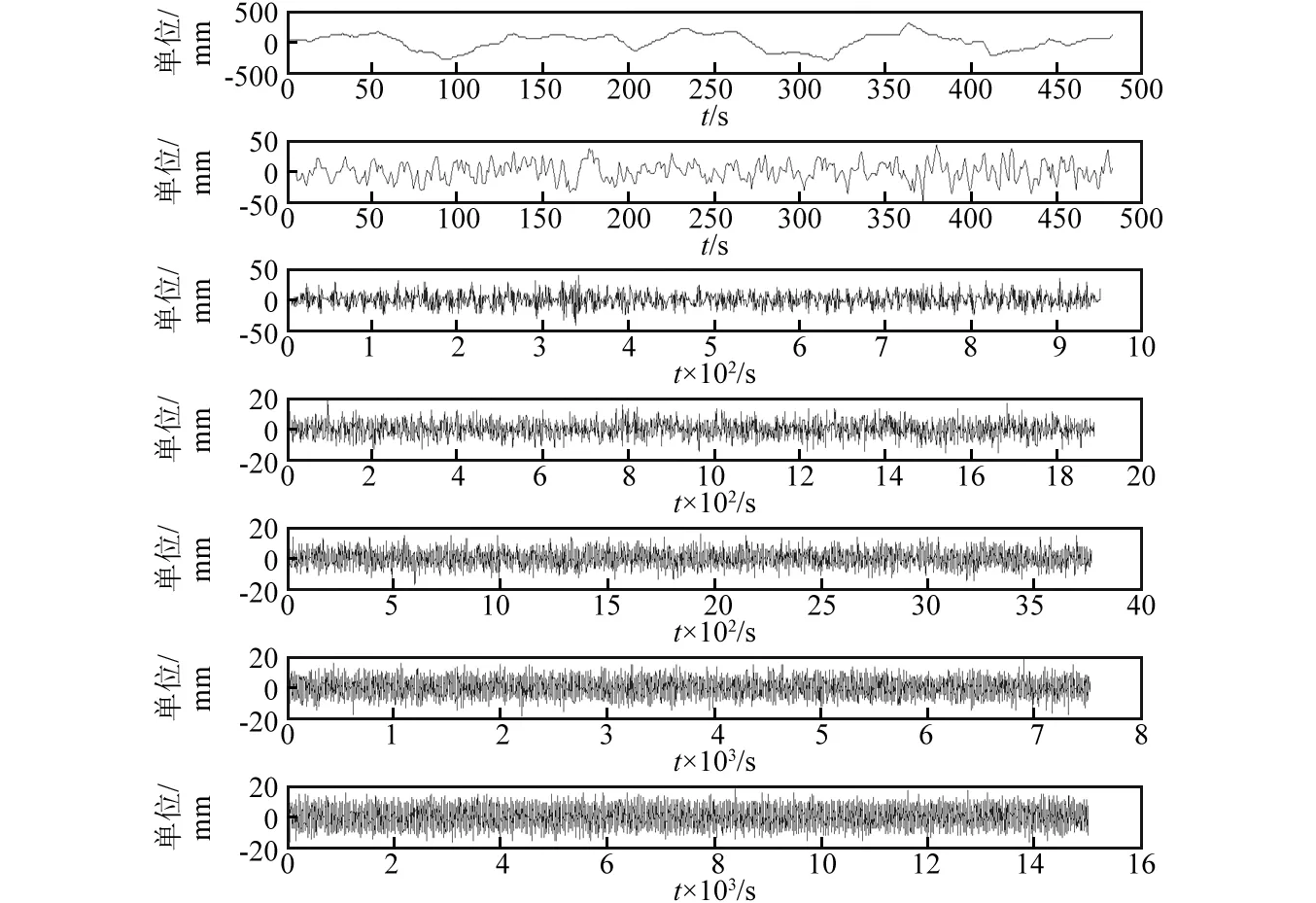
图5 小波分解图(6层)

由图可见，第6层逼近系数基本是趋势部分。选用未经改进的传统的基于无偏似然估计的软阈值法进行滤波，见图6。

用本文改进小波阈值方法进行滤波，选取系数α为0.5，过滤白噪声，过滤后的图像见图7(a)。

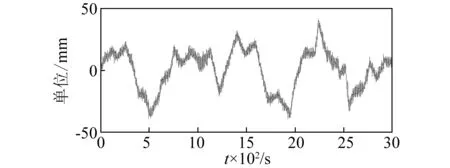
图6 传统软阈值法去噪

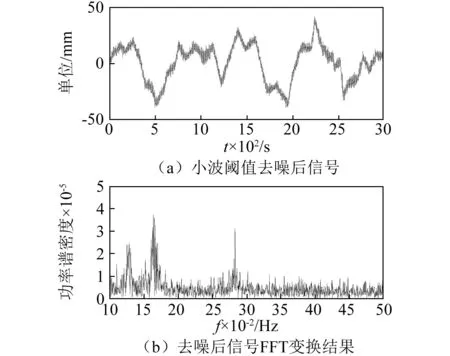
图7 改进的小波阈值去噪及FFT变换

随机选取一桥跨处的监测点的高程数据监测分量做对比研究，选取均方根误差(RMSE)作为评价去噪效果的指标，值越小去噪效果越好，见表3。

表3 传统方法与改进方法数据对比Tab.3 Comparison between traditional methods and improved methods

由图6和图7(a)可见，传统方法与改进方法都能有效地抑制信号中的白噪声，随机选取桥跨北监测点的某监测时段的高程数据进行去噪对比发现，发现改进方法能有约10%的精度提升，见表3。图7(b)为改进小波阈值去噪后的频谱图，由于横向位移振动幅度较小，去噪后功率谱密度整体有所减小，同时也表明了频谱是连续的，占据了整横轴。

经改进阈值法对监测信号进行去除噪声之后，将去噪后的信号做EMD分解，见图8。

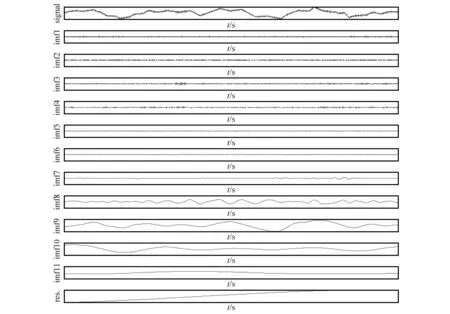
图8 小波去噪后信号EMD分解

由图8可见IMF1～IMF3基本为高频噪声控制分量，因此，进行滤波并对信号进行重构，得到图9。

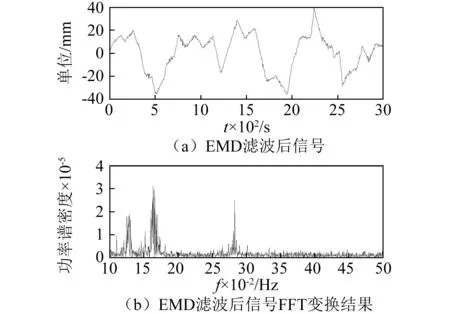
图9 EMD滤波信号及其FFT变换

图9是对小波去噪后的信号用EMD方法进一步频谱滤波。图9(a)是EMD过滤后的信号，相比于图7(a)，显然噪声得到进一步过滤。图9(b)为EMD滤波后信号的频谱图，相比于图7(b)，在图中除主频外其它频段功率得到极大抑制，噪声能量减弱明显，经统计，相对于经过小波阈值去噪后的信号，噪声可进一步减弱60%左右，表明EMD频谱滤波得到很大成功[17]。