一种改进的小波阈值降噪方法
2014-04-27李新君
李新君
(湖南人文科技学院机电工程系,湖南 娄底417000)
0 引言
任何信号在获取和传输的过程中都会受到噪声的干扰,所以,实际应用中获得的信号大都是含有噪声的。若不对含噪信号进行降噪处理则会影响到特征识别、分类等后续工作。信号降噪的目的就是在降低或者去除噪声的同时最大限度地保留原始信号信息。近年来,随着小波分析理论的发展和日趋完善,基于小波变换的信号降噪方法成为了研究热点[1]。
用小波分析方法对信号进行降噪已有很多人进行了研究,也取得了相当多的理论成果。Donoho和Johnstone创立的基于小波变换系数取阈值的方法,取得了很大的成功[2-3]。该方法是为去除一维信号高斯白噪声而开发的。其中小波阈值方法是应用很广且降噪效果相当好的一种小波消噪方法,如硬阈值消噪方法和软阈值消噪法都可取得较好的消噪效果。不过采用硬阈值消噪方法会在某些点产生间断,而这些点有可能包含一些重要信息,采用软阈值消噪方法则可能会造成边缘模糊等失真现象。
针对上述算法的不足,本文提出了一种改进的软阈值去噪算法,主要改进之处是就是当小波系数小于阈值时候,不再是直接地置为零,而是逐渐的减小直到为零;但是当系数大于阈值的时候,就用小波系数幅度值把阈值减掉。仿真结果表明该方法具有较好的消噪效果。
1 小波阈值降噪算法原理
含噪信号经小波分解后,信号的小波系数比较大,噪声的小波系数相对比较小。如何选择合适的阈值以保留信号的小波系数,而让大部分噪声的小波系数置为零是小波阈值降噪的目标。这种方法意味着,阈值化移去了小幅度的噪声或非期望的信号,经小波逆变换后可以得到所需要的信号。由此可见,在小波分析用于降噪的过程中,核心步骤就是在系数上的作用阈值[4]。具体步骤为:①采用小波变换方法对含噪信号进行计算;②对分解得到的小波系数进行非线性阈值分析,阈值处理有硬阈值和软阈值两种方法;③最后再对该信号进行小波逆变换以得到降噪后的原信号。
(1)硬阈值方法

图1 硬阈值函数
硬阈值函数如下:

把含噪信号的小波系数的绝对值与所选定的阈值λ进行比较,那些小于阈值的点变为零,而大于或等于阈值的点则保持不变,这种方法的缺点是在某些点可能会产生间断,而这些间断点却有可能包含重要信息。
(2)软阈值方法
软阈值函数如下:


图2 软阈值函数
就是把含噪信号中的小波系数和阈值λ进行相互比较,把大于或等于λ的点就进行收缩处理为该点值与阈值的差值;小于或等于λ相反数的点收缩为该点值与阈值的和;小波系数绝对值小于阈值的点变为零。软阈值处理相对要平滑,但是可能会造成边缘模糊等失真现象。
(3)阈值的选取
用小波阈值降噪法降噪时,阈值的选择是关键。Donoho于1994年提出了VisuShrink方法,这种方法在最大估计的限制下能够得出最优阈值。阈值一般选取,但是其中的σ是噪声信号的一个标准差,而N则表示信号的长度。即使通过Donoho的理论证明而且还找到了最优通用阈值,但是在实际的应用中效果并不是很理想。
与VisuShrink的方法类似,极小极大(Minimaxi)阈值方法也是一种固定的阈值选择方式。它产生的是一个最小均方误差的极值,而不是无误差。在统计学上,这种极小极大原理用于设计估计器。因为消噪后的信号可以看作与未知回归函数的估计式相似,所以这种极值估计器可以在一个给定的函数集中实现最大均方误差的最小化。Minimaxi阈值计算公式见式3:
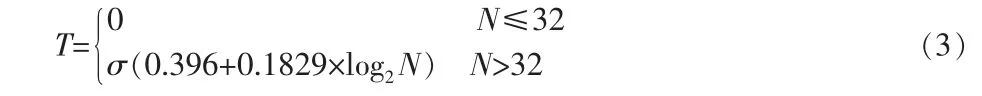
2 改进的小波阈值降噪算法
根据对小波阈值收缩降噪法的分析,可以知道降噪效果不仅与阈值λ的选择有关,还与阈值函数的计算方法有关。目前阈值函数较为成熟的计算方法是软阈值函数和硬阈值函数。但如前所述,软阈值和硬阈值有它们各自的缺点:硬阈值法由于在λ处不连续,所得到的估计信号会产生附加振荡;软阈值法当≥λ 时,与 wj,k总存在恒定的偏差,直接影响着估计信号与真实信号的逼近尺度。
为了能够有效地克服上述方法的缺点,本文提出了一种介于软阈值和硬阈值之间的阈值函数。
阈值函数定义为
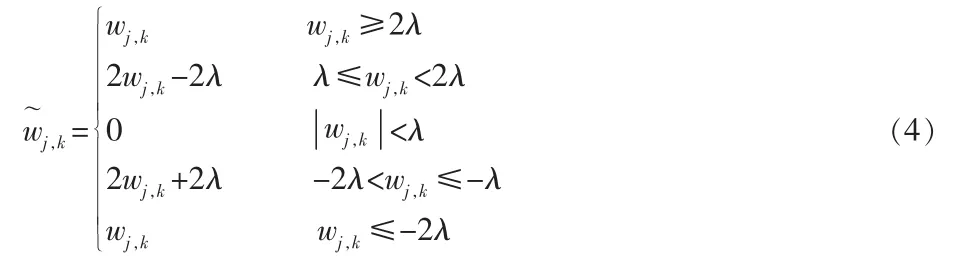
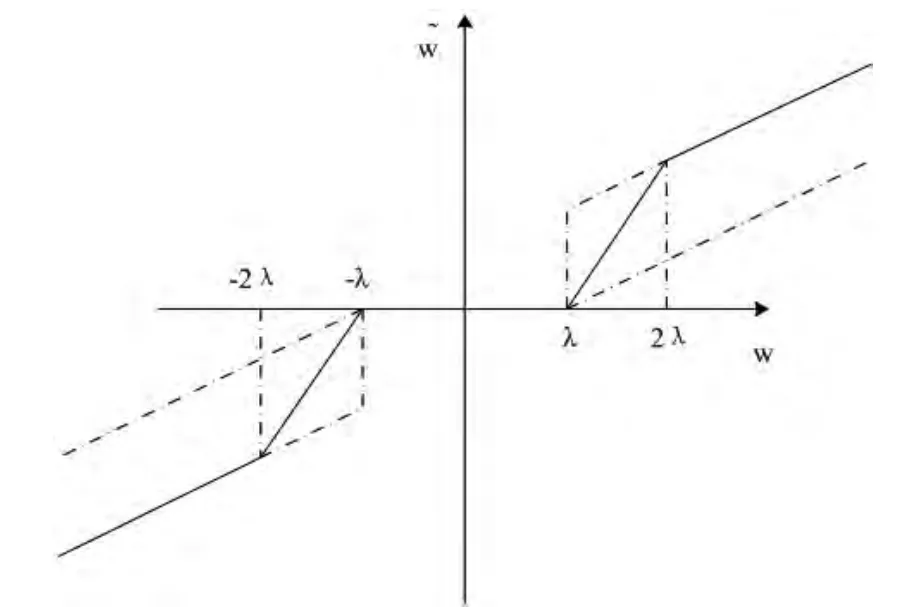
图3 改进的阈值函数
从图3中可知,改进的阈值函数位于硬阈值和软阈值之间。就是当小波系数小于阈值的时候,不是直接地置为零,而是逐渐的减小直到零;但是当系数大于阈值的时候,就用小波系数幅度值把阈值减掉。采用这种做法,既能够保证小波系数的准确性,同时又能保证加阈值后系数的平滑过渡。它就能够有效地避免硬阈值的缺点,同时也改善了在λ处的连续性,最后还能改善估计信号的光滑程度;它有效的克服了软阈值的不足,即当≥2λ 时,与 wj,k不存在的恒定的偏差,提高了估计信号与真实信号的逼近程度。
3 仿真及其结果分析
为了比较硬阈值降噪方法、软阈值降噪方法以及本文所提出的改进算法对降噪的影响,可以利用MATLAB软件进行仿真实验[5]。仿真过程如下:
(1)将lececcum信号加上随机高斯噪声以产生含噪信号;
(2)分解,对含噪信号进行6层分解;
(3)先把第一层的噪声标准偏差求出,再应用Minimaxi阈值方法来计算阈值;
(4)高频系数的阈值选择,对于从第一到第六层的每一层,选择一个阈值,并且对高频系数用本文所提出的阈值处理方法进行处理;
(5)重构,根据第六层的低频系数和从第一层到第六层的经过修改的高频系数,计算信号的小波重构。其仿真得到的结果如图4所示。
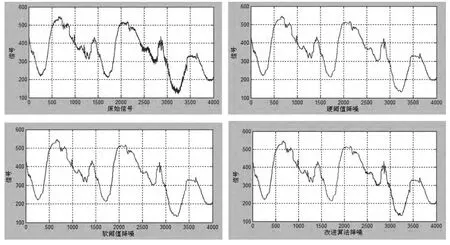
图4 仿真结果
从图4中可以清楚地看到,应用改进的阈值函数进行降噪,确实可以克服硬阈值、软阈值降噪的缺点,能够得到很好的降噪效果。重构的信号既有和原始信号一样的光滑性,又可以很好地保留信号的边缘等局部特征。
4 结束语
本文主要针对小波变换阈值降噪方法中的硬阈值和软阈值函数进行了分析比较。在采用硬阈值方法处理过程中,得到的小波系数在阈值处不连续,有可能引起重构信号的振荡;而由软阈值方法得到的小波系数虽然连续性好,易于处理,可是它与真实的小波系数之间存在着一定的偏差,必然就会降低重构信号的精度。针对以上不足,本文提出了一种改进的小波阈值降噪算法,该方法经仿真验证表明,能够比传统阈值降噪方法更好的去除高斯白噪声,保留原来信号的细节特征,而且算法并不复杂,是比传统阈值降噪方法更为优越的降噪方法,具有一定的现实和推广意义。
[1]翟振兴.基于小波变换的信号去噪研究[D].重庆大学,2010.
[2]刘智.改进的正交小波变换阈值去噪算法研究[J].计算机仿真,2011,8.
[3]S G Mallat.A theory for multiresolution signal decomposition[J].The wavelet representation,IEEE Transactions on pattern analysis and machine intelligence[J].1989,11(7):674-693.
[4]王慧琴.小波分析与应用[M].北京:北京邮电大学出版社,2011.
[5]杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].北京:清华大学出版社,2013.
