基于多尺度排列熵的舰船辐射噪声复杂度特征提取研究
2019-07-08李亚安
陈 哲, 李亚安
(西北工业大学 航海学院,西安 710072)
舰船辐射噪声是被动声呐进行目标检测、跟踪、识别、定位的信号源,研究舰船辐射噪声的特征提取有助于提高被动声呐的工作性能,具有重要的实际工程意义[1-3]。
由于产生机理复杂,且受到复杂水下海洋环境的影响,舰船辐射噪声通常具有非平稳、非高斯、非线性的“三非”特性,使得从中提取稳定特征成为水声领域研究的难点。传统舰船辐射噪声特征提取方法如短时傅里叶变换、功率谱分析[4]、LOFAR谱分析[5]、小波变换[6]等已被实践证明不适用于水声信号处理[7-8]。近年来,经验模态分解(Empirical Mode Decomposition, EMD)[9]与集成经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)[10]的提出为舰船辐射噪声特征提取问题的解决提供了新的思路[7-8,11-13]。刘深等[13]利用EMD分析了舰船辐射噪声各阶固有模态函数(Intrinsic Mode Function, IMF)的能量谱;杨宏等[7]分析了舰船辐射噪声高频IMF与低频IMF之间的能量差;李余兴等[8]利用EEMD分析了舰船辐射噪声最强IMF的中心频率。这些方法取得了一定的分类效果,但样本种类较少,且都只从单一尺度上分析了舰船辐射噪声。
通常来说,信号的非线性越强,其规则性越弱,可预测性越小,复杂程度越高。鉴于舰船辐射噪声具有强非线性,有必要从复杂度的角度对其加以研究。随着非线性动力学的发展,使得表征信号的复杂程度成为可能。至今,已有多种表征时间序列复杂度特征的方法如:关联维数[14]、样本熵[15]、多尺度排列熵[16-17]等。其中,多尺度排列熵所需运算量小、稳定性强、具有多维分析能力,已被广泛应用于故障诊断领域[18-20]。这些应用的成功表明了多尺度排列熵对复杂信号强大的处理能力。
结合水声信号的“三非”特点,针对以上舰船辐射噪声特征提取存在的问题,本文提出一种基于多尺度排列熵的舰船辐射噪声特征提取方法,从复杂度的角度研究水声信号。首先,将实测舰船辐射噪声按尺度分解为一系列子序列,并计算各尺度子序列的排列熵,得到舰船的多维多尺度排列熵特征。进一步,将所提取的舰船多尺度排列熵特征输入概率神经网络(Probability Neural Network, PNN)[21]进行分类验证,实验结果表明了该方法的有效性。
1 多尺度排列熵
排列熵是一种能有效度量信号复杂程度的物理量,信号越复杂,排列熵值越高,反之,则熵值越低。例如,白噪声的排列熵值最大而正弦信号的排列熵值最小。
多尺度排列熵是排列熵的改进,其思想是先将时间序列进行多尺度分解,再计算各尺度子序列的排列熵,进而从多个维度描述信号的复杂度。给定一维时间序列{x(i),i=1,2,…,N},将其按式(1)进行多尺度分解:
(1)
式中:s为尺度因子,1≤j≤N/s,ys为尺度s下的子序列。对尺度s下的子序列,按如下步骤计算其排列熵:
1)适当选取嵌入维数m与时间延迟τ,按式(2)重构其相空间:
(2)
式中:Ys为重构矩阵,K=N/s-(m-1)τ。
ys(t+(j1-1)τ)≤ys(t+(j2-1)τ)…≤ys(t+(jm-1)τ)
(3)
令πt={j1,j2…jm}表示该行各元素的原始位置,则πt表征了该行的排列方式。显然,Ys中的任一行均有m!种可能的排列类型,对每一行重复上述步骤,统计得到每种排列类型出现的频数hl与概率pl=hl/K。
3)根据式(4)计算得到尺度s下子序列的排列熵:
(4)
进一步,对其他尺度下的子序列按上述步骤计算其排列熵,便可得到原始时间序列的多尺度排列熵。在计算多尺度排列熵时,原始时间序列的长度N,尺度因子s,嵌入维数m和时间延迟τ的选取至关重要。根据前人的研究结果[22-23]与大量实验研究,本文取N=8 820,s=1~10,m=3,τ=1。
2 特征提取
本文对五类实测舰船辐射噪声进行特征提取实验。舰船辐射噪声数据采集自中国南海,实验位置水深约4 000 m,海底近似平底,数据采集在一级海况条件下进行,风浪噪声较小。全向水听器由实验船布放至水下30 m处,水听器灵敏度为-170 dB re 1v/μpa,频率响应为0.1 Hz~80 kHz,水听器另一端与采样频率为44.1 kHz的数字采集仪相连。为减小自噪声对信号采集的影响,实验船发动机在数据采集过程中熄火。水听器布放完成后,五类舰船先后以8节航速在实验船1 km外航行。本文特征提取实验中,每类舰船各有148个样本,每个样本包含8 820个数据点(0.2 s)。为了分析、比较多种特征提取算法的优劣,本文分别利用基于EEMD的最强IMF中心频率法、高低频能量差法与基于复杂度的排列熵和多尺度排列熵分析以上数据。
2.1 基于EEMD的特征提取
利用EEMD对五类舰船辐射噪声进行模态分解,结果如图1所示。可以看出,EEMD将各类舰船辐射噪声分解为一系列从高频到低频排列的IMF。由于EEMD是一种自适应的模态分解方法,因此,不同类别舰船辐射噪声分解后得到的IMF阶数不同,图1仅列出有代表性的前六阶IMF。对这些能反映信号不同振动状态的IMF进行信息挖掘,便可得到不同类别舰船辐射噪声的振动特征。

图1 五类舰船辐射噪声的EEMD分解
采取与文献[8]相同的IMF中心频率、平均强度定义,对五类舰船辐射噪声进行分析,图2和表1分别给出了五类舰船各148个样本最强IMF中心频率的分布情况和统计特性。可以看出,除第二类舰船有少量离群值外,第一、二、三、五类舰船的最强IMF中心频率分布范围相对固定,最强IMF中心频率的均值相差较大,可分性强。但是,第四类舰船的最强IMF中心频率与第三类舰船重叠严重,难以区分,且其分布不均匀,过多的离群值还可能对第一、二类舰船的识别造成影响。
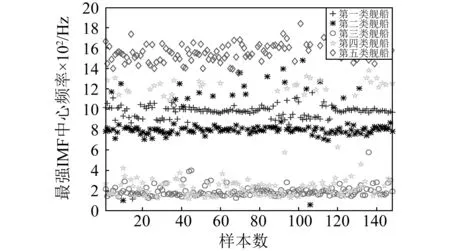
图2 五类舰船辐射噪声的最强IMF中心频率

中心频率第一类第二类第三类第四类第五类均值/Hz974.71842.31195.49466.191922.11标准差/Hz88.32177.3455.22434.62110.49
进一步,采取与文献[7]相同的高频(1 kHz~10 kHz)、低频(0~1 kHz)以及能量定义,分析五类舰船辐射噪声经EEMD分解后各阶IMF的高低频能量差,结果如图3、表2所示。可以发现,第二、三、四、五类舰船的高低频能量差分布均匀,尽管第二、四类舰船的高低频能量差均值接近,利用这一特征依然能较好区分两类目标。但是,第一类舰船的高低频能量差分布不均,且与第二、三、五类舰船的高低频能量差特征存在重叠,不利于区分几类目标。
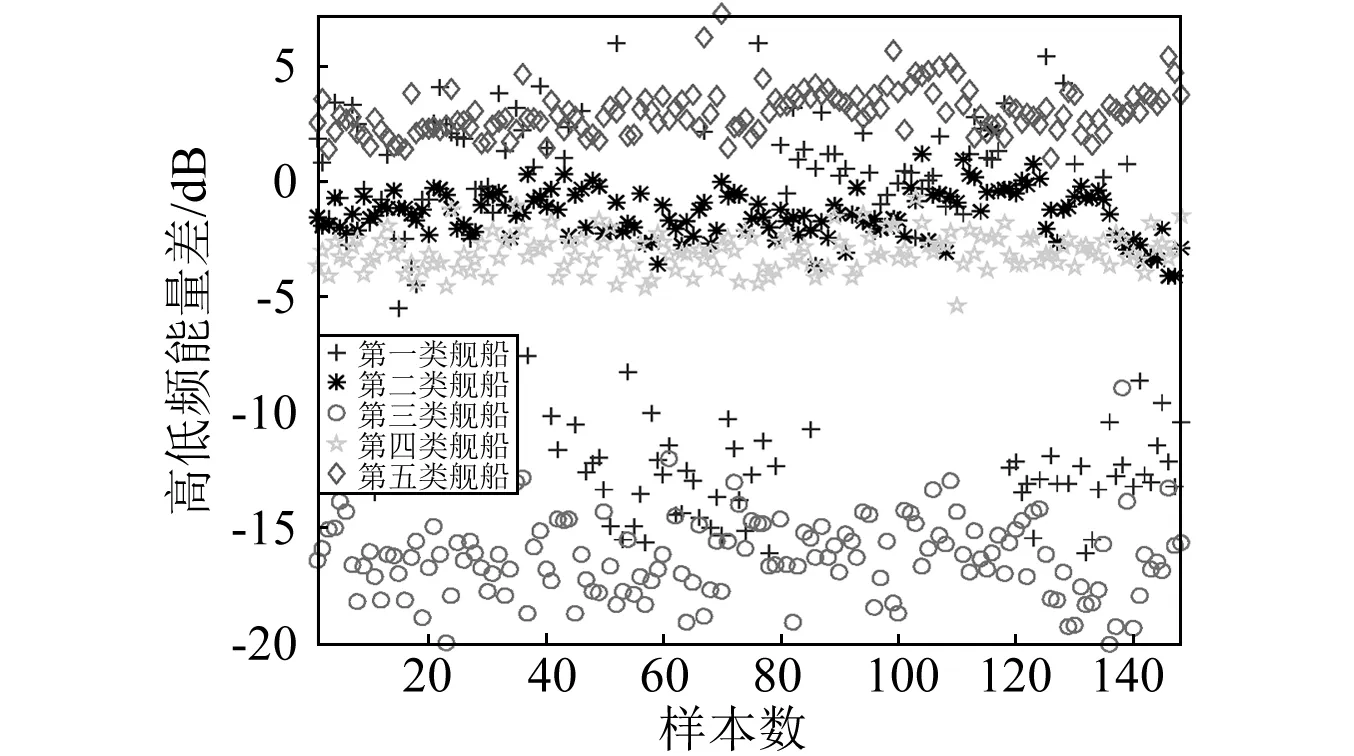
图3 五类舰船辐射噪声的高低频能量差

高低频能量差第一类第二类第三类第四类第五类均值/dB-4.83-1.38-16.29-3.053.03标准差/dB6.9421.061.710.790.99
2.2 基于复杂度的特征提取
传统的舰船辐射噪声特征提取方法分析了信号的频率、能量特征,本文则从复杂度的角度出发。首先提取五类舰船辐射噪声的排列熵特征。由图4和表3可知,五类舰船的排列熵特征分布均匀,表明了排列熵算法具有较强的稳定性和一致性。由于五类舰船辐射噪声的产生机理不同,其复杂程度理应存在差异,而排列熵很好地度量了这种差异。由平均排列熵值大小可见,第三类舰船的排列熵值最高,信号最复杂,随后是第一、第五、第二和第四类。从排列熵特征分布来看,除第一与第五类舰船的排列熵特征分布略有重叠外,排列熵特征可以很好的区分五类舰船辐射噪声。
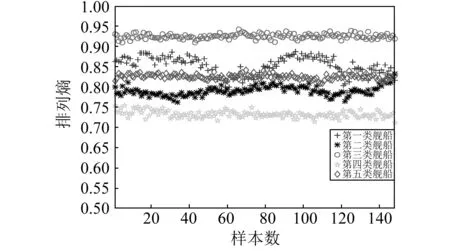
图4 五类舰船辐射噪声的排列熵

排列熵第一类第二类第三类第四类第五类均值0.8520.7910.9250.7320.825标准差0.0230.0120.0060.0080.006
为了进一步提升排列熵特征的可区分性,引入多尺度排列熵从多个维度分析五类舰船辐射噪声。五类舰船148个样本在各尺度上的排列熵均值和标准差分别由图5、表4和表5给出。从图5和表5可以看出,五类舰船辐射噪声在各个尺度上的排列熵分布均匀,离群值少,再次突显了排列熵算法具有较强的稳定性和一致性。此外,从图5和表4还可以看出,尽管在某些尺度上,某几类舰船的复杂程度相似,排列熵均值接近,但得益于多尺度排列熵的多维分析能力,每一类舰船都能在一些尺度上得到明显区别于其他类舰船的熵特征,大大提升了舰船的可识别性。
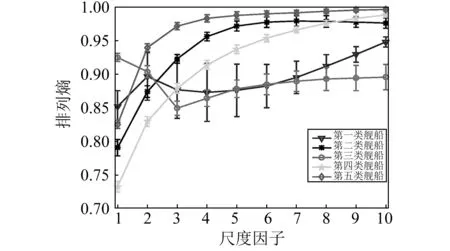
图5 五类舰船辐射噪声的多尺度排列熵
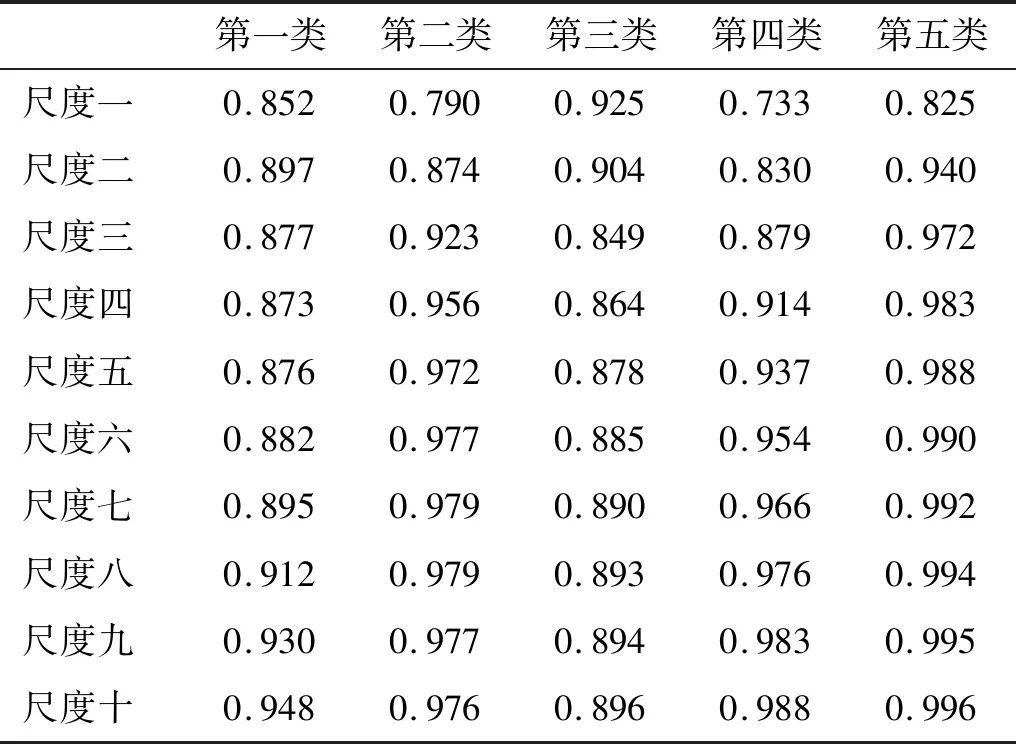
表4 五类舰船辐射噪声的多尺度排列熵均值Tab.4 The average multi-scale permutation entropy of five types of ship radiated noise
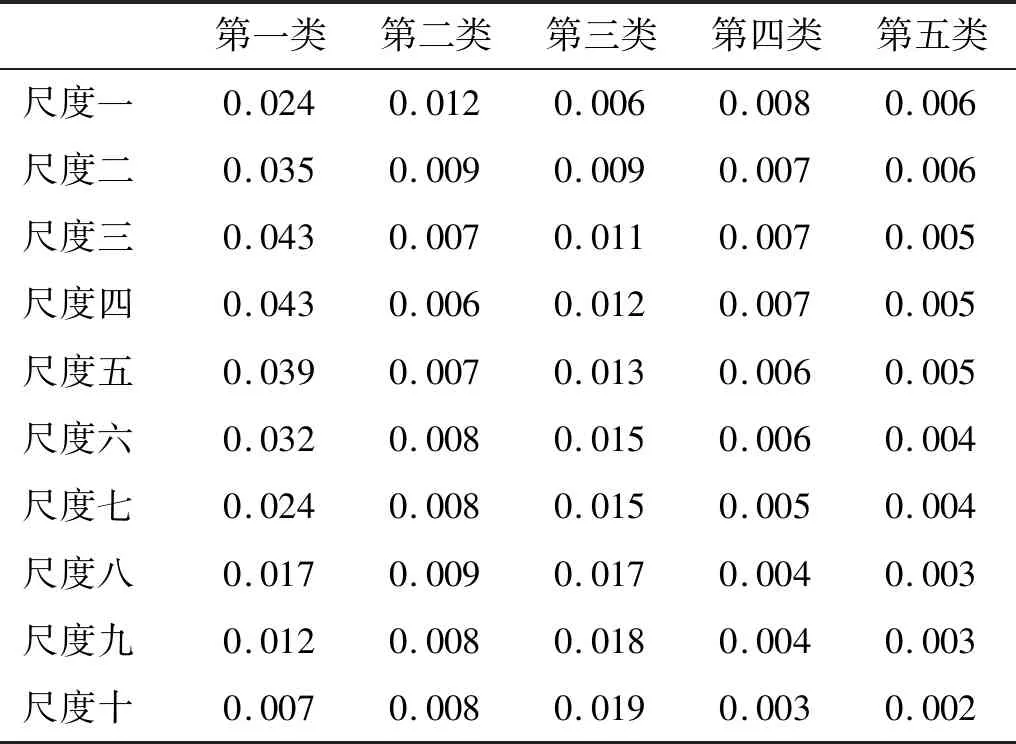
表5 五类舰船辐射噪声的多尺度排列熵标准差Tab.5 The standard deviation of multi-scale permutation entropy for five types of ship radiated noise
3 模式识别
为了进一步比较几种舰船辐射噪声特征提取方法,引入概率神经网络[21]进行分类验证。对每种特征提取算法,随机选取每类舰船48个样本作为训练样本进行分类器训练,随后利用每类舰船剩余的100个样本作为测试样本得到分类结果,详细分类结果由表6~表9给出。
表6的分类结果与图2的特征提取结果基本吻合,基于最强IMF中心频率的特征提取对第一、三、五类舰船的识别率超过99%;而第二类舰船与第一类舰船的中心频率特征接近,部分样本被识别为第一类舰船,因此识别率稍低;特别地,由于第四类舰船的最强IMF中心频率分布不均且与其他类别舰船特征存在重叠,神经网络分类器无法对其进行识别,识别率为0。类似的,表7的分类结果与图3的特征提取结果相吻合,由于第一类舰船的高低频能量差特征分布不均,分类器无法对其识别,识别率为0;第二与第四类舰船的高低频能量差特征相近,因此识别率分别为69%和84%;第三与第五类舰船的高低频能量差特征可区分性强,识别率高于99%。总体来说,基于EEMD的特征提取方法识别率高于70%,与文献[8]的研究结果相同,最强IMF中心频率特征要优于高低频能量差特征。
表8的分类结果与图4的排列熵特征提取结果吻合,基于排列熵的舰船辐射噪声特征提取方法对第三、四、五类舰船的识别率达到100%;由于第一、二、五类舰船的排列熵特征略有重叠,因此分别有50个和17个第一类和第二类舰船被识别为第五类。尽管如此,排列熵的总体识别率依然高达85.2%,优于基于EEMD的特征提取方法。表9为基于多尺度排列熵的分类结果,由于可以从多个维度描述信号,因此,多尺度排列熵对每类舰船都有较好的识别率,总体识别率高达95.8%,显著高于只能从单个尺度描述信号的基于EEMD的特征提取方法和基于单尺度排列熵的特征提取方法。
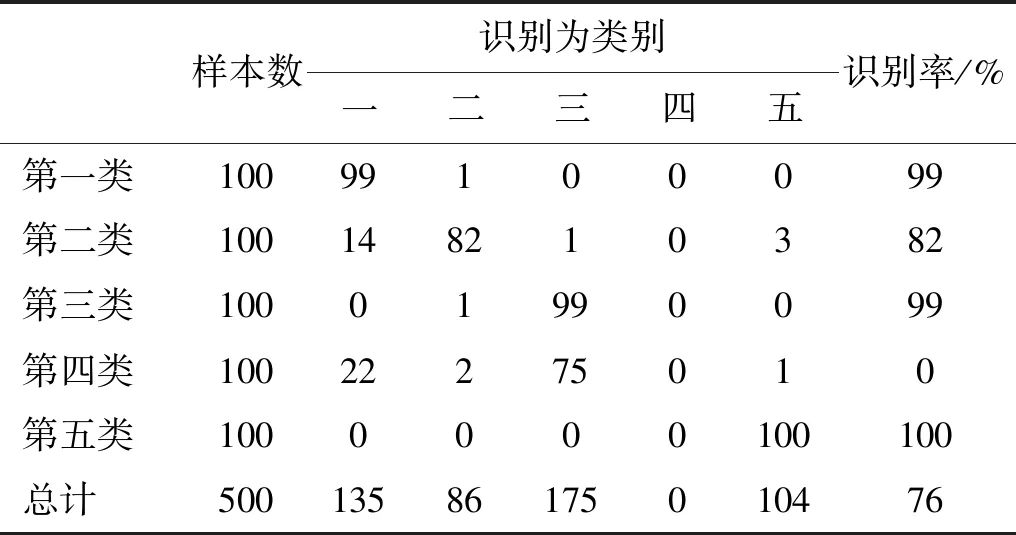
表6 基于最强IMF中心频率的概率神经网络分类结果Tab.6 The PNN identification results based on the center frequency of IMF with the highest energy
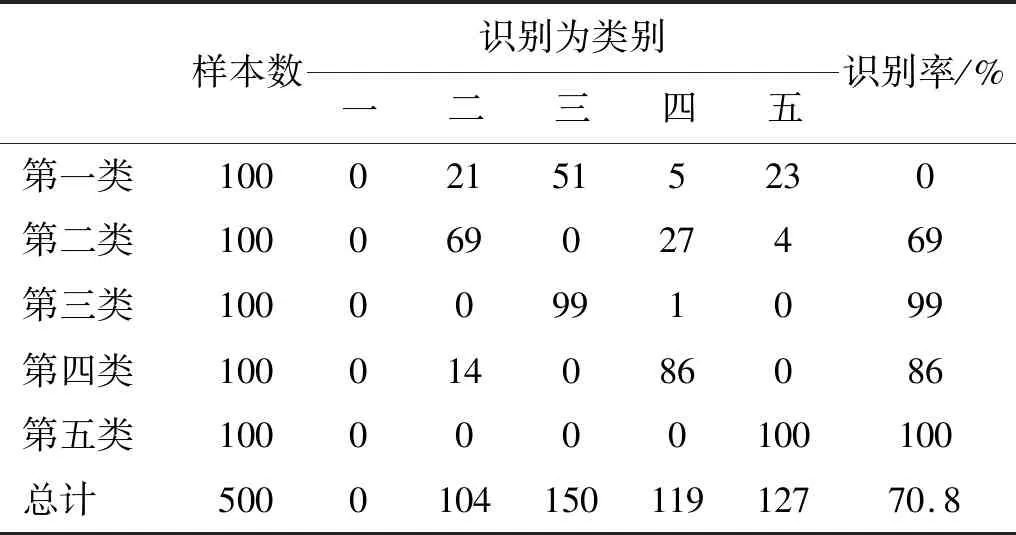
表7 基于高低频能量差的概率神经网络分类结果Tab.7 The PNN identification results based on the energy difference between high and low frequency
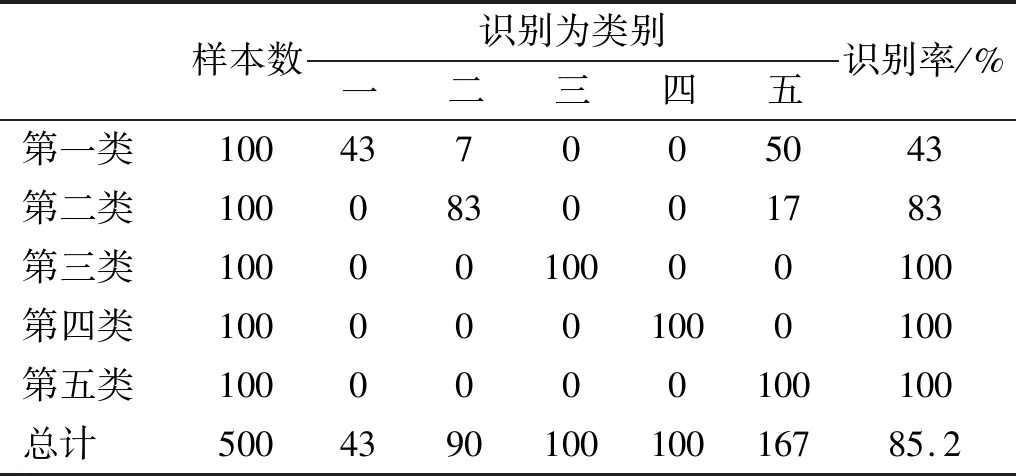
表8 基于排列熵的概率神经网络分类结果Tab.8 The PNN identification results based on permutation entropy
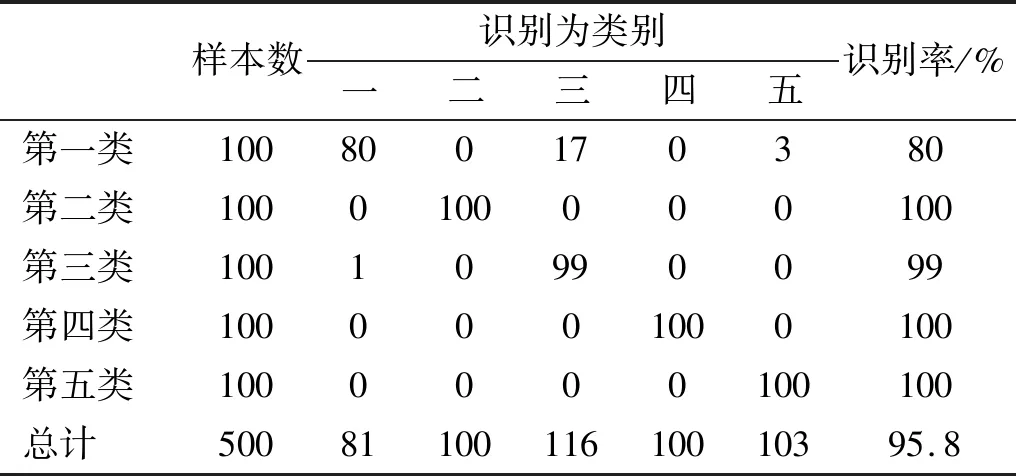
表9 基于多尺度排列熵的概率神经网络分类结果Tab.9 The PNN identification results based on multi-scale permutation entropy
4 结 论
本文提出一种基于多尺度排列熵的舰船辐射噪声特征提取方法,从复杂度的角度研究舰船辐射噪声,通过实测舰船辐射噪声特征提取和分类识别实验表明:
(1)不同类别舰船辐射噪声的产生机理不同,其复杂程度存在差异,复杂度特征是一种有效的舰船识别特征。
(2)多尺度排列熵只需要较短数据(0.2 s)就能获得稳定的熵值,是一种稳定性强、一致性好的复杂度特征提取方法。
(3)多尺度排列熵可以从多个维度描述舰船辐射噪声,具有很强的可分性。以多尺度排列熵为特征的分类识别效果显著优于只能从单个尺度描述信号的基于EEMD的特征提取方法和基于单尺度排列熵的特征提取方法。
