面向车-人碰撞事故的人-地摩擦因数可靠性分析

张晓云， 杨小波， 张东明， 侯心一

(1. 上海交通大学 机械与动力工程学院，上海 200240； 2. 上海市公安局交通警察总队，上海 200070)

交通事故再现作为一门数字化仿真技术，可为事故认定提供有力依据。事故再现类型中又以车-人接触碰撞事故较为常见和复杂。此类事故包含了人-车-地三个系统及其相互作用，涉及变量多，因此，车-人交通事故数值再现一直是交通安全研究中的焦点问题[1]。鉴于实际道路环境的复杂性，数值计算中往往存在诸多不确定因素。充分考虑不确定因素并采用不确定性方法分析其对道路交通事故再现结果的影响，对于提高再现分析结果的可靠性和准确性[2-3]具有重要意义。其中，行人摩擦生物力学特性对车人碰撞事故再现结果有直接的影响[4]。事故数值再现计算中，在落地瞬间运动状态相同的前提下，人-地接触摩擦因数直接决定了行人最终落点位置和姿态，进而对车辆初始速度推算产生影响，是事故再现计算中关键参数之一[5]。已有的部分研究中，人-地摩擦因数常作为定值或均匀分布处理[6-7]，未考虑到该参数的不确定性对计算结果的影响。

车-人接触碰撞事故中，行人落地姿态是计算精度和准确性的重要评判依据，车辆初始速度则是事故认定的关键参数。本文将基于交通事故典型案例，选取行人-小客车低速碰撞且行人落地后在地面运动状态以滑移为主的案例为分析对象，对车-人接触碰撞事故中的人-地摩擦因数特性进行深入探讨与分析，考察在碰撞形态、行人高矮、汽车外廓形状、碰撞速度等因素一定的前提下，行人在与地面接触后由于不同的人-地摩擦因数所导致的运动状态差异，由此建立行人落地姿态和车辆初速度与人-地接触摩擦因数之间的可靠性分析模型，进而对人-地摩擦因数的不确定性进行分析，考察其对于行人落地姿态和车速推算的影响；在此基础上给出该参数测量精度要求以及相应不确定程度下车辆初速度的置信区间。

1 三维接触模型构建

在某典型车-人碰撞事故案例中，通过现场勘查发现，行人分别和事故车辆的保险杠、发动机罩、挡风玻璃发生接触，之后在空中翻转后落地，滑行一段距离后停止在人行横道线上。行人落地后的位置与姿态通过现场勘查记录和法医检验报告获得。

根据现场勘测结果，绘制如图1所示的事故现场示意图。事故现场有一辆小客车，该车右前轮、右后轮分别距公路北侧机动车道边缘线2.30 m、2.18 m，右前轮制动拖印长12.58 m，始点距边缘线2.02 m。行人垂直于道路走向倒卧于小客车前方，头部中心和脚跟分别距边缘线2.46 m、3.83 m，头部距小客车右前轮3.61 m，现场测得行人地面滑移痕迹为4.19 m。右前轮测量的基准点为其西北方14.23 m的路口信号灯杆。

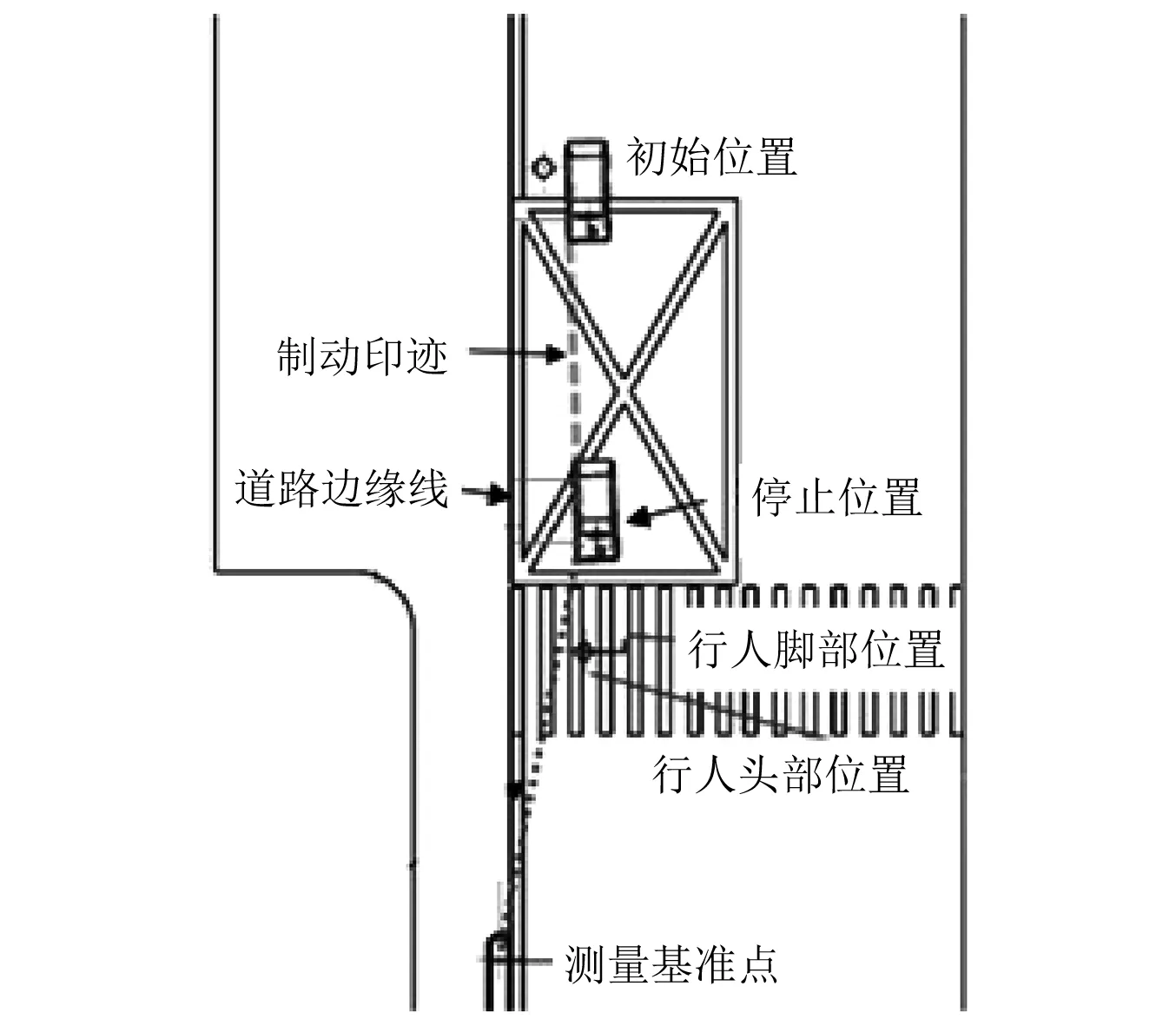
图1 事故现场示意图

建立事故车辆和道路三维数值模型，其中道路为刚性平面，车辆为有限元模型。车辆模型包含8 745个节点，7 459个单元，单元类型包括三角形单元和四边形单元。提取模型的单元信息，在多刚体动力学软件MADYMO中标定车辆几何模型，再结合MADYMO假人模型标定车-人-地多刚体系统数值计算模型的参数，车辆参数从车辆数据库的型号中提取。事发时车内乘坐2名成年人的质量为150 kg。根据行人体貌特征，选择PedHumanMale50%分位男性假人模型。该行人模型为多刚体假人模型，基本单元为椭球体。另外，根据相关医学鉴定结果资料，结合行人受伤模式和当事人笔录，确定碰撞前行人的初始姿态。完成后的多刚体系统计算模型如图2(a)所示。

设定计算时间为2.5 s，步长为2×10-5s，采用欧拉积分法，将碰撞前、碰撞瞬间、抛出过程、落地和停止等几个关键时刻行人所处位置及状态集成在图2(b)中，其中的线条代表行人头部运动轨迹。通过与现场勘查记录进行对比，本案例的数值仿真结果较好地还原了事故过程。

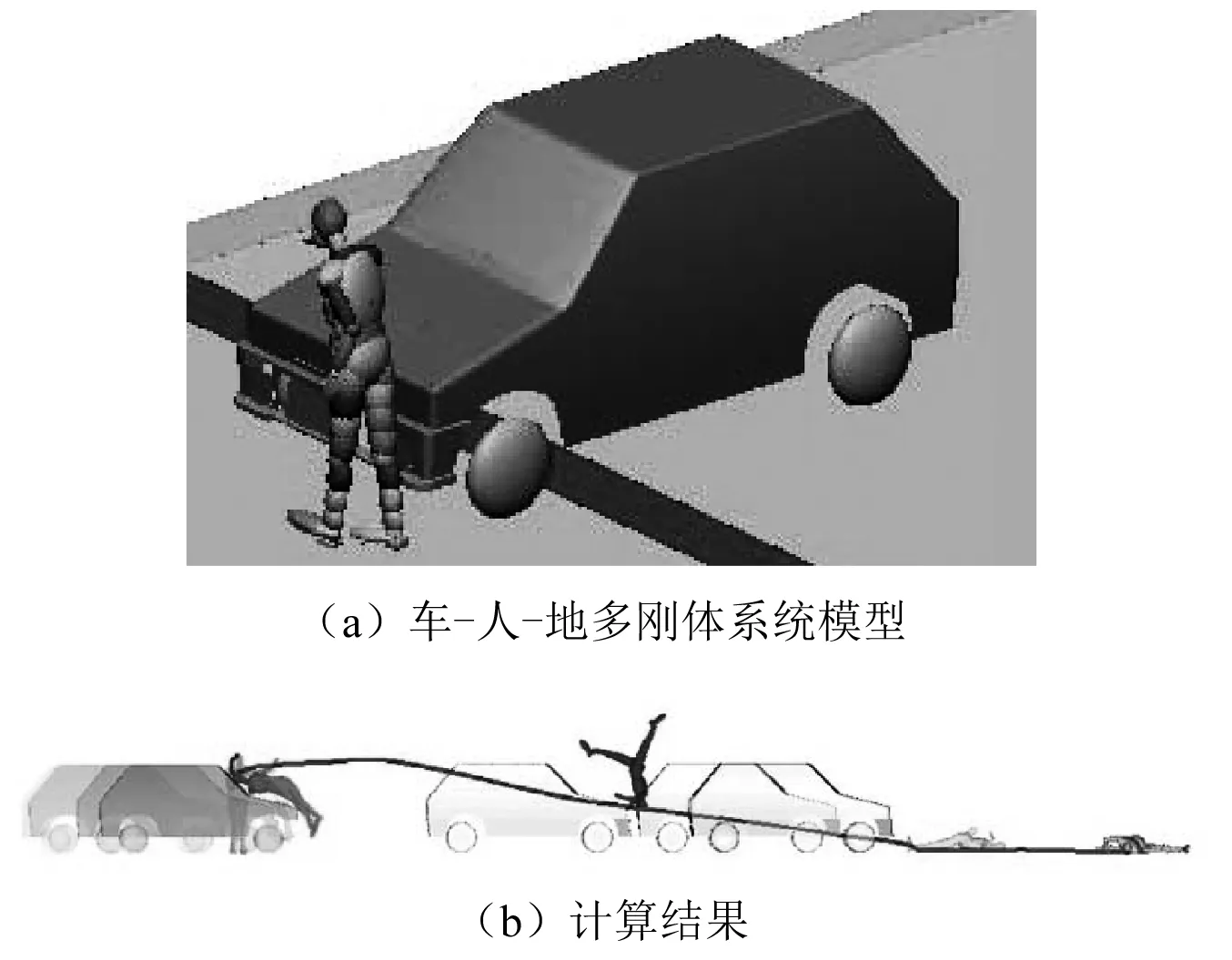
图2 事故建模及过程计算

2 人-地摩擦因数可靠性分析

为了对人-地摩擦因数μp进行可靠性分析，首先建立目标变量与μp间的函数关系。本文将着重考察行人落地姿态和车辆初速度两个目标变量。

经分析，本案中行人运动状态分为两个阶段：落地前和落地后。人-地摩擦因数的作用主要体现于第二阶段。第一阶段中，车辆初速度对行人的运动形式有着决定性的影响，因此，在进行人-地摩擦因数分析之前需要对车速做出较为准确的推算。

2.1 车辆初速度判定

在事故的正向仿真计算中，通常车辆初速度对计算结果的影响比其余参数都更为敏感[8]。车辆初速度判定主要根据现场测量痕迹，包括挡风玻璃破损位置和行人抛距。

一方面，不同车辆初速度下车辆与行人碰撞后，行人侧倒后与挡风玻璃碰撞的位置存在差异。这种差异主要由行人侧倒的角速度和车辆的行驶速度决定。已有的计算分析表明，在车辆常见的行驶速度范围内(30～80 km/h)，行人侧倒角速度对碰撞点位置的影响远小于车辆行驶速度对其的影响；即车辆行驶速度越大，行人头部与挡风玻璃接触时间越早，碰撞前的行人角位移越小，则相应的碰撞点位置也越高。在此形态交通事故中，挡风玻璃破损位置可作为车速推算的依据之一；另一方面，根据碰撞理论，碰撞速度对行人抛距有直接影响，故行人抛距也是车速判定的重要依据。以上数据可通过现场及停车场勘测直接获得。

取速度区间为30～80 km/h，步长为5 km/h，设定计算时间0.2 s，计算步长10-5s，采用欧拉积分法。计算结果数据表明，在挡风玻璃与行人头部发生碰撞的瞬间，行人头部质心的Z坐标会发生突变，具体在头部质心位置-时间曲线上表现为一明显转折点。提取不同车速情形下上述转折点所对应的行人头部质心Z坐标，记为Zhead。此外，在接触碰撞过程中，受头部尺寸的影响，挡风玻璃与行人头部的实际接触位置比头部质心位置略低。记挡风玻璃破损中心Z坐标为Zcnt，计算模型中假人头部作为球体处理，根据球与斜平面接触的几何关系，Zcnt与Zhead具有关系：

Zcnt=Zhead-rsinα

式中：r为假人模型中行人的头部半径；α为行人头部质心和接触点连线同水平线的夹角。

对于行人头部，经估算，r约为0.08 m,α约为26°。在MADYMO结果文件中提取碰撞瞬间行人头部质心的Z坐标，经上述修正，采用有理数逼近拟合得到挡风玻璃破损位置Z坐标与车辆初始速度vc0具有近似关系：

(1)

式(1)拟合确定系数为0.999 5。现场测量挡风玻璃破损位置中心点距离地面垂直距离h=1.22 m，根据式(1)，可得其对应位置车速为51.54 km/h。

改变计算时长，保证计算至行人落地之后。车速越大，行人落地后运动时间越长，故不同的车速将对应不同的计算时间。通过对结果文件可视化分析发现，行人落地瞬间躯干的加速度会出现突变，为此采用躯干下部加速度(TorsoLow_acc)突变位置来推算落地时间节点。根据上述时间节点，记录不同车速下的行人抛距，记为dthrow，对所得行人抛距与车速进行二次拟合，得到车速与行人抛距之间的关系为

(2)

式(2)拟合确定系数为0.994 3。现场可测量痕迹包括车辆右前轮制动痕迹，其起始点位置与行人第一落地点位置在汽车运动方向距离为10.34 m，计算模型中初始时刻右前轮中心点与行人中心相距0.81 m，则行人实际抛距为9.54 m，根据式(2)，其对应的车辆初始速度vc0为46.09 km/h。综合考虑上述两次计算结果，选取计算车速为47.67 km/h。

2.2 μp对行人落地姿态影响的可靠性分析

根据现场测量及目击证人笔录，得到行人落地后的大致位置及姿态如图3所示，其中行人基本姿态为卧倒状，背部朝上。

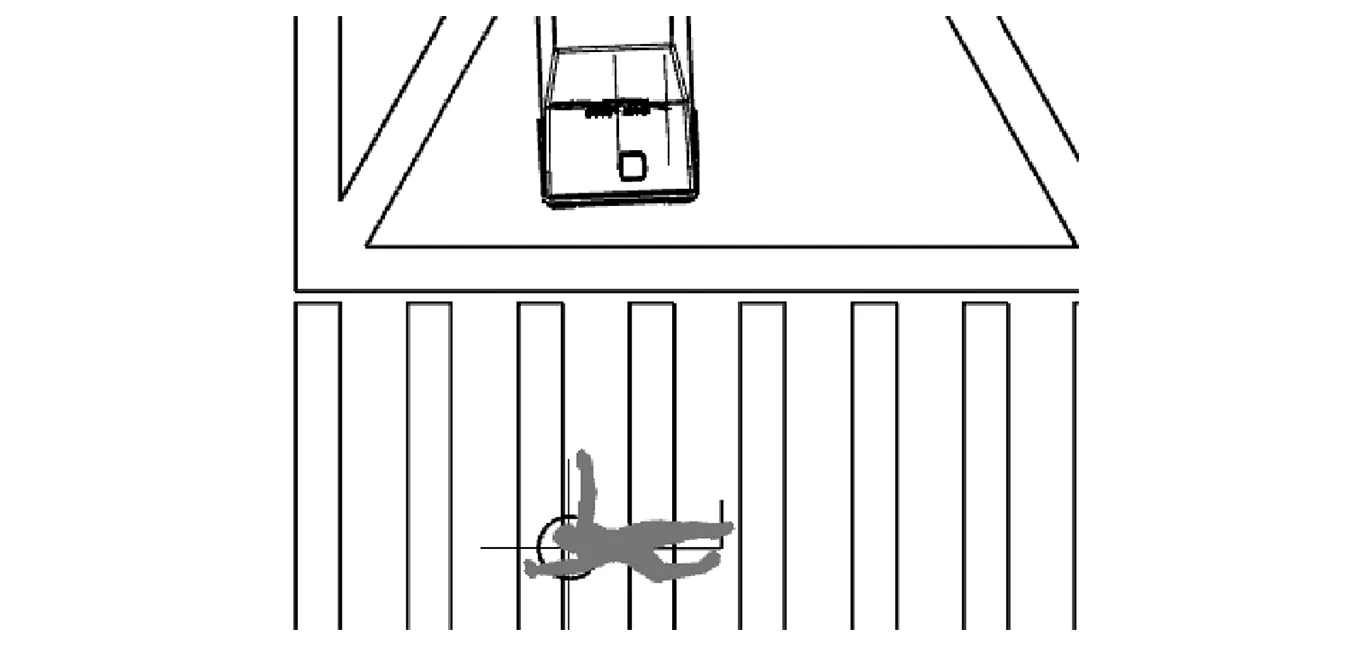
图3 行人停止姿态示意图

为建立可靠性分析的数学模型，首先需要定义计算坐标系。在本阶段过程中，仅考虑人-地摩擦因数对行人运动的影响。此时车辆与行人的接触已经结束，因此对于不同的μp，车辆的停止位置是确定的。为此选择车辆右前轮为原点建立坐标系。如图4所示，xwOwyw为现场测量坐标系，xcOcyc为车辆右前轮为原点的坐标系。A代表行人头部位置，B代表行人脚跟位置，Gp代表行人质心位置。根据现场测量数据，⊙C1的半径为14.23，⊙C2的半径为3.61，xw1=2.30，xw2=2.46，xw3=3.83。由图4可知:

xc1=xw1-xw2,xc2=xw1-xw3

利用圆的方程可以求出行人位置坐标A(-0.160,3.606)，B(-1.530,3.606)以及行人质心位置坐标Gp(-0.845,3.606)。

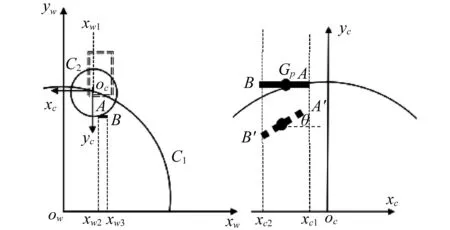
图4 计算坐标系统转换

行人属于多自由度系统，完整描述其状态所需变量较多，为简化计算，本案例中将行人简化为一杆件，其位置信息包括杆件的质心位置和转角，分别代表行人落地质心位置和行人转角，行人转角主要通过测量腹部与头部连线的方向获得。根据现场测量数据类型，定义行人落地姿态向量为

d=(dhead-line,dfeet-line,dhead-tyre,θbody)

式中:dhead-line为头部与边缘线的距离；dfeet-line为脚跟与边线的距离；dhead-tyre为头部与前轮中心的距离；θbody为行人转角。

当质心位置一定时，θbody将影响行人头部和脚部位置，为此考虑将行人转角信息引入前三个变量之中。图4中A′B′为计算所得位置，定义行人长度为

L=xc1-xc2

计算所得质心坐标记为(xG,yG),则行人头部和脚部的坐标分别为

A′(xG+Lcosθ,yG+Lsinθ)

B′(xG-Lcosθ,yG-Lsinθ)

则d中各元素表达式分别为

dhead-line=2.3-xG-0.5Lcosθ

dfeet-line=2.3-xG+0.5Lcosθ

θbody=θ

鉴于质心坐标中已包含转角信息，将行人姿态向量重新定义为

d=(dhead-line,dfeet-line,dhead-tyre)

现场测量得到的准确值记作

则计算结果的相对误差为

式中：M为足够大的整数；k为行人基本姿态标记，k=1代表倒卧，k=-1代表平躺。

定义M与k主要是为了保证行人落地姿态的基本方位。事实上，对于车-人交通事故再现，应当重点关注行人落地质心坐标的精度，上述误差定义中缺乏对这一点的考虑，即当θ发生变化时，对应的误差极小值位置并非是现场测量值，因此需要对d中的元素做相应修正。

取θ∈[-π/2，π/2]，并提取相应ε极小值对应的位置坐标(xmin,ymin)。结果表明θ发生变化时仅ymin发生改变。通过对数据点进行拟合发现ymin与θ具有关系:

ymin(θ)=0.100 3θ3-0.038 73θ2-0.677 9θ+3.617

(3)

式(3)的拟合确定系数为0.999 8。利用该关系对误差函数中的dhead-tyre项进行修正，得到dhead-tyre新的表达式为

其中：

Y(θ)=3.606-ymin

经上述修正，误差极值点位置不再随转角变化而变化，行人停止位置转角仅对计算误差极值大小产生影响。同时，修正后的误差需满足边界条件，即

ε(-0.685,3.606,0)=0

满足上述边界条件的目标函数为

改变人-地摩擦因数，取μp∈[0.55,0.95]。因在仿真计算中发现行人落地后始终呈卧倒姿态，故取消其姿态判断因子。即

(4)

式(4)需要测量的参数包括车辆右前轮坐标系下行人的质心位置(xG,yG)及转角θ。通过直接测量相关节点的相对位置即可获得行人质心相对于车辆右前轮的坐标。考虑到头部转向较为灵活，受外界因素影响较大，故采用胸部与腹部的连线在XY平面上投影点的相对位置来确定行人转角。上述测量节点的具体位置如图5所示。

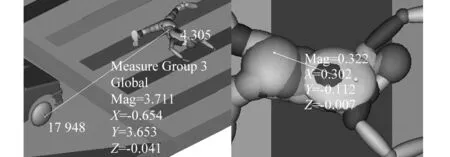
图5 仿真结果数据提取

取人-地摩擦因数范围为[0.56,0.92]，步长为0.01。改变人-地摩擦因数，按照图5所示方法提取不同摩擦因数对应的结果文件数据，代入式(4)计算可得不同人-地摩擦因数下事故再现计算中行人落地姿态的误差值。经尝试，发现采用有理数逼近拟合可得到最为理想的结果，相应的数学关系式为

μp∈[0.56,0.92]

(5)

式(5)的拟合确定系数为0.999 9，所代表的最小误差值为3.4%，对应人-地摩擦因数为0.82。根据上式，绘制如图6所示的人-地摩擦因数的区间与最终行人落地位置误差之间的关系，其中μl与μu分别代表对应误差下人-地摩擦因数的下限和上限。由图6可知，针对本案例，欲将计算误差控制在5%以内，对应摩擦因数取值应在0.78～0.85。同理，10%误差所对应的人-地摩擦因数范围为0.75～0.90。

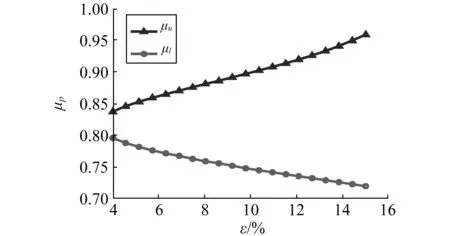
图6 行人落地姿态计算误差与摩擦因数区间的关系

2.3 μp对车速判定影响的可靠性分析

本案例中，行人弹出后沿道路方向合力为零(不计空气阻力)，因此其质心在Y方向的速度会在一定时期内保持恒定，直至落地后与地面发生接触碰撞和相互摩擦滑移。

对于行人质心位置，取车辆初始速度从30 km/h～80 km/h。分析同一车速下的计算结果文件，根据0.3 s～0.9 s之间的计算结果，发现该时间段内行人未落地，因此其在车辆前进方向的位移-时间曲线为直线，表明Y向运动(车辆前进方向)速度基本保持恒定。取t=0.5 s对应的速度，记为vp0.5，考察车辆初始速度与vp0.5的关系。提取不同车辆初始速度下的计算结果，经拟合，碰撞后行人速度vp0.5与碰撞前车速vc0具有关系：

vp0.5=0.2vc0+0.88

上式拟合确定系数为0.976 2。不考虑行人落地后碰撞瞬间的速度损失，行人起始滑移初速度与第二阶段滑移距离s2应当具有关系[9]：

以车辆初速度为47.67 km/h为例，设定重启动计算时间为tr=0.87 s，考察人-地摩擦因数μp对行人滑移距离s2的影响。在计算结果文件中提取相应的数据，经过拟合发现其具有近似关系：

行人作为多刚体模型，受行人姿态的变化的影响，其运动过程与质点在平面滑移不同。在行人落地瞬间各项运动状态参数相同的前提下，人-地摩擦因数对于其之后的运动距离有着显著影响。通过行人地面滑移距离和人-地摩擦因数之间的关系可以发现，对给定摩擦因数做出简单修正后(减小0.295)，其运动规律转换可为传统的单体滑移情形，即μs=常数。本案例中，令

式中：C为待定因子，代入s2=4.19，μp=0.82，vc0=47.67，可得C=0.398。于是针对本案例的一般情形，解得：

(6)

式(6)与道路交通事故鉴定标准给出的经验公式具有相似性。对本案例而言，式(6)则具有更强的针对性。

实际测量中，由于行人路面擦痕测量存在一定的不确定性，实际滑行距离与测量值之间存在一定出入；对于摩擦因数的测量，鉴于环境的复杂性，亦存在一定不确定性。为此考虑行人滑移距离和人-地摩擦因数在某个区间内波动，如服从二维高斯分布，考察上述参数服从一定统计规律下车辆初始速度的分布区间。在后续计算中，为便于表达，令x=s2，y=μp，z=vc0。通过绘制正态概率图发现，当x,y服从正态分布时，z也能较好地服从正态分布，记

z=f(x,y)

则z的期望和方差[10]：

其中x0=4.19，y0=0.82。代入式(6)可得：

E(z)=47.67-0.370 8D(x)-23.616 1D(y)

(7)

D(z)=38.614 2D(x)+2 459.6D(y)

(8)

对于x的方差，其数量级为10-2，对于y的方差，其数量级为10-3，结合式(7)和式(8)中的系数可以发现y对于z的期望和方差有着显著影响，其敏感度约为行人滑移位移的6倍。表明准确测量人-地摩擦因数对于提高事故再现的可信度具有重要意义。

取变差系数为0.1，则变量x和y分别服从分布：

x～N(4.19,0.4192)，y～N(0.82,0.0822)

根据式(7)和式(8)，相应的车速应当服从分布：

z～N(47.45，4.832)

在行人滑移距离和摩擦因数的变差系数均为0.1的情形下，可得车辆初速度95%的置信区间为[42.62,52.27]km/h。因此，在满足上述测量精度的前提下，对于限速30 km/h的判定标准而言，上述结果可作为超速的判定依据。

从另外的角度看，在车速满足上述置信区间的前提下，根据正态分布特点，结合正态分布表可知z>30的概率为

因此，认为此情形下事故车辆超速概率达99.98%。记x的变差系数为C1，y的变差系数为C2。变差系数反映了相应的参数测量精度，其与车辆超速概率之间的关系绘制如图7所示。图7表明变差系数C2对结果影响的显著度明显高于C1，进一步证实了在车-人交通事故再现中人-地摩擦因数的准确测量对于车辆速度判定的重要性。

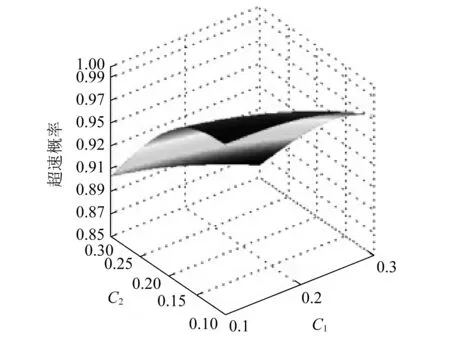
图7 测量精度与超速概率之间的关系

3 结 论

本文探讨了车-人交通事故中人-地摩擦因数对事故再现结果的影响，通过本研究发现：

(1)在车-人交通事故再现中，人-地摩擦因数对事故再现结果精度有显著影响。对某一特定计算误差精度要求，推算出相应的人-地摩擦因数取值范围，由此给出现场勘测的精度要求；人-地摩擦因数对车辆初速度推算也有着极其显著的影响。通过典型案例分析发现，事故再现计算中人-地摩擦因数的敏感度约为行人地面运动位移的6倍。

(2)交通事故再现中，速度结果通常为定值，而摩擦因数也按常数处理。通过典型案例分析，探讨了行人落地姿态计算误差和人-地摩擦因数范围之间的关系。其中，在以行人落地质心为第一考察要素的前提下，需对误差计算模型进行极值修正和边界条件修正。

(3)将摩擦因数作为不确定性参数，探讨车辆初速度结果的合理范围，实现结果由点向区间的转化，给出了所述典型案例的超速概率分析，进一步证实了人-地摩擦因数对事故再现结果的高度敏感性。相应的分析方法可以为交通事故中的车速判断和车-人初始接触位置等关键参数的确定提供依据和参考。