富水软岩流变扰动效应实验及本构模型研究

于永江， 刘 峰,2， 张 伟， 张国宁

(1.辽宁工程技术大学 矿业学院，辽宁 阜新 123000; 2.中煤平朔集团有限公司，山西 朔州 036006)

富水环境下深部矿井软岩巷道呈现出明显的流变特征，具有流变变形大，变形速率快，失稳规律复杂的特征，尤其是受到断层活化、采掘活动、打眼放炮、地震等产生的动力扰动影响后，常常会引发矿井发生蠕变型冲击地压，对煤矿软岩巷道支护设计提出更严峻的挑战。因此，准确掌握富水软岩在动力扰动下的蠕变特性及本构模型是解决软岩巷道支护问题的关键。目前，岩石的流变理论研究多集中于试验研究和本构理论研究，而在流变本构理论研究中大多数学者青睐于模型理论研究，原因在于模型理论中本构关系形式简单、概念直观、参数物理意义明确、可模拟多种力学效应。巨能攀等[1]针对不同含水条件下红层泥岩的蠕变特性，提出一个黏弹性模量，并引入了一个非线性黏塑性体，得到一个改进的伯格斯模型；李鹏等[2]通过对不同含水率条件下的砂岩软弱结构面进行剪切蠕变试验，考虑到加载历史的影响，对蠕变曲线进行了修正；于超云等[3]基于传统的西原模型，引入两个分别与含水率和时间有关的损伤变量，建立了考虑软岩含水劣化效应的本构模型；王俊等[4]利用自主研制的蠕变试验系统，对不同含水率和温度下的深部软岩进行了分级加载实验，系统研究了水与温度作用对软岩蠕变力学特性的影响规律。杨彩红等[5]从微元体的角度分析了水对软岩蠕变性态的影响，建立了单相流体在蠕变变形多孔介质中流动时的固流耦合模型。李江腾等[6]用分级增量加载方式对饱水板岩试样和干燥板岩试样进行蠕变试验，分析了水对具有横观各向同性板岩蠕变特性影响规律。高延法等[7-9]提出了岩石流变扰动扰动效应，研制出RRTS-II 型岩石流变扰动效应试验仪，提出岩石强度极限邻域，得出岩石只有处于该邻域内，扰动效应才能起到显著作用。王波等[10]在已有岩石流变扰动效应、强度极限邻域等概念的前提下，依据实验得到不同流变阶段累积扰动变形量-累积扰动能量曲线，通过拟合得到岩石流变扰动本构方程。崔希海等[11-12]对红砂岩和软弱泥岩进行了岩石压缩流变、岩石压缩扰动流变和岩石拉伸扰动流变试验研究，表明岩石每次扰动均会产生相应的突变变形，且与扰动荷载大小、应力水平和岩石的变形史有关。付志亮等[13]通过实验研究了岩石在循环冲击扰动荷载作用下的蠕变变化，进而研究了岩石的重力冲击扰动损伤特性。黄明等[14]以扰动状态理论为基础，确定了以塑性变形为变量的扰动因子函数，并通过塑性变形随时间的变化特征进一步建立了以时间为自变量的蠕变扰动因子演化方程，并建立基于扰动状态理论的蠕变本构模型。李帅等[15]利用自制的岩石松弛-扰动实验装置，对不同含水率砂岩的松弛过程动态扰动的影响进行研究。

综上所述，前人的研究成果多集中于两方面：一方面考虑含水率的蠕变特性及其本构模型研究，另一方面考虑动态扰动的蠕变特性及其本构模型研究。然而深部矿井巷道在缓慢蠕变过程中经常同时受到水及动力扰动的影响，现有理论不能准确描述软岩在这两种因素影响下蠕变特征。同时，关于含水软岩在动力扰动下变形机制及本构模型的研究鲜有报道。因此，采用自主研发的岩石流变扰动效应实验仪，对不同含水率的软岩进行分级加载流变扰动实验，建立富水软岩流变扰动效应的本构模型，为正确描述富水软岩在动力扰动下蠕变特征及破坏机理的研究提供参考。

1 岩石流变扰动效应实验

1.1 实验设备

试验采用自主研制的岩石流变扰动效应试验系统，见图1。该系统主要包括自主研发的流变支架仪、扰动荷载加载装置、轴压荷载加载装置、数据采集系统等。

(1)轴压加载装置：通过在砝码盘中放入不同重量的砝码，来实现轴向荷载的分级加载。通过运用杠杆原理，使轴向荷载扩大比为45。

(2)扰动加载装置：原理是在固定砝码盘的流变支架上固定一个牵引电磁铁，并且在牵引电磁铁的下部悬挂一个重锤，然后通过时间继电器对牵引电磁铁进行断电控制，从而对重锤升降进行自动控制，以达到对流变支架自动施加冲击扰动的效果。通过冲击后流变支架的振动，产生不同频率与振幅的简谐振动波。

(3)数据采集系统：光耦接口设计与计算机构成的监控系统，便于数据采集、信息传递、远程操控等。系统中配有的KJF25型压力与位移自动监测系统可以与任意型号的传感器进行连接。

1.2 试件制备及实验方案

在某矿的软岩巷道选取了此次实验所用的软岩，将其加工成50 mm×100 mm的国际标准岩石试件(图2)，为保证实验结果分析的可比性尽量在同一大块岩石上密集钻取。由于在钻取试件时会产生较大的热应力，所以通常采用水钻法钻取，并将所钻取的试件放入温度为105℃～110℃的烘干箱内烘干24 h，随后把烘干的岩石试件取出，放入干燥器内冷却至室温。根据岩石天然含水率测定方法测得所钻取岩石试件的含水率为5%，为了研究不同含水率下岩石的流变扰动效应，须将试件制备成至少三种以上的含水率。因而把部分试件浸泡在水槽里，通过不同的吸水时间，制备成含水率为12%和24%的试件。

图1 岩石流变扰动效应实验仪

岩石流变扰动效应就是使原本处于静荷载下的岩石受到扰动后引发的一种永久性变形。为了使这种变形效果更加明显，在实验中分别做了有扰动和无扰动下富水软岩的流变实验。实验通过自主研发的岩石流变扰动试验仪，采用分级加载和扰动加载共同作用的加载方式来完成，对所制备的含水率ω为5%，12%，24%软岩试件进行单轴流变扰动试验。为了确保每次施加的扰动荷载都能对岩石试件产生永久性变形，根据高延法教授提出的岩石强度极限邻域确定此次实验中的分级加载荷载，分别为32 MPa、48 MPa、64 MPa，在同一试件上从小到大逐级施加荷载，每一级荷载的持续时间约为8天，之后再施加下级荷载。施加轴向荷载后一般需要80 h岩石才能达到稳态阶段，随之每间隔200 s对岩石施加一次扰动，扰动作用时间大约为1.5 s，用应变仪每4 h记录一次扰动作用下产生的应变变化，当试件蠕变变形稳定后便进行下次扰动，依次循环往复施加扰动，其中扰动荷载等于牵引电磁铁自由落体时的冲击荷载，扰动次数在1～10次范围内，只有当岩石发生加速破坏后，才停止下次扰动，否则扰动到10次为止。整个加载过程中岩石应变的测量方法：首先在岩石试件的中部位置采用正确的粘合剂使应变片沿其纵向粘贴，然后将导线焊接到已粘贴好的应变片上，再按照半桥单臂接桥法接入到DH5922D动态信号测试分析系统中，即可进行应变测量。实验分为18组，每组4块，共计72块岩石试件。其中9组用来做无扰动下不同含水率岩石的流变实验，剩余9组做有扰动下不同含水率岩石的流变实验。

1.3 实验结果分析

图3为富水软岩扰动前后流变对比曲线，可以看出不同含水率下的流变曲线扰动前后应变发生明显变化，每一次施加扰动的瞬间软岩都会出现变形突然增大，随后该变形值会有不同程度的回弹，最后在此基础上变形持续发展，但最终岩石变形速率趋近于一个稳定值。在每一级荷载加载过程中随着含水率的增加，岩石的瞬时变形量和衰减流变段曲线的曲率半径都增大，且由衰减阶段进入稳态阶段的时间就会延长；整个流变变形全过程中若没有发生加速流变时，就以稳态速率一直发展下去，若发生加速流变时，流变变形速率会大幅度增加，且此时的流变速率大于衰减阶段的流变速率。

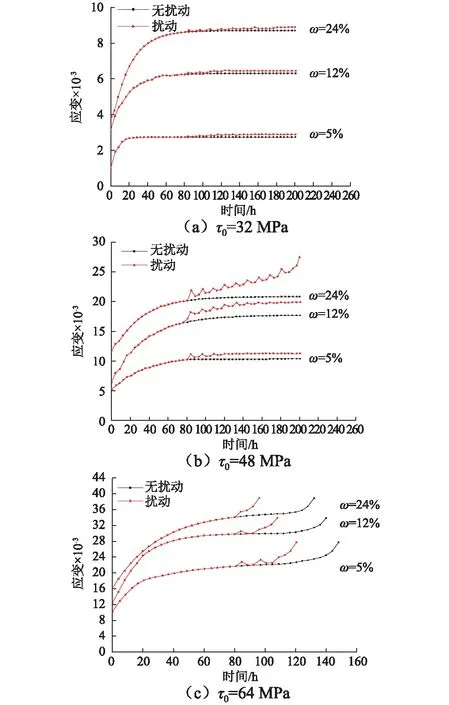
图3 富水软岩扰动前后流变对比曲线

当轴向荷载为32 MPa时，施加扰动后富水软岩的应变变化量相对较小，并且含水率的大小在流变扰动曲线中表现的不太明显。此外，在该轴向荷载下，对不同含水率的软岩进行10次扰动后，发现均未达到岩石流变的加速破坏阶段，说明此时软岩处于非稳定蠕变的稳定阶段，软岩变形无限增长直至发生破坏。当轴向荷载为48 MPa时，与前一级荷载下的流变扰动曲线相比，应变变化量相对较大。同时随着含水率的增加，软岩在扰动下的应变变化量也越来越大，在含水率为24%时，岩石经过10次扰动后出现了加速破坏现象，这是由于每次施加的扰动载荷都能对岩石产生永久性变形，且在多次扰动后，每次产生的应变变化量会进行积累，能量也随之积累，一旦积累的应变值达到岩石破坏的应变值，岩石试件突然发生破坏。而含水率较低的软岩试件未出现加速蠕变阶段。当施加的轴向荷载为64 MPa时，由于在无扰动的情况下，岩石就能发生加速流变阶段，所以对其进行扰动后，应变变化量特别明显，极大地缩短了岩石试件发生破坏的时间。含水率为24%的软岩试件在施加一次扰动后，岩石迅速发生破坏，而含水率较低的试件经过几次扰动后才进入加速破坏阶段。这说明软岩在水化作用后强度降低，极易发生蠕变破坏。

为了使曲线描述效果更加直观，仅对含水率为5%各级轴向荷载下的扰动能量-累积应变及轴向荷载为48 MPa不同含水率下扰动能量-累积应变进行分析。见图4、图5。此次实验中悬挂在牵引电磁铁上的重锤质量为5 kg，自由下落的过程中重锤将重力势能转化为对岩石试件的扰动冲击能量，根据物体的冲击能量计算公式：

(1)

式中：m是重锤的质量，v是重锤自由落体的速率。其中，v=gt，F=mg，g是重锤自由落体的加速度，可得

(2)

通过式(2)计算得出一次扰动后重锤的冲击能量为490 N·m，对于扰动次数在2～10次之间的扰动能量值，按照每一次扰动能量值进行算术方法叠加。

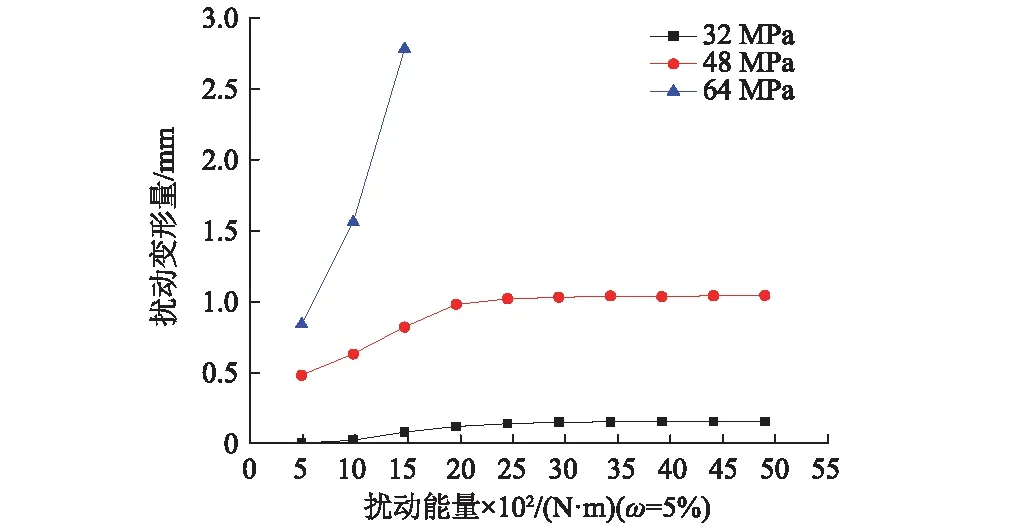
图4 各级轴向荷载下的扰动能量-累积扰动变形量曲线

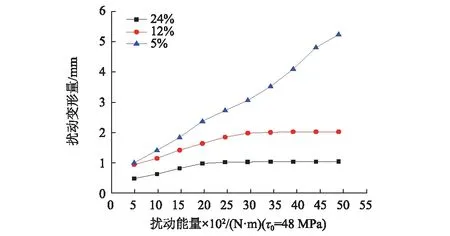
图5 不同含水率下扰动能量-累积扰动变形量曲线

从图4中可以看出，岩石在分级加载时，前两级荷载下的累积扰动变形量随着扰动能量的增加而增加，且增加速率呈递减趋势，当扰动能量到达一定值时，扰动变形速率逐渐趋近于一个恒定值，并持续发展下去。而在第三级荷载下，扰动变形量因扰动能量的增加呈直线上升，直至岩石试件完全破坏。从图5可以看出，当含水率为5%和12%时，曲线形态与分级加载时前两级荷载作用下的曲线形态基本相似， 含水率为24%时的曲线形态除了比第三级荷载作用下的曲线形态平缓一些，其曲线走向基本变化不大。说明富水软岩的流变扰动效应，不仅与轴向荷载和含水率有关，还与扰动能量有关，岩石在分级加载时，荷载达到强度极限邻域内，如果含水率越低，施加的轴向荷载越小，扰动对其流变扰动效应的敏感性较弱，反之，扰动对富水软岩的流变扰动效应的敏感性较强。

2 扰动状态方程

通常把描述材料从相对无扰动态转化为相对完全扰动态的过程，用扰动状态方程D来表示。由于材料的损伤、裂纹的扩展都具有方向性，因此扰动状态方程D是一个具有方向的张量。其表达式根据典型的应力-应变响应可表达为：

(3)

式中：σn为相对无扰动态中的部分应力，σn=Eoεo；σo为表观应力，即分级加载的载荷；E0为表观弹性模量；εo为表观应变；σc为相对完全扰动状态中的部分应力，即应力-应变曲线中的残余应力。

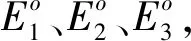
Bazant[16]认为D可以用Weibull分布来描述，并把塑性应变累积值作为自变量，其函数关系式为：

D=D(εp)=Du{1-exp[(-Mεp)N]}

(4)

经化简可得：

(5)

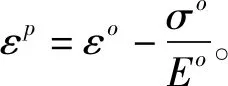
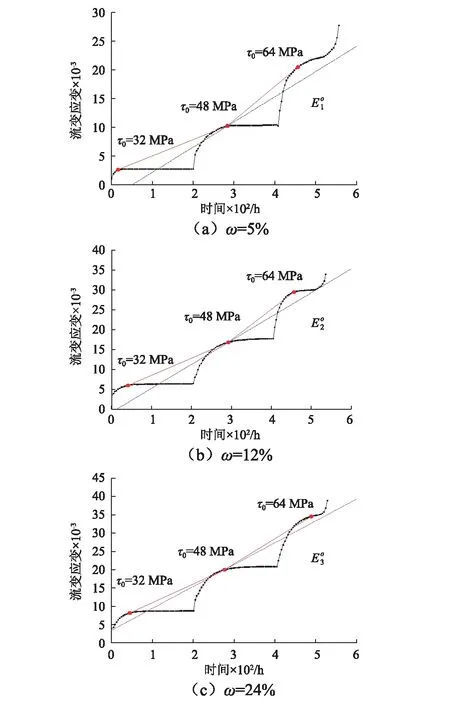
图6 分级加载下不同含水率的流变曲线

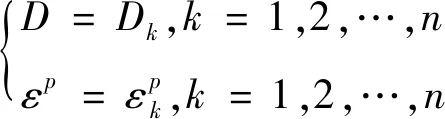
(6)

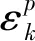
由于在实验结果分析中发现，扰动变形与扰动能量相关，εp可以进一步表示为：

εp=f(ΔW)

(7)

εp=f(ΔW)=a·exp(-ΔW/b)+c

(8)

式中：a，b，c仅为拟合系数，无实际的物理意义。根据软岩的扰动流变特性去Du=1，联立式(5)和式(7)可得，

D=D(εp)=D[f(ΔW)]=1-e[-M·f(ΔW)]N

(9)

3 富水软岩的流变扰动本构模型

基于富水软岩的非线性剪切蠕变模型研究[17]，以及结合本文富水软岩的流变扰动效应实验结果及流变特性分析，需要建立一个描述富水软岩流变扰动效应的本构方程，因而引进扰动状态方程D。根据应变等效假设基本原理，将表观应力需转化为有效应力，用适当的扰动状态方程完成转化。

τ=(1-D)τ0

(10)

式中：τ0为表观应力；τ为有效应力。

依据强度极限邻域，将富水软岩流变扰动效应的本构方程分为以下两种情况：

当τ0≤τs时，

(11)

表1 扰动能量与扰动变形量的实验数据(ω=12%，τ0=48 MPa)

式中：u为岩石的流变变形量；G1为瞬时剪切模量；G2为黏弹性剪切模量；τs为岩石屈服强度；η1和η2均为黏滞系数；t为流变经过的时间。

当τ0>τs时，

(12)

式中：B0、B1、B2及n均为改进的NRC模型参数，其中B0为反映剪应力水平对黏滞系数影响的特征参数；B1为与含水率有关的加速蠕变因子；B2为与含水率有关的稳态蠕变因子。tp为稳态流变向加速流变过渡的起始时刻，tFR为岩石发生破坏时刻，

4 模型参数确定及识别

基于富水软岩的流变扰动效应实验结果，采用BFGS算法以及通用全局优化法的数学优化软件1st Opt对图3中的不同含水率扰动曲线进行辨识，得到富水软岩流变扰动效应本构模型相关参数(见表2)。为了验证所建模型的正确性与合理性，必须使模型拟合曲线与实验曲线进行对比，本文限于篇幅，只给出了图7所示的轴向荷载为48 MPa，含水率为12%时，富水软岩流变扰动效应的模型拟合曲线与实验结果的对比曲线，和图8所示的轴向荷载为64 MPa，含水率为5%时，富水软岩流变扰动效应的模型拟合曲线与实验结果的对比曲线。从图7和图8可以看出，模型拟合曲线与实验结果均吻合的相当理想，不但表明所建立的富水软岩流变扰动效应本构模型的正确性与合理性，而且可以很好的掌握在不同含水率下的软岩受扰动后的流变特性。

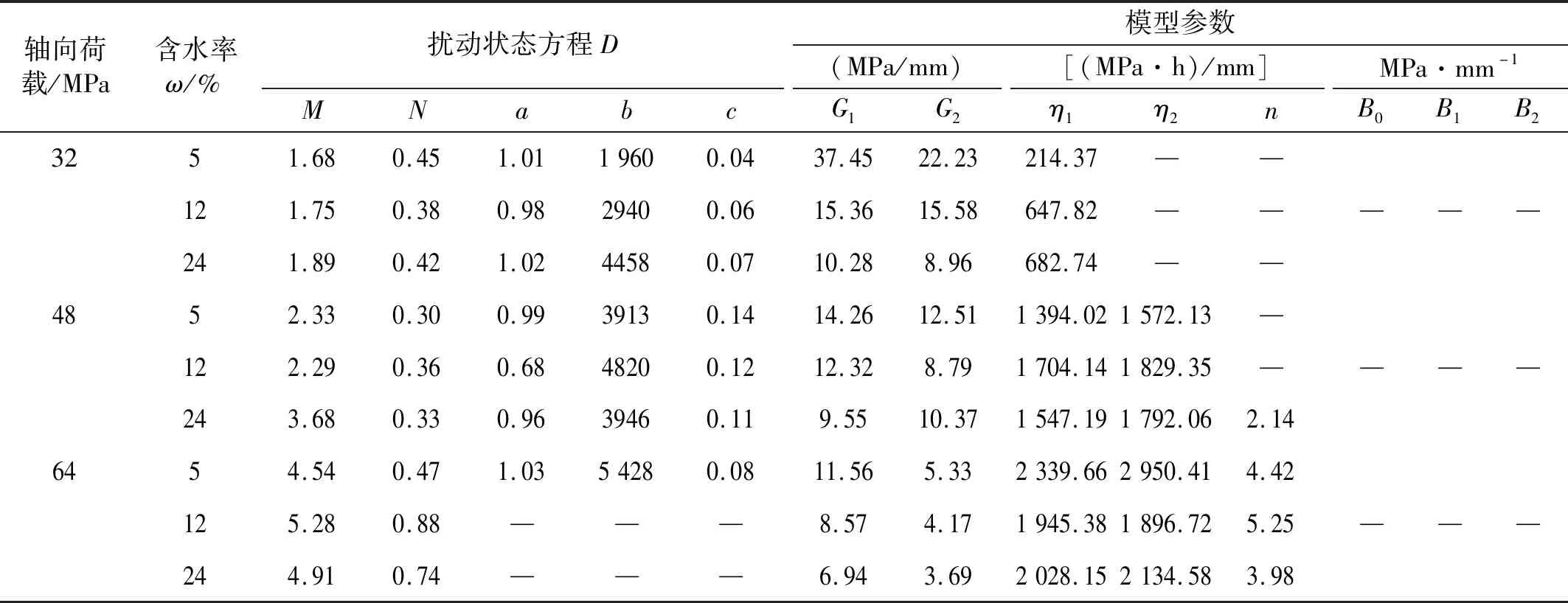
表2 富水软岩流变扰动效应模型参数

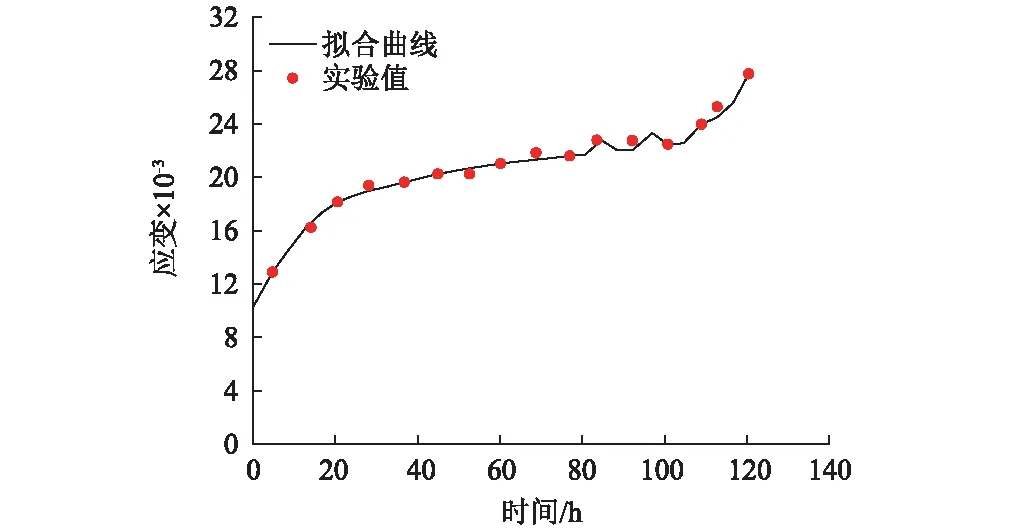
图7 含水扰动蠕变模型和实验结果对比(τ0=48 MPa，ω=12%)

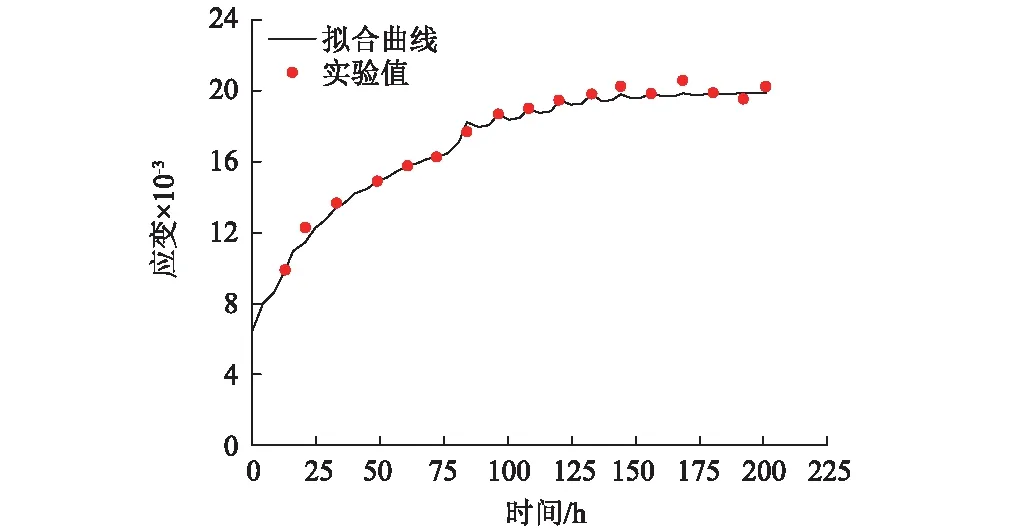
图8 含水扰动蠕变模型和实验结果的对比(τ0=64 MPa，ω=5%)

5 结 论

(1)对不同含水率的软岩进行分级加载流变扰动时，扰动前后流变曲线应变发生明显变化，每一次施加扰动的瞬间软岩都会出现变形突然增大，随后该变形值会有不同程度的回弹，最后在此基础上变形持续发展，但最终岩石变形速率趋近于一个稳定值。同一轴向荷载下，随着含水率的增加，岩石的瞬时变形量和衰减流变段曲线的曲率半径都增大，且由衰减阶段进入稳态阶段的时间就会延长；整个流变变形全过程中若没有发生加速流变时，就以稳态速率一直发展下去，若发生加速流变时，流变变形速率会大幅度增加，且此时的流变速率大于衰减阶段的流变速率。

(2)经过多次扰动后发现，当轴向荷载较小时，含水率的大小在流变曲线中表现的不太明显，岩石流变会一直处于非稳定蠕变的稳态阶段；当轴向荷载较大时，由于每次扰动变形量的积累，使原本处于稳态阶段含水率较大的岩石出现了加速破坏现象，使原本在无扰动下就能发生加速流变阶段的岩石，极大缩短了发生加速破坏阶段的时间。

(3)当应力水平较小和含水率不高的情况下，扰动变形速率随着扰动能量的增加而缓慢增大，当应力水平较高和含水率较大时，扰动变形速率随着扰动能量的增加快速增大，使岩石试件迅速破坏。

(4)依据材料的扰动状态理论，确定了扰动状态方程D，以此为基础，因岩石的流变扰动效应与扰动能量紧密相关，通过非线性拟合的方法，将扰动态方程D又进一步演化成以扰动能量为自变量的函数。根据应变等效假设基本原理，将扰动状态方程D与富水软岩的非线性剪切流变模型进行有机结合，建立了富水软岩流变扰动效应本构模型。

(5)采用精确可靠的BFGS算法和数学优化软件1st Opt对实验曲线进行辨识，得到本构模型的相关参数，同时用实验数据去验证所建立的模型，结果发现实验值与模型拟合曲线吻合效果良好，证明了富水软岩流变扰动效应本构模型的正确与合理性。