极端地震下惯容器-弹簧-阻尼装置对隔震结构减震效果研究
2019-07-08莊初立五十子幸树张永山
莊初立, 五十子幸树, 张永山
(1. 广州大学 土木工程学院,广州 510006;2. 日本东北大学 灾害科学国际研究所,日本 仙台 980-0845)
近年来巨大地震造成超高层建筑和隔震建筑位移响应过大,2011年日本东北大地震中,在宫城县检测到的最大隔震支座位移达到41.5 cm[1],因此采用带阻尼器的隔震系统进行混合控制显得尤为必要,防止当发生超过设防标准地震时能有效控制隔震层位移和楼层加速度。
过去的研究表明,附加耗能装置能有效减轻地震响应,在高层建筑和隔震建筑中得到广泛应用,且耗能装置多样[2-3]。近年来一些基于惯容器的新型耗能装置也相继提出来[4],在建筑结构控制领域逐渐受到关注,其增效机制主要利用滚珠螺杆、齿条和齿轮、或者杠杆摆,可以产生几十到数千倍于物理质量的表观质量。Arakaki等[5]研发了RDT装置,通过滚珠螺杆将轴向运动转成内部和外部转筒的相互转动,这种装置能将内筒旋转方向的位移放大为轴向位移的5倍~40倍。Saito等[6-7]将黏滞阻尼单元与质量单称为TVMD。为了确定TVMD的最优参数,Ikago等[8]利用定点理论推导了单自由度体系附加TVMD的最优频率比和最优阻尼参数的封闭解,也验证了TVMD的控制性能优于线性黏滞阻尼器。Kikuchi等[9-10]提出一种将弹簧单元、阻尼单元和质量单元串联配置的质量黏滞阻尼器(ISD),改良既往FRVMD对加速度的减震效果,同时验证了改进后ISD的有效性。李超等[11]针对TVMD采用定点理论和遗传算法进行参数优化研究。邱吉祥等[12]将TVMD附于单质点钢结构,分析了在简谐波作用下TVMD的减震性能以及适用场合。
本文将对附加在隔震层的ISD装置构造参数优化目标函数,基于定点理论推导ISD最优参数的封闭解。既有文献[13]以体系位移与地面加速度之比为目标函数进行优化,同样采用了定点理论推导了单自由度体系下ISD的优化公式,而本文与之不同的是以体系位移与地面位移之比为目标函数进行优化,下文对两种方法的结果进行了比较。最后将ISD作为极端地震时控制楼层加速度的装置来考虑,通过算例探讨在极端地震作用下ISD装置的控制效果。
1 惯容器-弹簧-阻尼系统
串联型的惯容器-弹簧-阻尼(ISD)系统的力学模型如图1所示,其中弹簧部分是起到对主系结构调谐的作用,质量单元起到放大质量效应的作用。
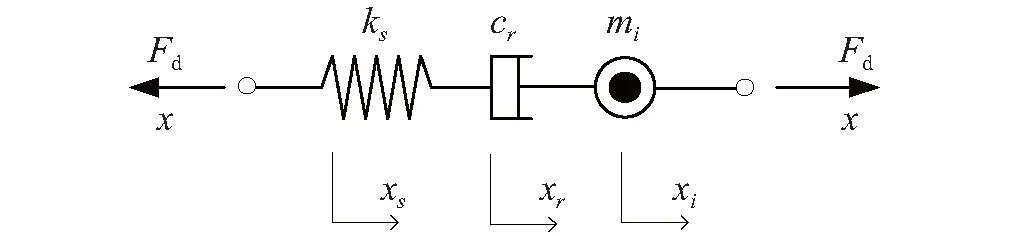
图1 惯容器-弹簧-阻尼系统
为研究ISD的控制性能,将ISD附加在单自由度隔震体系中,如图2所示。其中m和k为主系结构的质量和水平刚度,ks、cr和mi分别为ISD的支撑刚度、等效黏滞阻尼系数和表观质量。
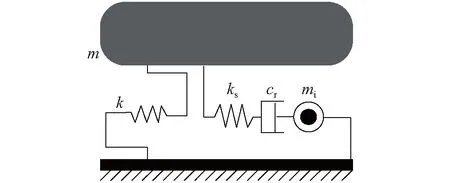
图2 附加ISD的单自由度体系
当系统受到基底激励时,系统的运动方程如下
(1)
式中:Fd为ISD的出力。
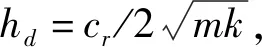
根据上述定义,将各参数代入式(1)可得,单自由度体系位移与地震动位移的幅值比如下式所示,即位移传递函数
(2)
同样可以得到单自由度体系绝对加速度与地震动加速度的幅值比为
(3)
2 基于定点理论的ISD参数优化
根据上述推导的位移传递函数,保持ISD的质量比和频率比不变,考虑阻尼比为0、∞和0.5时的三组工况,进行频域分析的结果如图3所示。图3表明ISD质量比和频率比不变,调整不同的阻尼比时,共振曲线存在两个共同点P和Q,因此,单自由度体系附加ISD时,可采用定点理论进行参数优化。
我的画院:画院坐落在美丽的地方,有很多美丽的故事。如果想到其与宋代有着各种联系,立刻让人感到渺小,又让人振奋,力争创作出美丽的画,以不负各方。
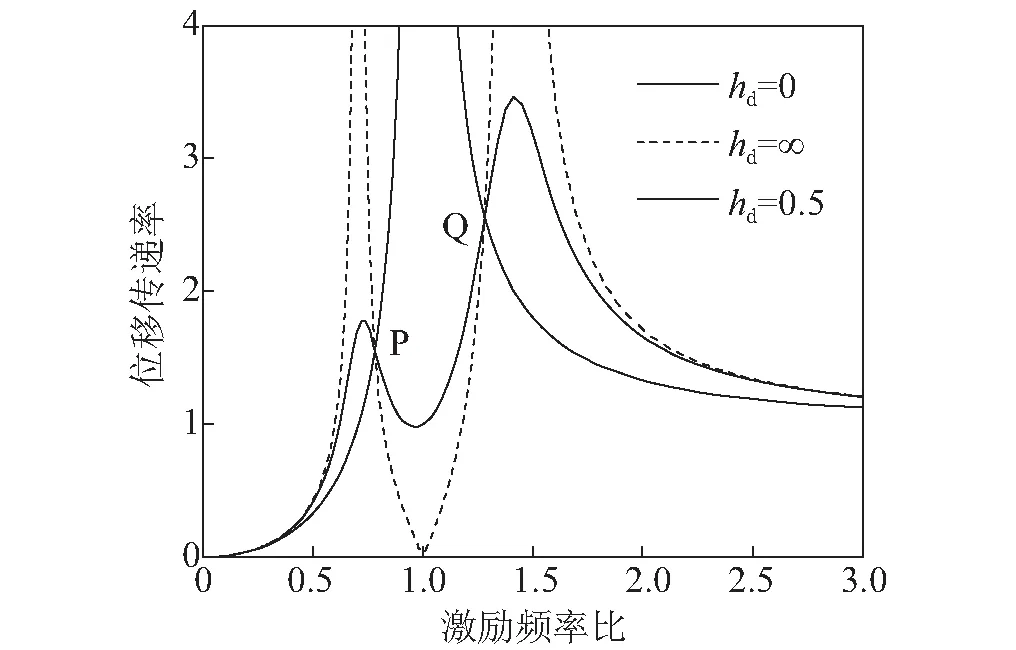
图3 共振曲线
根据定点理论进行参数优化时,需要满足两个条件[14],其一是在P点和Q点的幅值相等,二是共振峰值出现在P点和Q点。本文以位移传递函数为目标函数,根据定点理论进行参数优化,因此,根据定点理论,将hd=0和hd=∞代入式(2)可得。
(4)
(5)
2.1 最优频率比求解
令式(4)与式(5)相等。整理可得
(6)
定义γP和γQ分别为定点P和Q所对应的激励频率比,显然γP和γQ为式(6)的根,因此式(6)可以改写成如下形式
(7)
比较式(6)和式(7)可得
(8)
(9)
将γP和γQ代入式(4)可得
(10)
由式(8)、式(9)和式(10)整理可得
(11)
求解式(11),可得最优频率比βopt如下
(12)
2.2 最优阻尼比求解
根据第二个优化条件,共振曲线在P点和Q点处存在极值,因此优化条件可以写成如下形式
(13)
定义,
(14)
令γ2=Γ, 根据式(13)和式(14),可将优化条件等效表达如下
(15)
将γ2=Γ代入式(14)整理得
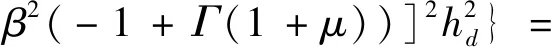
(16)
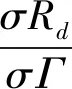
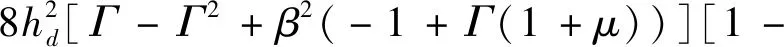
(17)
求解式(17)可得阻尼比的表达式如下
(18)
此外,基于最优频率比式(12),求解式(8)和式(9)可以得到P点和Q点相应的激励频率比。
(19)
(20)
将式(19)和式(20)代入式(4),可得
(21)
将式(12)、式(19)和式(21)代入式(18),可得
(22)
同理,将式(12)、式(20)和式(21)代入式(18),可得
(23)
根据Brock的定义[15],取上述两式平均值并开方,得到最优阻尼比如下
(24)
将本文推导的优化公式与文献[13]中的优化公式(位移振幅最小)进行比较。给定质量比为μ=0.5,采用文献[13]和本文的优化公式分别确定ISD参数,得到位移和绝对加速度放大系数与频率比的关系如图4所示。在频率比大于1的部分区域本文的优化效果远好于文献[13],而在频率比小于1的部分区域则文献[13]的优化效果较好,对全频段的最大值控制来看本文提出的优化公式控制效果更好。
3 ISD控制性能分析
3.1 分析模型
分析模型选用如图5所示的6层隔震结构,各参数如表1所示。隔震层仅考虑隔震支座水平刚度,不考虑隔震支座的固有阻尼,上部结构第一振型的临界阻尼比取2%。基础固定时,上部结构的第一周期为0.37 s,隔震结构的第一周期为4.0 s。假定结构位于8度区,性能目标为极罕遇地震作用下隔震支座位移限制在0.4 m以内。在隔震层分别附加ISD和LVD进行地震时程分析,检验ISD的控制性能。
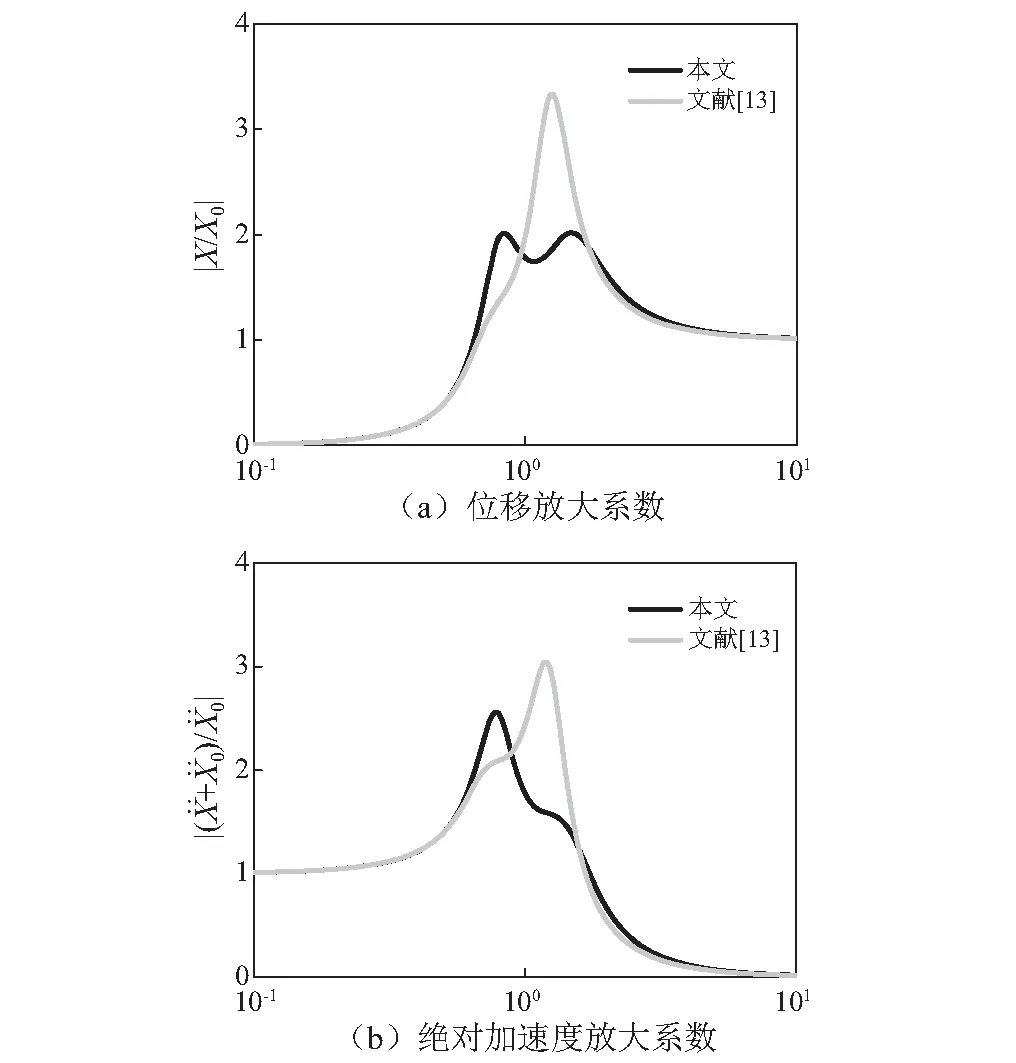
图4 传递函数幅值
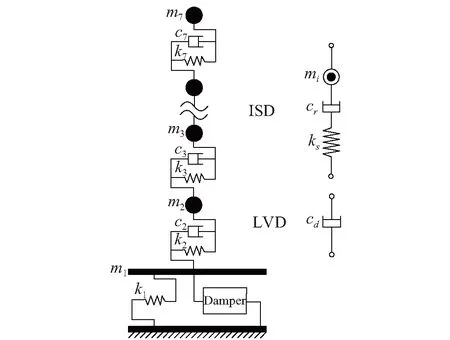
图5 分析模型
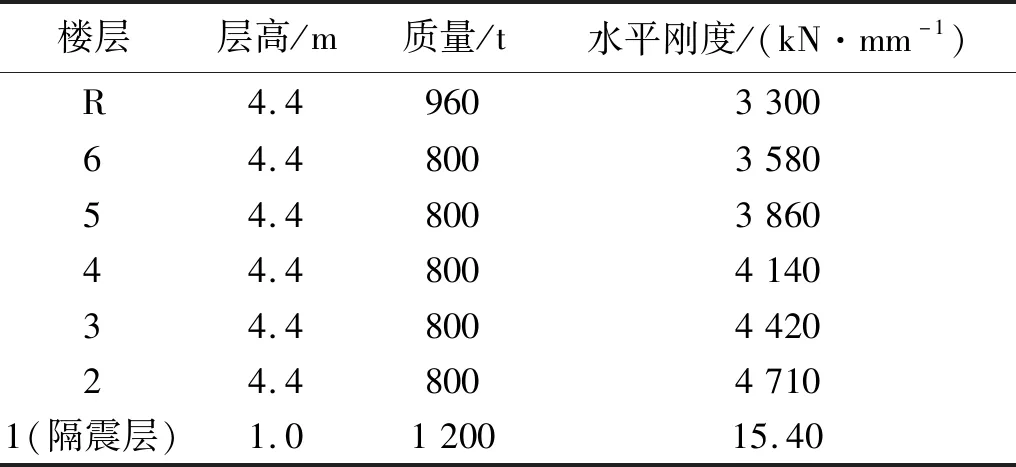
楼层层高/m质量/t水平刚度/(kN·mm-1)R4.4960330064.4800358054.4800386044.4800414034.4800442024.480047101(隔震层)1.0120015.40
3.2 输入地震动
为验证ISD控制的有效性,根据建筑抗震设计规范[16],选用5条不同的天然地震波NW1-NW5和2条人工波AW1-AW2。天然波选自太平洋地震研究中心(Pacific Earthquake Research Center)的强震数据库[17],人工波AW1采用随机相位和设计反应谱对应的加速度时程曲线合成,人工波AW2根据1952年的Taft波EW分量和设计反应谱对应的加速度时程曲线合成。地震动信息见表2,相应的地震动反应谱与设计谱对比如图6所示。根据中国地震动参数区划图[18],输入地震时程加速度峰值统一设置为0.6 g,对应于极罕遇地震。
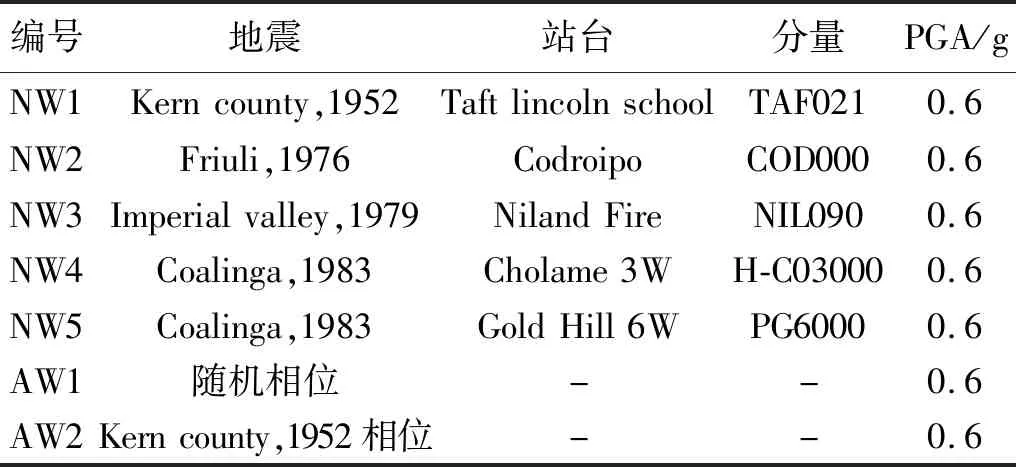
表2 天然强震记录和人工波
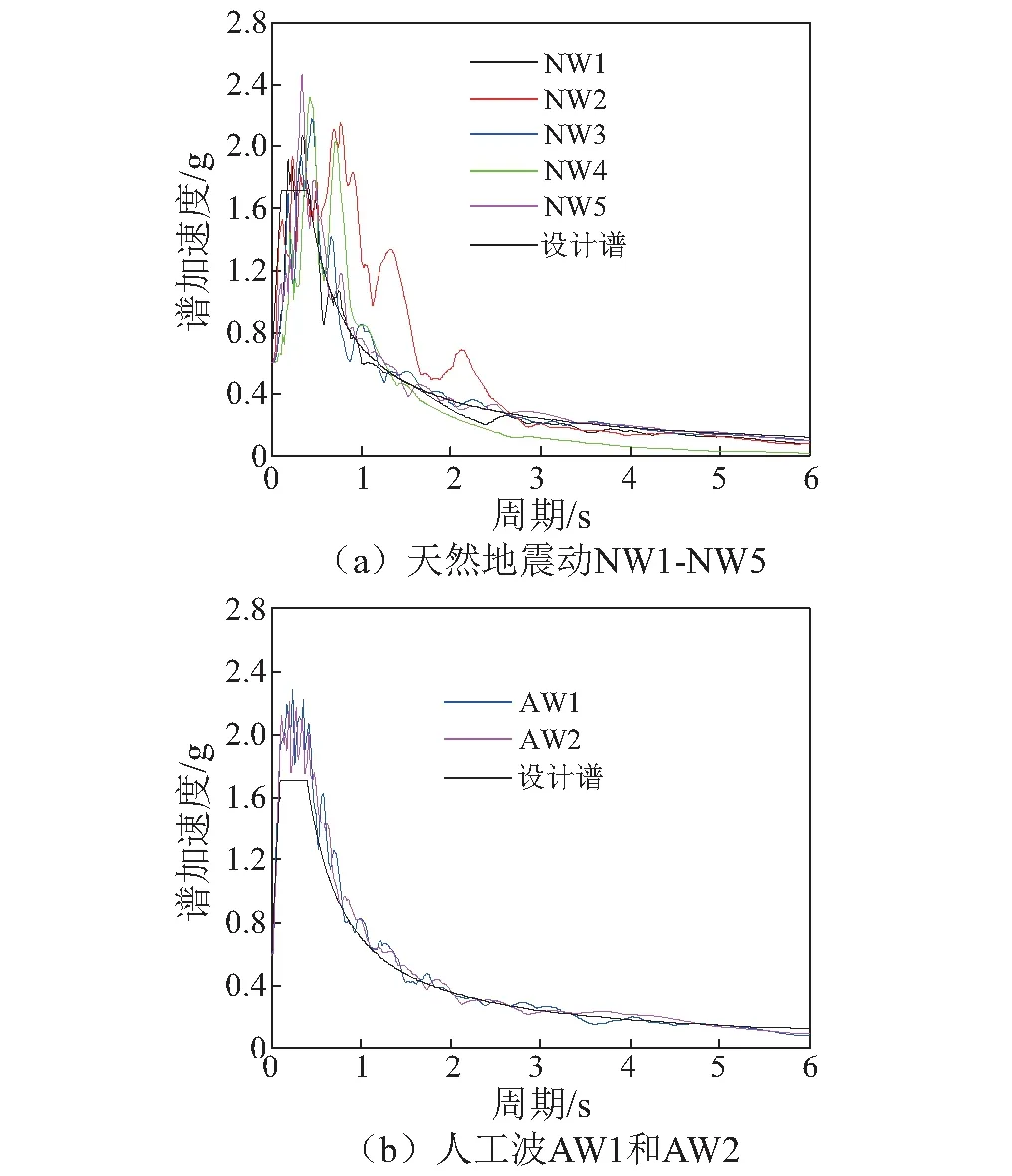
图6 输入地震动反应谱与设计反应谱
3.3 性能对比
给定质量比范围0≤μ<2,质量比按步距0.01取值,然后根据定点理论的优化解公式(12)和式(24)分别确定最优频率比和最优阻尼比,从而进行地震时程分析。LVD阻尼系数的确定,给定隔震层的阻尼比范围0≤h≤0.5,阻尼比按步距0.01取值,然后将隔震结构简化为单质点模型,由公式C=2Mω1h确定LVD阻尼系数,同时引入文献[13]的优化公式进行比较。
由多组工况计算结果绘制出极罕遇地震作用下的性能曲线,如图7所示。取7条地震动的平均值,显示了阻尼器参数的选择对最大顶层加速度与最大支座位移间权衡的影响。从图7可以看出阻尼比和质量比的增加均可以降低隔震层的位移,但增加到一定程度时带来结构加速度的增加,这需要在设计中考虑位移减少与加速度增加两者间的平衡,从而确定系统的最优参数。在设计感兴趣的支座变形区段中可看出(本例在极端地震作用下的支座变形设计值为0.4 m),当支座变形相同时,附加ISD装置的结构顶层加速度小于附加LVD的。从图7可看出本文所推导的优化公式确定的ISD参数所得到的性能曲线好于文献[13]。
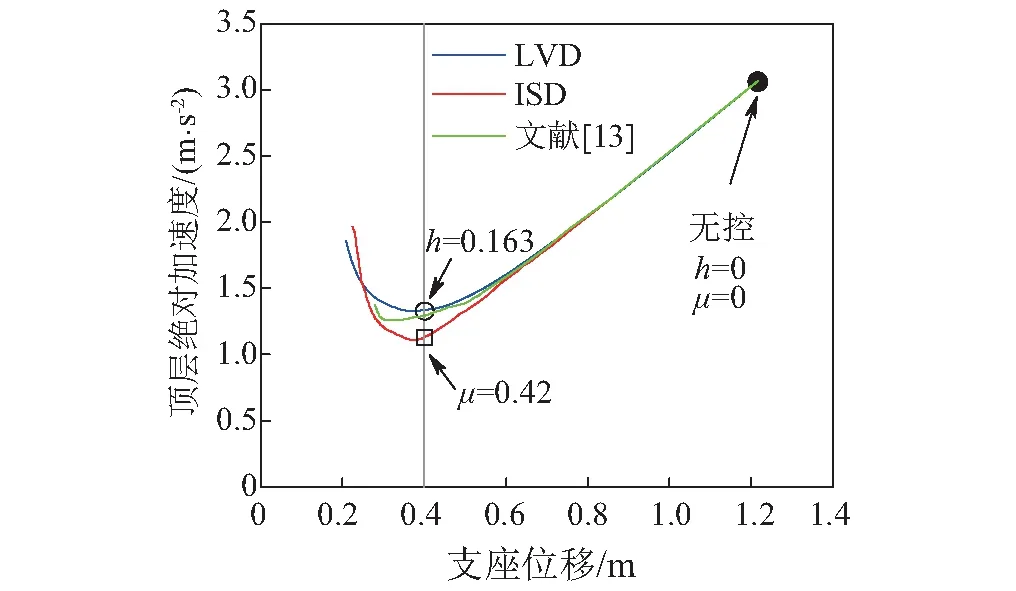
图7 极罕遇地震下的性能曲线
为进一步检验ISD装置的控制性能,假定隔震层变形相同时对比结构其余响应的控制效果。取性能目标控制位移0.4 m时所对应的阻尼器参数进行详细的结果分析,根据图7的性能曲线即可确定各阻尼器参数如表3所示。根据上述性能曲线确定ISD和LVD参数,进行楼层响应结果对比,如图8所示,当相对于地面的楼层位移基本一致时,附加ISD的楼层绝对加速度沿楼层分布大致相同,而附加LVD的楼层绝对加速度在上部有明显的增加倾向,且附加ISD后结构绝对加速度有较明显的降低,降低幅值约为15%;与LVD相比,附加ISD后的基底剪力减小约5.89%,且上部楼层剪力则均比附加LVD的要小,附加ISD的楼层倾覆弯矩均要小于附加LVD的,最大降低幅值为10%。
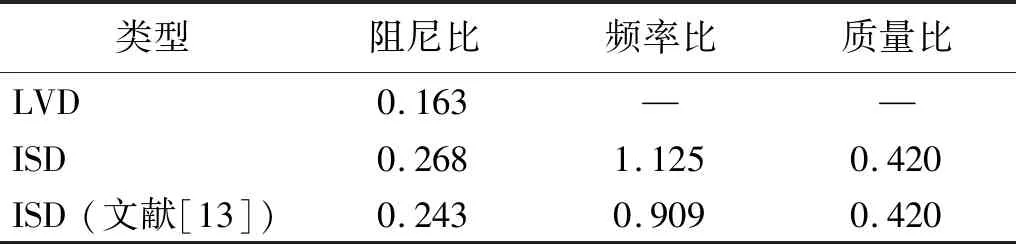
表3 阻尼器参数
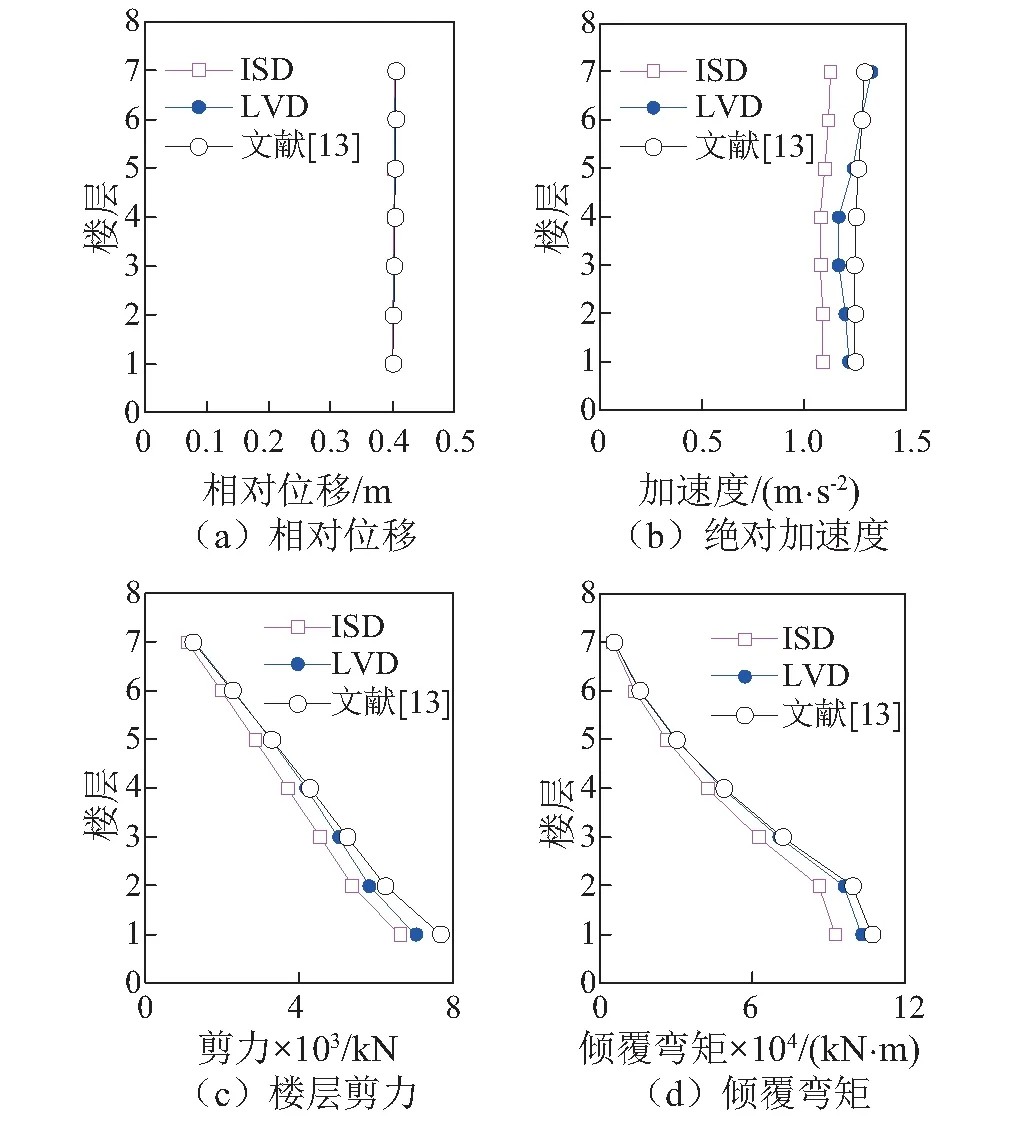
图8 极罕遇地震下的楼层平均响应
4 结 论
本文以位移传递函数为目标函数,基于定点理论进行ISD的参数优化,并考虑将ISD作为极端地震时控制楼层加速度和支座位移的装置,以一栋6层隔震结构为例,根据最优参数的ISD进行极罕遇地震时程分析。结论如下:
(1) 给定质量比,基于定点理论获得了ISD的最优参数封闭解,全频段最大值的控制效果优于既有文献的优化解,改进了优化方法。
(2) 优化目标函数选取的不同影响ISD对隔震结构的控制效果,不同频率比区间的优化结果各有优劣,宜根据实际结构特性和激励选取合适的目标函数进行优化。
(3) 附加ISD的隔震结构,隔震层位移相同的条件下,控制性能优于LVD,在减小隔震层位移的同时也能减轻加速度,也验证了对ISD参数优化设计是可行且有效的,也表明了ISD能较有效地应对极罕遇地震的作用。
(4) 控制隔震结构在极端地震下的位移是设计的首要目标,基于本文优化方法的ISD装置比LVD更能有效的控制隔震层位移和结构加速度,可为隔震结构的大震设计提供有效的控制方法。
