Levy噪声下新型势函数的随机共振特性分析及轴承故障检测

贺利芳, 周熙程, 张 刚, 张天骐

(1.重庆邮电大学 通信与信息工程学院，重庆 400065; 2.信号与信息处理重庆市重点实验室，重庆 400065)

近年来对于弱信号中的噪声，传统的处理方法有奇异值分解(Singular Value Decomposition, SVD)和小波变换(Wavelet Transform, WT)，但是这几种方法在信噪比极低的情况下往往是一种有害而无利的存在。因此，随着Benzi等[1]研究古气象冰川问题时首次提出随机共振，随机共振作为一种新的信号处理方法进入了人们的视野，20世纪90年代，Collins等[2]将信息论和随机共振相结合，提出一种非周期随机共振理论，拓宽了随机共振的应用范围。在非线性系统中，在一定的信噪比范围内，通过随机共振系统把噪声的能量转化为微弱信号的能量，使信号能量加强，这种新颖的方法掀起了人们对随机共振研究的极大热情。

在弱信号检测中，系统模型是随机共振研究的一个重要方面，且噪声环境大多数是高斯噪声，然而高斯噪声是一种理想中的噪声，不能代表自然界非人为活动产生的随机噪声，如动物噪声、深海噪声、气流噪声等等[3-4]都是非高斯噪声，其波形有着显著的脉冲特性和拖尾特性，为了准确地模拟各个领域中的噪声，近几年噪声诱导的随机共振开始引起了学者们的注意，对Levy噪声下系统参数诱导的随机共振研究有极大的进展。Wang等[5]研究了Levy噪声下的FHN模型的随机共振；Liu等[6]研究了在α噪声下的tri-stable系统随机共振特征分析；Zhang等[7]研究了欠阻尼下Pinning型势阱的随机共振系统，并将该系统应用于轴承故障检测中；孙虎儿等[8]研究了级联分段线性随机共振的微弱信号检测，检测效果优于经典的级联双稳系统；王林泽等[9]提出基于随机共振原理的分段线性模型，深入地进行了理论分析与实验研究；冷永刚等[10]探讨了二阶线性系统调参共振特征信号检测；Guo等[11]研究了在加性白噪声和乘性非高斯噪声下的一种新型非线性模型在随机共振中的应用，深入的进行了数值分析和仿真。从上述的势阱模型中，与研究较为成熟的CBSR系统相比，这些势阱模型都具有突出的优势；并且通过理论分析可知，经典的双稳随机共振(CBSR)系统有着与生俱来的输出饱和性[12-14]；这种特性不仅降低了系统对信号的增强能力，还限制了在噪声环境中系统对信号的检测能力，因此，在微弱信号提取和检测中，怎样有效的避免双稳系统的输出饱和性是有必要的。

为了克服这种输出饱和性，提出了一种新颖的分段非线性双稳随机共振系统，并且引入了更加接近工业环境中的非高斯Levy噪声，高斯白噪声就是Levy噪声在特征指数α=2的特殊形式，所以本文研究了在Levy噪声不同α(0<α≤2)和β(-1≤β≤1)下的分段非线性势函数(PNBSR)的随机共振特征分析，以及系统参数l,c,a和b以及噪声强度D对系统共振输出的作用规律；并且在工业生产应用中，当机械设备中的滚动轴承发生故障时，不可避免地要受到来自其他机械设备和工作环境噪声的干扰，故障信号往往被强大的噪声所淹没无法识别。所以近年来，广大学者对旋转机械的故障诊断进行了大量的研究，本文也将所提的PNBSR系统应用于在CWRU轴承故障检测中。

1 PNBSR系统模型和方法

1.1 随机共振系统模型

在微弱周期信号和Levy噪声共同驱动下，忽略惯性项的过阻尼非线性系统模型可以描述为：

(1)

式中：A是微弱周期信号的幅度；f是待测微弱周期信号的特征频率；V(x)为PNBSR系统势函数；D为噪声强度系数；ξ(t)为非高斯Levy噪声。Levy噪声的介绍在1.3节给出。

1.2 PNBSR系统模型

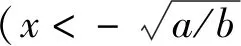
(2)

式(2)中，参数l>0，c>0，a>0，b>0，参数k=2(l+a2/4b)，对势函数V(x)求导，就会得到系统模型的势阱力-dV(x)/dx，表达式如下

(3)

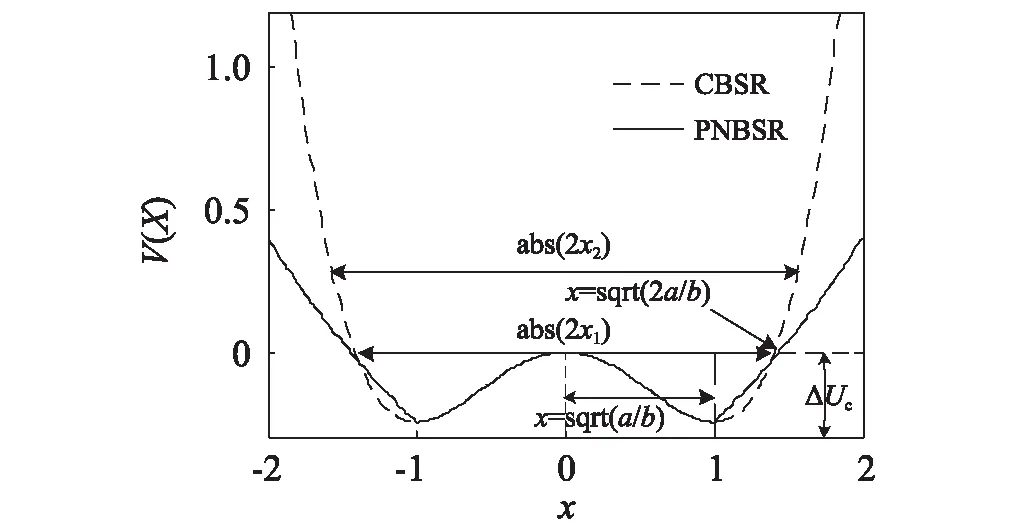
图1 CBSR和PNBSR系统势函数

图2表示的是调节系统参数，系统各个参数对势函数曲线变化的影响，由图可知，改变l或c值时，对势阱壁的陡峭程度影响是非常大的，并且l和c的取值越小时，势阱壁就会越陡峭，取值越大就会越靠近势垒；而由图2中圆圈线和叉线可知，改变a或b值时，对双势阱的深浅产生很大的影响；例如当b=0.4时，a的取值越小时，双势阱的深度就越浅，且当a=0.9时，b的取值越大时，双势阱的深度就越浅，这就造成粒子跃迁所需要的能量小，系统就更容易产生随机共振现象。

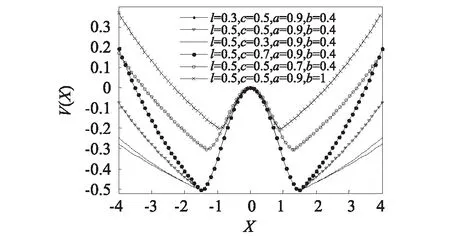
图2 不同PNBSR系统参数下的势函数

为了深入的对PNBSR系统进行理解分析，在理论基础上做了CBSR系统与PNBSR系统的对比；我们可知CBSR系统有两个势阱和一个势垒，同样可知PNBSR系统也有两个势阱和一个势垒，并且势阱壁的陡峭程度仅仅由PNBSR系统参数l和c决定，也就是势阱壁的陡峭程度随着x的增加保持不变，此外势垒高度也是由PNBSR系统参数a,b调节，以此来进一步控制粒子跃迁的速率；通过已有的绝热近似理论可以计算出CBSR系统的克莱莫斯跃迁率[15-16](逃逸率)表达式为：

(4)

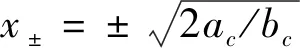
(5)

化简式(5)可得到c值：

(6)

根据等式(2)，由绝热近似理论[17]可知，粒子运动到x±这个状态才能跃迁，所以平均穿越时间τ±[18]可通过等式(7)可计算出:

(7)

要求输入信号满足绝热近似条件：f、A、D<<1,对等式(7)使用泰勒展开求解，并且只考虑常数项，式(7)就能简化成：

(8)

由于系统势函数是对称的，跃迁时间则满足条件：τ-=τ+，因此，PNBSR系统模型的逃逸率可以被计算得到：

(9)

再根据文献[17,19-20]可知CBSR系统的输出信噪比表达式为：

(10)

(11)

同样为了更直观清楚的描述PNBSR系统和CBSR系统输出信噪比随着噪声强度D变化的规律，在同样参数A=0.2的条件下，得到输出信噪比随着噪声强度D变化曲线如图3所示，由图可知曲线的趋势都是先增大后减小的趋势，表明有随机共振现象的发生；此外，图形上同种标记的曲线参数a=ac和b=bc，另外令l=1，则c可通过式(6)计算得到对应的数值；并且可以发现PNBSR系统的输出信噪比大于CBSR系统的输出信噪比，总的来说，PNBSR系统在轴承故障检测中的性能好于CBSR系统。

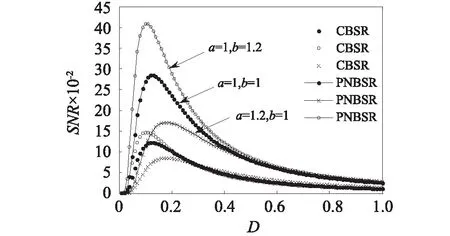
图3 不同CBSR与PNBSR系统参数下输出信噪比曲线

1.3 Levy噪声的特征函数与产生方法

为了完整起见，我们给出了Levy噪声的简单介绍，Levy噪声又称α噪声，它的产生保持了自然噪声的特性和传播机制，其非高斯分布的特性与工程应用中观测到的数据有很好的吻合,所以本文所使用的噪声为Levy噪声。

Levy噪声服从分布Lα,β(ξ,δ,μ)，其特征函数表达式为

(12)

由式(12)可知，Levy噪声的分布由α,β,σ,μ唯一确定，其中α∈(0,2]为特征指数，它决定该分布的拖尾特性和脉冲特性。α值越小，拖尾特性越弱，脉冲特性越强。反之，α值越大，拖尾特性越强，脉冲特性越弱。当α=2时，服从高斯分布；当α=1且β=0时服从柯西分布。参数β∈[-1,1]是对称参数，它与分布的对称性关系密切。β>0时分布偏左，β<0时分布偏右；参数σ∈[0,+∞)为尺度系数，与高斯分布中的方差类似；μ∈(-∞,+∞)为位置参数，表示分布的中心位置。

Levy噪声的随机变量X通过Chambers-Mallows-Stuck(CMS)方法[21]产生，当α≠1时，

(13)

式(13)中随机变量V～U(-π/2,π/2)，随机变量W～e(1)，V和W相互独立，其中

(14)

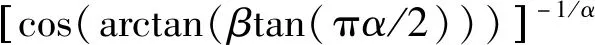
(15)

当α=1时，

(16)

除了上述的几个特殊的情况外，α稳定分布的概率密度函数没有封闭的形式，只能通过数值计算来获取近似值。

1.4 数值仿真算法

由PNBSR系统的随机变量(x,t)的Fokker-Planck方程(FPE)可知其概率密度函数[22]：

(17)

在实际工程应用中，由于s(t)多为非线性信号,因此-∂[s(t)ρ(x,t)]/∂x为非线性项，故而该方程无精确的解析表达式，需要从已有的系统选取适合的数值解析方法；由于PNBSR系统加入了Levy噪声，所以本文将算法与四阶龙格-库塔(Runge-Kutta)算法对(17)式的方程进行数值仿真求解，推导出以下算法：

(18)

式中：un表示输出信号第n次采样值；h为时间步长，一般选取h=1/fs[23]；fs为数值仿真的采样频率；ξn表示Levy噪声第n次采样值；由于Levy噪声的特征指数越小，脉冲幅值就越大，振荡粒子跳跃的距离很可能趋向无穷大，针对这个问题，本章在数值仿真时对系统输出x(n)进行截断[24]，即当|x(n)|>5时，令x(n)=sgn(x(n))×5。

2 性能指标和参数寻优

2.1 系统性能指标

在众多衡量SR系统性能指标中，主要有线性响应敏感度噪比、信噪比增益、平均能量分布等等，系统输出信噪比增益的应用最为广泛，但是由于信噪比不固定，随着输入信号变化而变化，所以本文采用更能反应SR系统，对输入信噪比(SNRin)有改善作用的平均信噪比增益作为衡量指标，平均信噪比增益定义为：

(19)

式中:MSNRI为平均信噪比增益，SNRIi第i次仿真的信噪比增益，只有当平均信噪比增益的值大于1时，才能说明随机共振系统对信号具有明显的增强和改善作用。第i次仿真的信噪比增益定义为：

(20)

式中:Sin(f0)和Sout(f0)分别表示PNBSR系统输入信号和输出信号的功率；Nin(f0)和Nout(f0)分别表示PNBSR系统输入和输出噪声功率。

2.2 自适应参数寻优算法

常用的自适应算法有多种，量子粒子群算法，人工鱼群算法，遗传算法等智能算法和遍历法等。为探索PNBSR系统参数l,c,a和b对随机共振系统性能的内在规律，本节首先采用量子粒子群算法对系统参数l,c,a和b进行寻优，它能够帮助快速找到各个参数最佳值的范围，然后利用遍历法倾向于深入观察各个参数对下性能指标的变化规律的特点，以平均信噪比增益MSNRI为衡量指标进行寻优；以参数l和c为例(a,b同)，具体步骤如下：

(1)初始化输入信号及Levy噪声各项参数，令PNBSR系统参数初始值l=0.1和c=0.1，l和c的寻优范围都为[0.1, 2]，步长都取值为0.1；

(2)将含有噪声的输入信号送入到PNBSR系统，初始化最佳信噪比增益OMSNRI=0，l=l+0.1，c=c+0.1;

(3)根据式(20)，式(21)计算MSNRI，若MSNRI≥OMSNRI，则更新OMSNRI=MSNRI，并记录此时的l和c；若l和c未达到边界值2，则跳回步骤(2)；

(4)将OMSNRI对应的一组或多组PNBSR系统参数l和c代入系统求解。

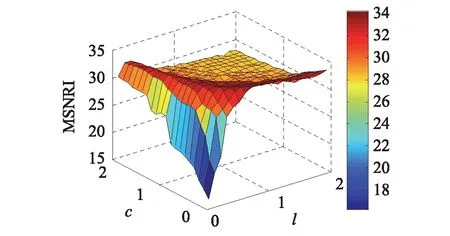
(a) MSNRI随l和c变化的三维图

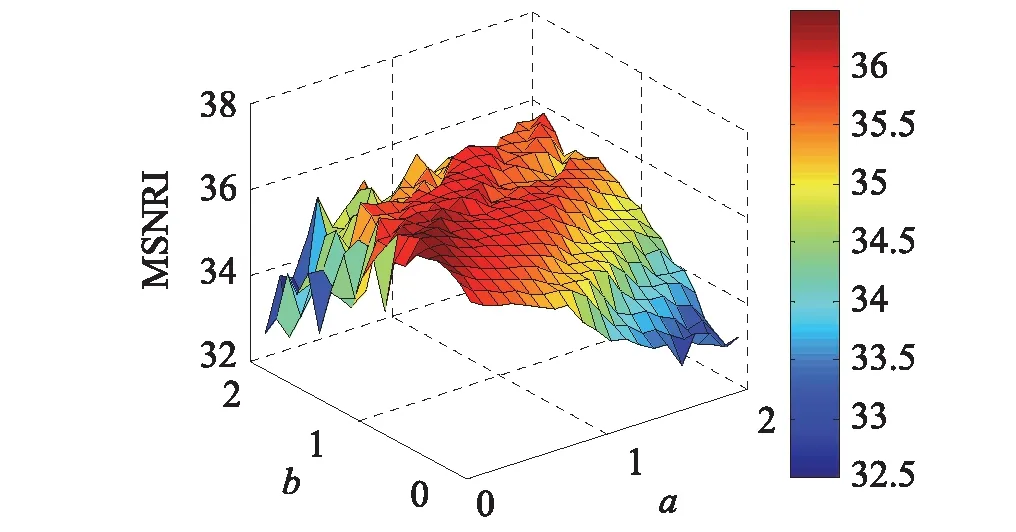
(b) MSNRI随a和b变化的三维图

实验中取幅值A=0.5，频率f=0.01 Hz；Levy噪声各项参数分别为α=1，β=0，σ=1，μ=0，D=0.3；采样频率fs=5 Hz，取样点数N=4 096；采用上述的量子粒子群算法寻优，得到仿真结果如图4所示。图4(a)是MSNRI随l和c变化的三维曲面图，可以发现存在多组系统最佳参数对l=0.4,c=0.6；l=0.5,c=0.4；l=0.7,c=0.3等，最优参数l和c呈负相关。当c(或l)的取值越大时，产生较好随机共振效果的l(或c)选择范围越小；图4(b)是MSNRI随a和b变化的三维曲面图，存在多组系统最佳参数对a=0.4,b=0.8;a=0.6,b=0.9;a=0.8,b=1.2等，可见最优参数a和b呈正相关。当a(或b)的取值越大时，产生较好随机共振效果的b(或a)选择范围越大，因此改善了传统随机系统由于参数选择不当造成随机共振效果不佳的问题。

3 Levy噪声环境下PNBSR系统弱信号检测与参数诱导随机共振现象

将混有Levy噪声的输入信号输入到PNBSR系统中，这里选取PNBSR系统幅值A=0.5，系统参数l=0.5,c=0.5,a=0.9,b=0.4，与CBSR系统做了具体的仿真对比；图5(a)表示的是含噪输入信号的时域图和功率谱图，图5(b)所示的是信号通过CBSR系统后的输出信号时域图和功率谱图，可以发现通过CBSR系统后信号能被有效的检测出来，图5(c)所示的是通过PNBSR系统后的时域输出信号图与功率谱图，与图5(b)所示的CBSR系统的输出频谱有明显的增大，频谱在f=0.01 Hz处有明显尖峰，说明此时待测弱信号的频率已被检测出来，实现了Levy噪声环境下的弱信号检测；并且由图5(b)和(c)的频谱计算出，相对于CBSR系统的信噪比增益(27.31 dB)，通过PNBSR系统后的信噪比增益(31.32 dB)有明显的增大；这是由于CBSR系统输出饱和性限制了它的增强能力，而PNBSR系统消除了这种特性，会使输出信号的幅值成倍增强，使它比CBSR系统具有在更强的强背景噪声下检测信号的能力，更适合应用在故障检测中。

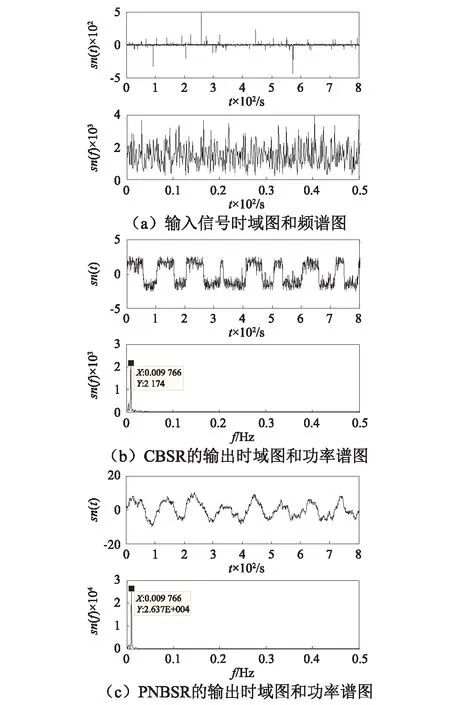
图5 输入信号与输出信号时域和频域图

下面将深入研究Levy噪声环境下，特征指数α，对称参数β取值不同时，PNBSR系统参数l,c,a和b及噪声强度系数对PNBSR系统输出的作用规律。

3.1 不同特征指数下的随机共振

3.1.1 MSNRI在不同特征指数α下随PNBSR系统参数l的变化

待测微弱信号的频率和采样频率不变，分别取Levy噪声特征指数α=0.7，α=1，α=1.3，其中β=0，σ=1，μ=0，根据前文自适应算法寻优结果选择参数，进行仿真实验；系统参数c=0.5，a=0.9，b=0.4，噪声强度保持D=0.5不变，得到不同α下平均信噪比增益MSNRI随l的演变曲线如图6(a)所示；为了更详细的分析不同α下系统参数l对随机共振输出的影响，分别研究了α>1和α<1时，MSNRI随着参数l的变化曲线如图6(b),(c)所示。

图6 不同α下MSNRI随l变换曲线

由图6(a)可知，Levy噪声环境下的PNBSR系统的MSNRI随参数l的增长，总体上呈现出先增后减的变化趋势，取值不同时产生随机共振的共振峰区间大致都是一样，且在l=0.5时达到最大值，此时非线性系统、噪声及输入信号三者达到了最佳匹配关系，即产生最佳随机共振；并且随着l的逐渐增大，会造成系统响应时间过长，使得非线性系统、噪声及输入信号三者间的最佳匹配关系逐渐消失，从而导致MSNRI逐渐下降，不足以信号在频谱中清晰地显示出来；当α>1时，通过分析图6(b)可知，α越大，MSNRI越小；当α<1时，由图6(c)可知，α越小，MSNRI越小；与图6(b)相比可知，α<1时的MSNRI整体上大于α>1时的MSNRI，从而进一步验证了Levy噪声的特征指数α越小，脉冲特性越强这一特性；在结合图6又可发现，系统随机共振效应较好的区间不随α的变化而变化，且都在α=1时，系统的MSNRI最大。

3.1.2 MSNRI在不同特征指数α下随PNBSR系统参数c的变化

待测微弱信号的频率和采样频率不变，系统参数l=0.5，a=0.9，b=0.4，D=0.5不变，同样为了直观全面地展现α>1或α<1时，是否存在与上述MSNRI同样的变化规律，也分析了α>1,α<1时MSNRI的演变曲线，得到不同α下MSNRI随参数c的演变曲线如图7所示；由图7(a)可见，MSNRI都是呈现先增大后减小的趋势，意味着存在最佳的系统参数c使更多的噪声能量转化为有用信号的能量，从而产生最佳的随机共振；再由图7(b)和(c)可知，当α>1时，α越大，MSNRI越小；当α<1时，α越小，MSNRI越大，而且α值越小，在c取值为0时突变产生的增益就越大；从整体上看，α<1时的MSNRI整体上大于α>1时的MSNRI，随着的c增大，系统随机共振效应较好的区间也不随α变化，且都在α=1时，系统的MSNRI最大。

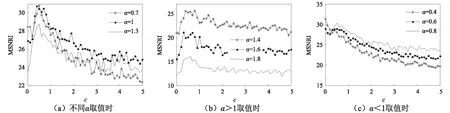
图7 不同α下MSNRI随c变换曲线

3.1.3 MSNRI在不同特征指数下随PNBSR系统参数a和b变化

待测微弱信号的频率和采样频率不变，分别取Levy噪声特征指数α=0.7，α=1，α=1,3，其中β=0，σ=1，μ=0；系统参数l=0.5，c=0.5，b=0.4，噪声强度保持D=0.5不变，得到不同α下平均信噪比增益MSNRI随a的演变曲线如图8(a)所示；从整体上看，曲线的趋势呈现先急剧减小再缓慢上升到急剧下降的特点，但是产生好的随机共振的区间不随α变化，且会出现三个峰值，第一个峰值点范围内会产生好的随机共振效果，后两个峰值点由于a的取值太大，会造成系统的双势阱很深，粒子跃迁所需要的能量大，产生的随机共振效果不佳，进而随着a的再增大，MSNRI会下降到零，这是由于系统势阱越来越深，噪声的能量不足够让有用信号发生跃迁，不会产生随机共振。同样取Levy噪声特征指数α=0.4，α=1，α=1.5，其中β=0，σ=1，μ=0；系统参数l=0.5，c=0.5，a=0.9，噪声强度D=0.5保持不变，得到不同下平均信噪比增益MSNRI随b的演变曲线如图8(b)所示；随着系统参数b的增加，MSNRI均呈现先增加再急剧减小到平稳下降的特点，且α的值对产生好的随机共振区间没有影响，整体上看，α=1时产生的MSNRI最大。

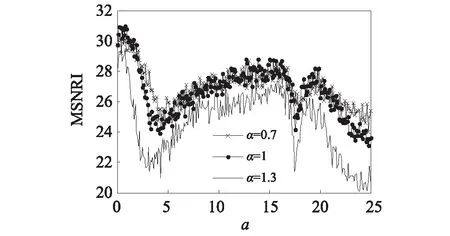
(a) 不同α下随a的变化曲线

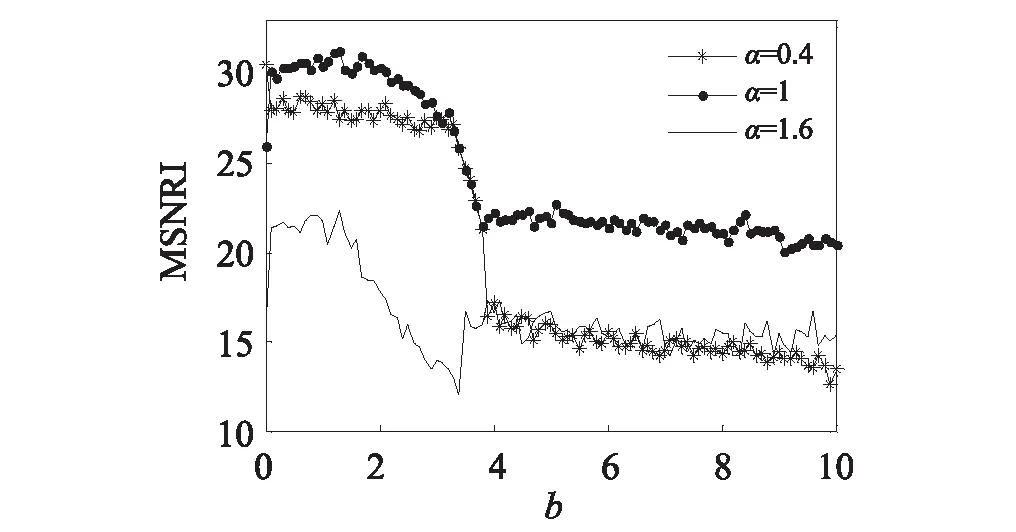
(b) 不同α下随b的变化曲线

3.1.4 在不同特征指数下随噪声强度D的变化

待测微弱信号的频率和采样频率不变，分别取Levy噪声特征指数α=0.5，α=1，α=1.5,其中β=0，σ=1,μ=0；系统参数l=0.5，c=0.5，a=0.9，b=0.4;图9为不同下MSNRI随D的演变曲线；由图可知，三条曲线走势大致相同，MSNRI均呈现随D先急剧增大后缓慢减小的趋势，可以看到α越大，产生最佳随机共振的峰值点会向右移且MSNRI会减小；再随着D增大到最佳值然后继续增大时，噪声、信号和非线性系统三者之间的协同效应逐渐被打破，使得MSNRI降低。

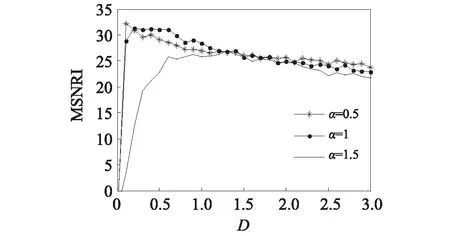
图9 不同α下MSNRI随D变化曲线

3.2 不同对称参数β下的随机共振

分别取Levy噪声对称参数β=-1，β=0，β=1，其中α=1，σ=1，μ=0，待测弱信号参数A=0.5，参数D=0.5不变；系统参数c=0.5，a=0.9，b=0.4，得到不同β下MSNRI随l的演变曲线如图10(a)所示；当β取值不同时，随着l的增大，MSNRI均呈现先增大后减小的趋势，说明存在最优的l使系统产生较好的随机共振；纵向对比可知，当β=-1和β=1时，诱导随机共振的参数区间大致一样，但共振区间向右发生偏移，且当β=0时的MSNRI明显大于β≠0时的MSNRI；系统参数l=0.5，a=0.9，b=0.4，不同下MSNRI随c的演变曲线如图 10(b)所示；由图可知，当β=-1和β=1时，两条曲线几乎重叠，但β=0时的MSNRI明显大于β≠0时的MSNRI；系统参数l=0.5，c=0.5，b=0.4，不同β下MSNRI随a的演变曲线如图10(c)所示；由图可知当β=0时随机共振区间与前文在α下的性质是一样的，但β≠0时参数a的选取对随机共振的影响不大；系统参数l=0.5，c=0.5，a=0.9，不同β下MSNRI随b的演变曲线如图10(d)所示，β=0时随机共振区间与前文α下的性质是一样的，并且β≠0时与β=0时的共振效果是一样的；系统参数l=0.5，c=0.5，a=0.9，b=0.4，不同β下MSNRI随噪声强度D变化曲线如图11所示；由图可发现MSNRI的变化规律与不同α下的MSNRI随D的变化规律相同，整体上曲线的变化是先增加后缓慢减小的趋势，且β=0时的MSNRI明显大于β≠0时的MSNRI;再次说明了噪声诱导的随机共振也能产生较好的效果。结合图10和图11可发现，β=0时系统的MSNRI大于β≠0时的MSNRI，这表明Levy噪声分布对称(即柯西分布)时，系统随机共振性能好于非对称情况。

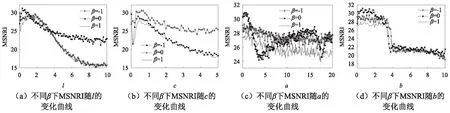
图10 不同β取值时MSNRI随系统参数的演变曲线

图11 不同β下MSNRI随噪声强度D变化曲线

4 CWRU实验验证

为验证所提的PNBSR系统在轴承检测故障中的可行性，并且选用CBSR系统对轴承故障信号的检测效果进行了对比。本文分别对内圈和外圈的深沟球轴承数据进行了分析实验，轴承故障数据来自Case Western Reserve University(CWRU)[25]的电气工程实验室，深沟球轴承型号为6205-2RS JEM SKF，其主要参数如表1所示。采样频率fs=12 kHz，采样点数N=10 000，轴承转速r=1 797 r/min。滚动轴承故障检测中可能出现的故障特征频率大都在几十到几百赫兹不满足绝热近似理论，因此采用二次采样技术进行预处理是非常必要的，其采样压缩比R=2 400。轴承的故障特征频率如表2所示，其中fs=29.93 Hz,文章仅选用滚动轴承的内圈和外圈故障信号进行分析。

(21)

表1 滚动轴承主要计算参数

表2 滚动轴承故障特征频率

式中:fr为轴承的转动频率;α为滚动体接触角;一般取值α=0。此外n、D和D与表1中的轴承参数相对应，由式(21)可以计算得到轴承外圈的故障频率fBPFO=107.3 Hz，内圈的故障频率为fBPFI=162.2 Hz。

4.1 外圈故障实例

图12(a)为轴承外圈故障信号的时域波形与频谱，故障信息不能被识别，且2 500～4 000 Hz的高频段存在大量的尖峰干扰，将大频率外圈包络信号通过二次采样后(二次采样频率fsr=5 Hz)，然后再经过上述a=1，b=1的CBSR系统后，输出信号及频谱如图12(b)所示。由图可知，频谱在f=108 Hz(在允许的误差范围内)处出现了尖峰，将故障信号送入PNBSR系统后，输出信号及频谱如图12(c)所示，可见相比CBSR系统，故障频率周围的干扰频率消除了很多，且高频段的毛刺也几乎消失，证明是外圈存在故障，验证了所提系统在弱信号检测中的有效性，且优于CBSR系统。

4.2 内圈故障实例

图13(a)为轴承内圈故障信号的时域波形与频谱，从其时域和频谱看，几乎不能识别出故障fBPFI频率=162.2 Hz，同样将大频率内圈包络信号经过二次采样后输入a=1，b=1的CBSR系统，输出信号及频谱如图13(b)所示，由图可知，频谱在f=162 Hz(在允许的误差范围内)处出现了尖峰；将内圈故障信号送入PNBSR系统后的输出信号及频谱如图13(c)所示，可见故障频率处的峰值远大于CBSR系统所检测出来的值，很容易确定是内圈存在故障，再一次证明了PNBSR系统在故障检测领域的有效性与可靠性。

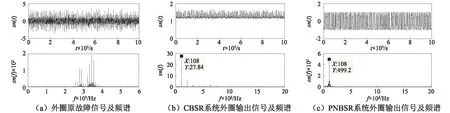
图12 外圈故障检测实例

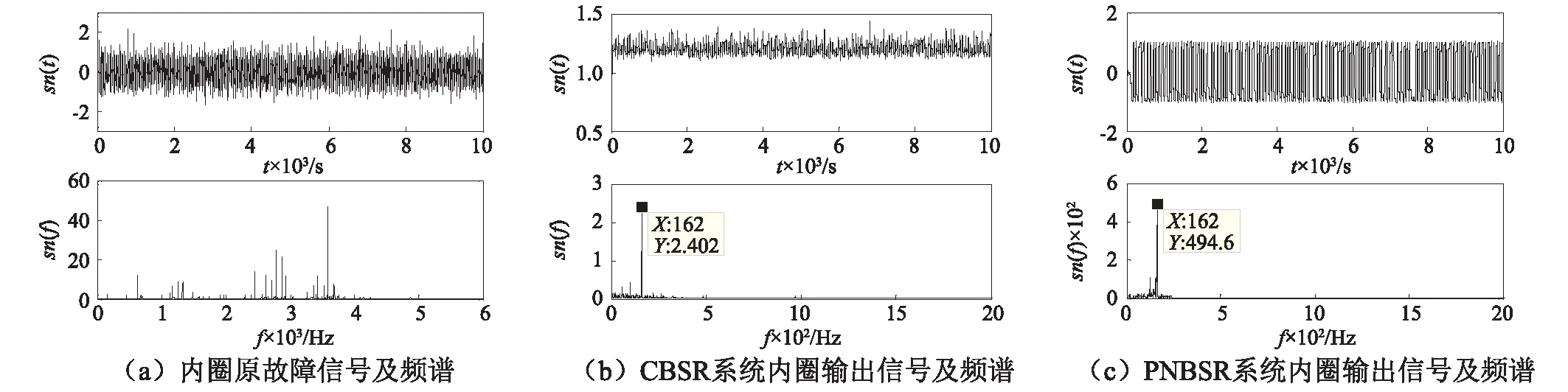
图13 内圈故障检测实例

5 结 论

本文提出了一种PNBSR系统，对系统在Levy噪声环境下的参数诱导和噪声诱导的随机共振现象进行了深入研究；研究结果表明：①相对于CBSR系统的输出信噪比，PNBSR系统的输出信噪比有4 dB的提高；②在Levy噪声分布参数α，β取不同值的条件下，改变系统参数l，c，a，、b和噪声强度放大系数D均可诱导随机共振；③在不同特征指数α下，对于一个确定的系统参数l(或c或a或b)，MSNRI整体上表现出先增大后减小的趋势，说明存在最优的系统参数使PNBSR系统、Levy噪声和输入信号产生随机共振，当α=1时，随机共振输出效果最好，且α>1时的MSNRI要小于当α<1时的MSNRI；④在不同特征指数α下，对于逐渐增大噪声强度放大系数D，α越大，产生最佳随机共振的峰值点会向右移且MSNRI会减小；⑤在不同对称参数β下，对于系统参数l,c,a,b和噪声强度放大系数D中的任意一个参数的变化，β=0时的随机共振输出效果要比当β≠0时的共振效果好；以上结论为Levy噪声环境下参数诱导的随机共振现象系统参数的合理选取提供了依据，有助于随机共振应用在工程实践中。