一维有限深势阱的转移矩阵法求解

陈凤翔 曹功辉 汪礼胜

(武汉理工大学理学院物理科学与技术系，湖北 武汉 430070)

一维势阱是量子力学中最简单最基本的模型，在量子力学教学和科研过程中起着基础性作用[1]。其理论结果在许多实际系统中也得到了很好的应用，比如在低维量子系统(如量子点、量子面、量子线等)中[2]。但作为量子力学中的基本方程，薛定谔方程[3]的求解却并不简单，在《量子力学》课程的教学过程中，除了一维无限深势阱、一维谐振子势等特殊一维情形有解析解外，一般情形很难求解。即使对于处在一维有限深势阱中的运动的粒子，当其处于束缚态时，由于确定其能级的是超越方法，无法具体给出它们的能级的解析表达式和归一化波函数[4]。

薛定谔方程的求解可分为解析法和数值法两种，解析法主要有WKB法、变分法等，数值法有打靶法[5]和有限元(FEM)法等。作为一种有益的探索，本文以处理多层光波导问题的转移矩阵(TM)法为算法，求解粒子在不同一维有限深势阱中运动的能量本征值，并利用Matlab作为计算工具，绘制出对应的波函数图像。采用TM方法计算，通过不同势阱的设置，可以得到定性的准解析规律性结论，为解释实验现象提供重要的理论依据。而且，在《量子力学》课程的学习中，学生可借助不同势阱的计算分析将理论学习进行拓展，更直观更透彻地理解一维势阱相关方面的知识点，加深对相关物理概念的理解。

1 转移矩阵法

1.1 算法应用依据

转移矩阵法起源于光学，用于计算多层薄膜介质的反射率和透射率。在光波导技术中，转移矩阵法用来建立不同介质层间的场分布联系。而经过对比发现：不含时的薛定谔方程与平板波导的波动方程在形式上是一致的；同时一维势阱模型与平板波导模型相类似，因而转移矩阵法也能够用于解决一维有限深势阱问题[6]。

平板波导的波动方程为[7]

(1)

其中k0=2π/λ，是光在真空中的传播常数，Ey为y方向的电场，β为电磁场沿z方向的传播常数，nj对应于波导中不同层的折射率，j=0,1,2。

不含时的一维薛定谔方程形式为

其中V(x)表示势能，m为粒子质量，E和ψ分别代表粒子的能量本征值和本征函数，上式经过变形，有：

(2)

对比方程(2)与方程(1)即可发现：这两个方程在形式上是一致的，方程(2)中的本征函数ψ即对应方程(1)中的电场强度Ey，因此两个方程可采用相同的方法求解。

按照波动光学理论，光波是电磁横波，光波在空间任意位置的电磁场强度及所在介质性能之间的联系都是通过Maxwell方程组和物质方程建立，电磁波在两种介质形成的界面上反射和透射时的振幅反射因数和透射因数均可以由菲涅耳公式确定。若是一个多界面的薄膜系统，则根据以下两点[8]：(1)在每一界面处运用电磁场边界条件，将同一界面两侧的场分布联系起来；(2)利用与电磁场传播相伴随的相位差，将同一膜层上下两界面内侧的场分布联系起来，可将多界面系统看作是入射介质与薄膜、基底形成的等效介质之间的界面。将以上思路应用到任何一个复杂的薄膜系统，此时系统中光反射率和透射率问题，都可以通过其等效界面对应的等效介质进行计算。等效介质的光谱特性可以采用一个特征矩阵来表示，该矩阵也称之为转移矩阵。

非对称平板波导的模型如图1所示。通常来说折射率有n1>n0>n2，导波光可被约束在导波层中进行传播。将导波光类比为势场中运动的粒子，粒子会被约束在势能较低处运动，则导波层可看作势阱中势能低的地方，衬底层和覆盖层可看作势能相对较高的地方。从这一角度看，势阱中粒子运动的模型和波导中导波光的传播模型是一致的。基于以上分析，可将转移矩阵法应用到不含时薛定谔方程的求解。而在实际应用中，例如超晶格量子阱，虽然由能隙不同的材料组成可以形成复杂的势阱，但系统的基本特征完全可以通过有限深势阱问题获得很好的理解[2]。

图1 非对称平板波导模型

1.2 建模与求解

对方程(1)的求解，首先选取两个特解E1(x)和E2(x)，使之满足E1(0)=E′2(0)=1和E′1(0)=E2(0)=0。则方程(1)的通解可设为E1(x)和E2(x)的线性叠加，即

Ey(x)=C1E1(x)+C2E2(x)

(3)

在区间(0，d)界面上，根据(3)式可给出场分布及其导数，建立0-d界面上的转移关系：

(4)

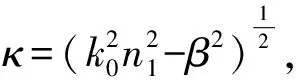
(5)

可以看出，转移矩阵仅和区间内的折射率分布、传播常数以及d有关。借助转移矩阵M，界面x= 0和x=d处的电磁场分布建立起联系。而利用矩阵逆阵的概念，可得反向传递关系，有：

(6)

由于矩阵M及其逆阵是互为逆矩阵的关系，通常两者都被称为转移矩阵。

转移矩阵法理论上可以求解任意的一维势阱，一维势阱的基本型就是一维方势阱或一维类方势阱。对于基本的一维方势阱，势能分布如图2所示。

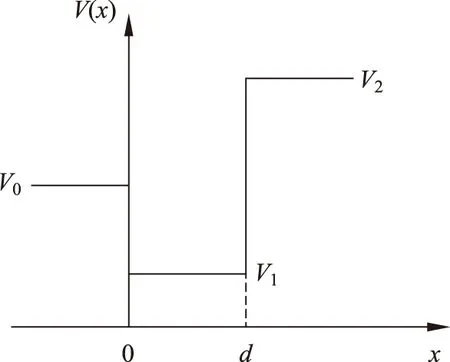
图2 一维方势阱

对应束缚态的波函数为[7]

(7)

其中

(8)

由转移矩阵理论，波函数ψ(x)及其一阶导数ψ′(x)应满足矩阵方程

(9)

根据束缚态波函数以及一维方势阱势能分布，可以得到波函数边界条件

(10)

将边界条件代入矩阵方程并进行一些简单的变换，就可得到方程

(11)

求解方程(11)即可获得粒子的能量E和相应的波函数ψ(x)。

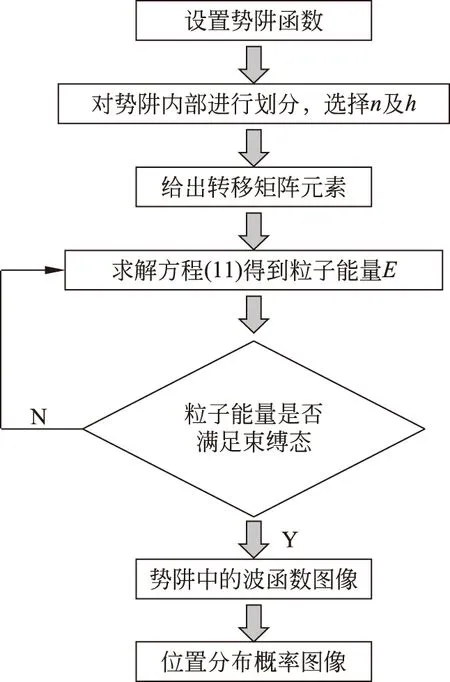
图3 一维任意势阱

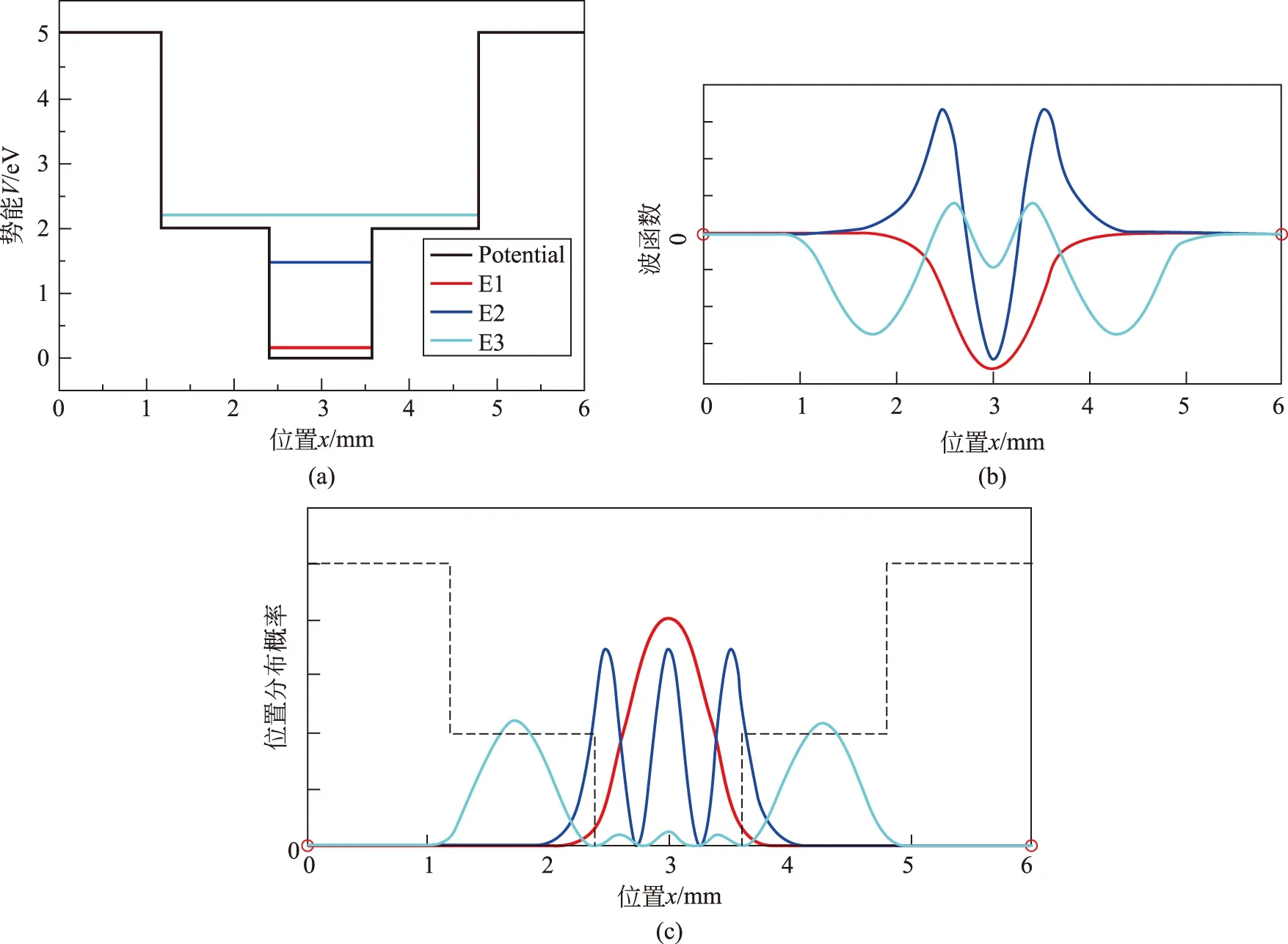
根据以上算法，可将一维方势阱推广到任意的一维任意势阱。对于一维任意势阱，其势能分布如图3所示。在x<0和x>d的区域，波函数已衰减到足够小，势场的变化带来的影响微乎其微，因此可在这两点截断，考虑x<0时，V(x)=V0，x>d时，V(x)=V2(V0，V2均为有限值)。在0

(12)

于是有

(13)

若在0E，即势场能量高于粒子能量，此时可定义

κi=iαi

(14)

利用恒等式

sin(ix)=isinh(x),cos(ix)=cosh(x)

则无需改变运算规则，同样可利用转移矩阵方法运算。可以发现计算过程中微元细分得越多，得到的能量本征值和波函数就越精确。

2 四种一维有限深势阱计算结果

图4给出了采用Matlab计算的流程图。对于不同的有限深势阱，在势阱形状参数设定后，可根据方程(11)求解粒子能量E值，如果E值满足束缚态条件，则继续运行得到势阱中的波函数和粒子的位置分布概率图示。

图4 一维有限深势阱中波函数、位置分布概率图像绘制流程图

2.1 一维对称有限深势阱

图5(a)为一维对称有限深方势阱，图中势阱为2nm宽，两边势垒高度为2eV，势阱内以不同颜色的线从低到高分别来表示n=1,2,3所对应的基态能量和激发态能量。图5(b)和图5(c)则分别给出了相对应能级的波函数和位置分布概率。在实际物理问题中，微观粒子可以被势阱所束缚，但势阱并不是无限深，而是几个电子伏的有限深势阱。从图5中结果可以看出：有限深势阱中粒子的能量仍然是离散化的；在基态情况下，微观粒子最可能的位置仍然是位于势阱正中。此结果表明，无限深势阱虽是一个理想模型，但在一定条件下，很多系统都可以抽象为无限深势阱问题来处理。但有限深势阱结果和无限深势阱结果仍略有不同。由于微观粒子并不能穿透无限深势阱，因此在无限深势阱中粒子波函数表现为在边界上截断的正弦波，而有限深势阱中，无论是处于基态还是激发态，粒子均有一定几率穿出势阱，粒子波函数延续超出势阱边界，而且随着粒子能量的增加，穿出势阱的概率逐渐增大。

2.2 一维不对称有限深势阱

在三层材料体系中，若是左右两边生长的薄层材料不一样，则为不对称有限深势阱，如常见的非对称平板波导结构。图6(a)给出了不对称有限深势阱的典型结构，为便于与图5结果对比，势阱仍设置为2nm宽，但左势垒高度降为1eV，而右势垒高度保持为2eV。图6(b)给出n=1,3,5时的粒子波函数结果，可以看出：当粒子能量较低时，如n=1,3时，此时不对称势阱对粒子的波函数并无太大影响；而当粒子能量较高，如n=5时，粒子能量高于左势垒，此时的波函数连续进入左势垒，类似波导结构中的“辐射模”。而从图6(c)来看，不对称势阱对粒子的位置分布概率也有影响，n=1基态时位置分布概率不对称情形并不明显，但随着能量的升高，如n=3时，位置分布概率的不对称性明显增加，粒子进入低势垒侧的几率增大，

图6 一维不对称有限深势阱结果演示(a) 势阱； (b) 波函数； (c) 位置分布概率

而对于n=5，粒子有更高的概率存在于低势垒中。

2.3 一维类三角势阱

超晶格量子阱物理自20世纪70年代以来得到了长足的发展，不同形式的载流子的运动规律及在外场作用下的输运问题得到较好的研究[9]。在半导体器件中，单个异质界面，如MOS结构中Si/SiO2，GaAs/AlGaAs界面附近，载流子被限制在一很窄的势阱中，通常将这类势阱称为类三角量子阱，这是在电子器件问题中最常遇到的情形[10]，同样可以采用TM理论来讨论类三角势阱中的波函数分布。

图7 一维类三角势阱结果演示(a) 势阱； (b) 波函数； (c) 位置分布概率

图7给出了一维类三角势阱的形式、波函数与位置分布概率的演示，给出的能级分别为n=1,2,3。从图7(a)来看，此时势阱中能级分布并不是均匀的，随能级升高，能级间的能量间隔逐渐减小。在图7(b)中，粒子的波函数在势阱左端全部为零，这是因为在实际的Si/SiO2界面，势垒高度可到3eV，波函数向势垒区渗入的影响完全可以忽略，效果类似无限深势阱中的“刚性壁”。而从图7(c)来看，随能级升高，粒子的分布概率呈准周期性的振荡，振荡周期越来越大，振荡幅度也越来越大，粒子很容易穿出右侧势阱而到达势阱外。对比分析类三角势阱和方势阱，可以发现：方势阱的底部水平，因此能量一定时德布罗意波长是个常数，对应波函数相邻两个节点的间距相等，这满足正弦函数的数学表征[9]；而对于类三角势阱，势阱底部从左到右上升，粒子的能量与势能之差减小，因此能量一定时德布罗意波长从左到右不断增大，波函数相邻两个节点的间距越来越大，振荡周期就越来越大。

2.4 一维有限对称双阶梯势阱

在半导体多层材料体系中，不同材料间的缓冲层设计可用来减少材料间的晶格失配，降低材料的表面、界面复合，形成的双面异质结的能带结构，则对应图8(a)中的对称双阶梯势阱，也可以将它视为一个简化的双势阱模型[11]。

图8 一维有限双阶梯势阱结果演示(a) 势阱； (b) 波函数； (c) 位置分布概率

图8(b)中给出了n=1,3,5时的波函数演示结果。从图(b)中可以看出，在对称势阱中，波函数的分布始终是对称的。当n=5时，粒子的相应能量高于较低势阱，此时波函数连续进入了中间势阱。而从图8(c)的位置分布概率来看，此时粒子有更高的概率进入在中间势阱中。

3 总结

本文将处理光导波问题的TM法成功运用到求解一维有限深势阱的不含时薛定谔方程中，得到了粒子在不同势阱内运动的能量本征值，并给出了粒子波函数和位置分布概率的图像，直观地反映出粒子在势阱内的分布情况。借助Matlab强大的计算功能，可根据实际的物理问题和物理图像，对四种不同的一维有限深势阱进行设置，直观地显示不同势阱中的计算结果，这对学生学习《量子力学》是一个很好的辅助应用，能够帮助学生更深入地理解粒子在势场内的位置分布概率、运动行为等，加深对量子知识的理解。