聚焦数量关系提升复习效率——《解决实际问题的总复习》教学实录

王 瑾

【教学内容】

苏教版六年级下册第78～80 页。

【教学过程】

一、理——联：解决实际问题的一般步骤和解决实际问题的策略

1.梳理策略。

谈话：从一年级到六年级我们遇到过很多实际问题，同时运用到一些策略，我们一起来回顾：

六年级（假设）；五年级（列举、转化）；四年级（列表、画图）；三年级（从条件想起、从问题想起）

2.梳理步骤。

提问：解决这些问题的时候，虽然运用的策略不一样，但大体上都经历了怎样的几个步骤？

根据学生的回答板书：理解题意——分析数量关系——解答问题——检验反思。

3.沟通策略与解决实际问题一般步骤的联系。

追问：这么多种策略，哪些策略更有助于我们理解题意？哪些策略更有利于我们分析数量关系？哪些策略侧重于我们解答问题？

（根据学生回答对应板书）

理解题意 画图 列表

分析数量关系 从条件想起 从问题想起

解答问题 列举 转化 假设

4.揭示课题。

谈话：不管运用什么策略，要想顺利的解决问题，都得分析数量关系！今天我们重点来研究数量关系。（板书：解决实际问题的总复习——数量关系）

二、理——联：数量关系

谈话：课前，四人小组分工合作，根据老师提供的实际问题列数量关系，甚至还自编了一些实际问题，我们按加、减、乘、除四类梳理了数量关系。

1.小组分享：根据实际问题，数量关系是怎样的？在四人小组里分享你的成果。

2.加、减、乘、除四个层次交流。

层次一：加法。

师：这位同学对加法整理的数量关系对不对？

提问：这三道题代表了用加法解决的实际问题的三种不同情况，这三个数量关系式有什么共同点呢？

生：都是用部分量和部分量相加。

提问：（指第三个问题）这种比多比少的问题也可以这样理解吗？（当堂画图展示）这种也是把两部分合起来，所以这三种可以用同一个数量关系式表示。

（板书：部分数＋部分数＝总数）

追问：这些也是把两部分合起来吗？谁来选择一个说一说？

交流总结：不管哪种加法的实际问题，它们的数量关系都可以看作是：部分数＋部分数＝总数。

层次二：减法。

师：我们先来看他们找到了哪些减法的实际问题。

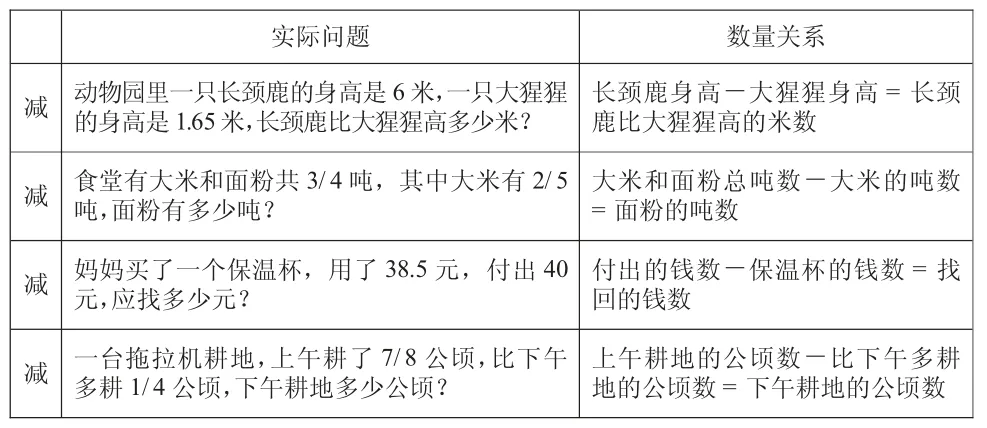
实际问题 数量关系减 动物园里一只长颈鹿的身高是6 米，一只大猩猩的身高是1.65 米，长颈鹿比大猩猩高多少米？长颈鹿身高－大猩猩身高= 长颈鹿比大猩猩高的米数减 食堂有大米和面粉共3/4 吨，其中大米有2/5吨，面粉有多少吨？大米和面粉总吨数－大米的吨数= 面粉的吨数付出的钱数－保温杯的钱数= 找回的钱数减 一台拖拉机耕地，上午耕了7/8 公顷，比下午多耕1/4 公顷，下午耕地多少公顷？减 妈妈买了一个保温杯，用了38.5 元，付出40元，应找多少元？上午耕地的公顷数－比下午多耕地的公顷数= 下午耕地的公顷数

师：他们又找到怎样的数量关系？谁来读一读？

提问：这四种减法的数量关系式，你能用一个式子表示吗？（根据回答板书：总数－部分数＝部分数）

追问：你是怎么想到的？

生：根据这位同学减法的数量关系总结出的。

追问：（指着第二个）你能用这个实际问题和数量关系来具体的说一说你想表达的意思吗？

生：大米和面粉的总吨数就是总数，大米的吨数就是部分数，面粉的吨数是另一部分数。

师：你们也能选择一个说一说吗？

师：看来，我们整理的减法数量关系可以帮我们总结，你还可以怎么想到减法的数量关系？

生：还可以根据加法来想，因为加法是部分数＋部分数＝总数，所以减法是总数－部分数＝部分数。

指出：减法是加法的逆运算，根据加法的数量关系我们很容易就能想到减法的数量关系。

总结：只要是从总数里去掉一部分求另一部分都是用减法来算。

层次三：乘法。

（1）呈现三道题：

实际问题乘 课桌椅每套325 元，华新小学买了48 套这样的课桌椅，一共要付多少元？乘 小力每分钟步行1/12 千米，15 分钟步行多少千米？乘 李师傅每小时加工24 个零件，八小时加工多少个？

（2）谈话：乘法的题有这样的三道，同样的三道题，老师发现了两种不同的数量关系式。

数量关系单价×数量＝总价速度×时间＝路程工作效率×工作时间＝工作总量数量关系每套的钱数×套数＝要付的钱数每分钟行的千米数×分钟数＝一共行的千米数每小时加工的个数×小时数＝一共加工的个数

谈话：都对吗？哪一种更简洁？（第一种）

师：跟加减法类似，这三种数量关系也能用一个式子表示吗？

生：每份数×份数＝总数。

师：老师想采访你一下，你是怎么想的？

生：我是从数量关系里看的，比如说每套的钱数，就是每份数，然后套数就是有多少份，要付的钱数就是求的总数。

师：回到前面的简洁表达的数量关系，你能说一说每份数、份数、总数分别是什么呢？

交流总结：乘法的各类实际问题都可以用这样的数量关系来表示：每份数×份数＝总数。

层次四：除法。

师：根据乘法的这个数量关系，你能联想到怎样的数量关系？

总数÷份数＝每份数；总数÷每份数＝份数。

追问：是不是这样呢？我们一起来看看。

除 何老师用810 元买了9 个足球，每个足球多少元？ 总价÷数量＝单价除 姜师傅11 小时加工1098 个零件，每小时加工多少个零件？ 工作总量÷工作时间＝工作效率总路程÷油的升数＝平均每升油能开多少公里除 张师傅加工一批零件，已加工75 个，占总数的3/4，总数有多少个？除 一辆汽车开360 公里，耗油10 升，平均每升油能开多少公里？已加工个数÷占总数的几分之几＝零件总个数

师：这几个实际问题，是属于总数÷份数＝每份数，还是总数÷每份数＝份数？

师：求单价、工作效率、单位“1”这样的实际问题都是求每份数。

交流总结：求数量，求一个数是另一个数的几倍、几分之几、百分之几都是求份数。

3.联系：这些数量关系之间相互有没有什么联系？

部分数＋部分数＝总数；总数－部分数＝部分数；

每份数×份数＝总数；

总数÷份数＝每份数；总数÷每份数＝份数。

三、练：从条件想起和从问题想起分析数量关系

1.对比练习。

2.买6 件同样的短袖衬衫要用510 元，如果用这些钱去买长袖衬衫，就要少买2 件。长袖衬衫的单价是多少元？我是从 想起分析数量关系的；1.买6 件同样的短袖衬衫要用510 元，每件长袖衬衫比短袖衬衫贵42.5 元，长袖衬衫的单价是多少元？我是从 想起分析数量关系的；数量关系式是： 数量关系式是：列式解答： 列式解答：

（1）第1 小题从条件想起。

说一说：根据_______这个条件，可以找到数量关系：_______并列出算式_______；

（2）第2 小题从问题想起。

说一说：要求出_______，要知道______，数量关系是_______，510 就是总价，4 是数量，所以可以列出算式_______。

小结：看来，有的实际问题从条件想起更方便，有的实际问题从问题想起更合适，我们需要根据不同的情况灵活选择策略帮助我们分析数量关系。

2.独立解答。

（1）出示分步计算、综合算式和简便运算三种资源；

提问：他们的计算结果都对吗？

指出：根据数据的特点灵活使用计算方法。

（2）你们都算对了吗？顺利的解决这个问题真的不难，谁能说说你是运用的什么策略分析数量关系的？

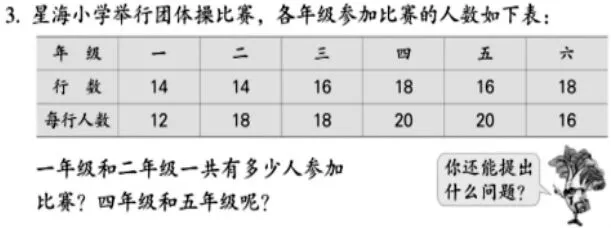
从条件想起：从表格里可以看出知道了行数和每行的人数，所以知道用行数×每行人数＝一个年级的人数，再看看问题求的是什么就可以；

从问题想起：看看问题要求的是一年级和二年级的总人数，所以再到条件中去找需要的条件就可以。

四、交流分享

通过这节课的学习，你对解决问题尤其是数量关系有了什么新的认识？对复习的方法有没有什么收获？