课内导学课外研学——《正方体的展开图》教学实践与思考

牛献礼（特级教师）

【教学内容】

人教版五年级下册《正方体的展开图》。

【教学思考】

在五年级的练习或测试中，学生经常会遇到判断一个图形是不是正方体表面的展开图的题目（如下所示）。

判断：下面几幅图中，哪几幅是正方体表面的展开图？

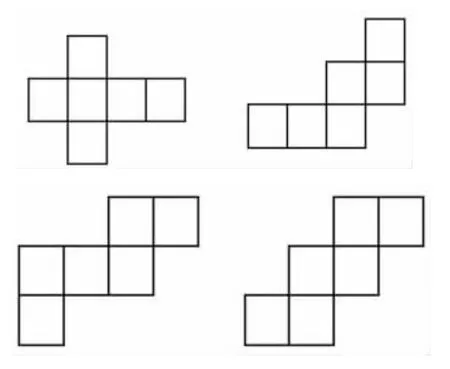
这样的判断题，学生的出错率很高。不得已，不少学生自发地“发明”了一些办法，比如把展开图描在纸上或者模仿着画出图来，再剪下来亲手折一折，用亲身实践来验证能不能围成正方体，真是费时又费力！怎么帮助学生“摆脱困境”呢？于是，笔者萌发了针对“正方体的展开图”专门上一节课的念头，期望通过对“正方体展开图”的研究，不仅让学生发现正方体和长方体的展开图的若干样式，并能进行正确地判断，更能促进学生空间观念与直观想象素养的培育。

正方体的展开图一般可以分为4 大类共11 种形状：“一四一型”“二二二型”“一三二型”“三三型”。如果只是把这11 种图式借助教师的示范操作或课件演示，让学生看懂并记下来，应对“解题”也没有大的问题。但是，这样将教学目标归于“解题”的教学，学生最终还是靠“死记”来学习知识，与“图形与几何”内容教学的核心素养——指向“空间观念的培养”相去甚远，直观想象素养和推理素养的培育得不到很好的落实。况且，这样“死记硬背”式的知识的教学，学习方式注定是被动接受式的，学生也不会喜欢，记忆也不会长久，时间一久自然也就忘却了。

那么，怎样指导学生去研究“正方体的展开图”呢？一节课短短的40 分钟时间够用吗？显然，如果给学生提供充分的“悟”的空间与时间，课堂时间是不够用的。于是，根据学生的实际情况，笔者确定了“课内导学——动手操作与推理想象相结合，重点研究一四一型展开图”与“课外研学——以探究性作业的形式呈现，重点研究正方体其他类型的展开图”的教学思路。

方向一旦明确，目标也随之清晰。

【教学过程】

●教学片断一

先让学生在课前自己准备的正方体纸盒上标出“上、下、左、右、前、后”，再按照要求沿着画有红线的棱剪开，得到正方体的展开图（如图1）。然后让学生把展开图重新折成正方体，仔细辨别展开图中的各个面分别是正方体中的哪个面。

图1

师：请大家仔细观察这个正方体的展开图，你有什么发现？

生：我发现正方体原来相对的面现在都是隔开的，比如上面和下面隔着一个后面，左面和右面也隔着一个后面。

师：想一想，相对的面可能连在一起，变成相邻的面吗？

生：不可能。

生：我发现，前、后、上、下四个面排成一列，左面和右面在两边，整个展开图正好是一个轴对称图形。

师：左、右两个面有点像你脸上的哪个部位？

生：两只耳朵。

师：想一想，这两只“耳朵”还可以长在哪里？大家想象一下。

生：两只耳朵还可以长在最上边或者最下边（如图2、图3）。

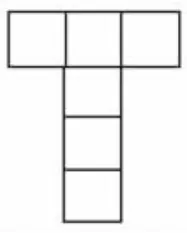
图2

图3

师：这两个图形其实是同一种，只不过摆放的方向不同。想象一下，这个图形能折成正方体吗？

生：可以，因为连排的4 个正方形可以看成前、后、上、下四个面，而两只“耳朵”正好是左面和右面。

师：如果左、右两只耳朵长得不对称（如图4），这个图形还能折成正方体吗？

图4

生：能，连排的4 个正方形可以看成前、后、上、下4 个面，而两只“耳朵”还是左面和右面。

（师生共同动手操作，进行验证）

师：像这样，两只“耳朵”不对称的展开图还有哪些情况？请画出示意图。

（学生独立画图，小组讨论交流）

出示图5：

图5

师：这个图（图5）是一个新的展开图吗？

引导学生将图5和图4进行对比，认识到图5是图4旋转而成的，实际上就是同一幅图，不能算一种新的展开图。

出示图6：

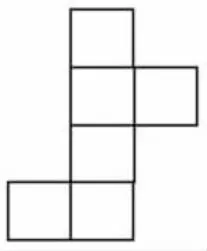
图6

师：这幅图（图6）是一种新的展开图吗？

再次引导学生将图6与图4进行对比，认识到图6是图4翻转得到的，实际就是同一幅图，也不能算一种新的展开图。

最后，学生确认还有以下3种形状（如图7、图8、图9）也能折叠成正方体。

图7

图8

图9

师：如果图形中有4 个连排的正方形，两只“耳朵”在同一边可以吗？（如图10、图11）想一想，和同学议一议。

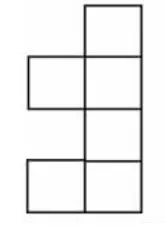
图10

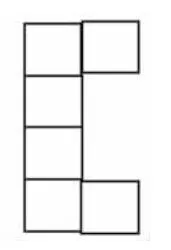
图11

生：图10不能围成正方体，因为4 个连排的正方形可以看作前、后、上、下四个面，左边的两个正方形都是左面，重叠在一起了。

生：图11也不行，它有两个右面，缺一个左面。所以不能围成正方体。

师：看来中间4 个连排的正方形的展开图只有几种呀？

生：6 种。

师：你能给这6 种展开图起个名字吗？

生：它们都是左边一排有1个正方形，中间是4 个，右边也只有1 个，可以叫作“一四一型”。

师：不知道大家想过没有，为什么“一四一型”展开图，只要中间4 个正方形不动，上面和下面的正方形不管摆在哪个位置，都能围成正方体呢？

生：“一四一型”中间是4 个正方形，正好围成一圈，这样两边的2 个正方形就像两个盖子，不管原来连在哪一个正方形上，都能盖上去。

（教师演示操作，学生直观地看到并理解了“一四一型”展开图都能围成正方体的原理）

课上到这里就要结束了，给学生留的课后作业是：正方体的展开图除了刚才发现的“一四一型”的6 种之外，还会有其他的样式吗？请你认真研究一下，并在作业纸画出每一种样式的示意图。

【思考：“正方体的展开图”主要依靠想象与推理来寻找答案。想象是在头脑里改造记忆的表象而创造新形象的过程。“想象力比知识更重要，因为知识是有限的，而想象力概括着世界上的一切，推动着进步，并且是知识进化的源泉。”爱因斯坦的这段对想象的高度评价丝毫都不过分。

但是，实事求是地讲，对于五年级的小学生而言，仅凭自己的想象来判断“正方体的展开图”比较困难，亲自动手操作一番再加以确认还是十分必要的。可以是在想象活动之前通过操作、观察，建立一个正方体（或长方体）展开图的初步表象，也可以是学生想象之后的操作验证活动。而对展开图更为丰富和深刻的理解还是要通过推理与想象来完成，也就是在推理过程中丰富对展开图的理解和认识，探寻展开图的分布规律，获得解决问题的方法与策略。如果过度依赖直观（动手操作），反而会导致学生想象能力的弱化。】

●教学片断二

第二天的数学课上，让学生来做“小老师”，借助实物投影仪向全班学生介绍自己的研究成果。

生：昨天我们研究的展开图都有4 个连排的正方形，我就想，如果只有3 个连排的正方形呢？就画出了这样的展开图：

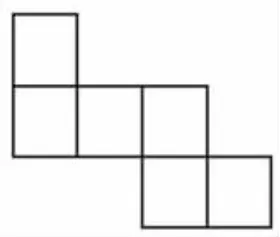
图12

然后我把它剪下来折一折，发现能够围成正方体。我就想：如果是2 个连排的正方形呢？于是就画出了第二幅图：

图13

也剪下来折一折验证了一下，发现也是能够围成正方体的。接着，我想，刚才的展开图都是分成了三行，如果分成两行可以围成正方体吗？6÷2=3（个），每行是3 个正方形，我就画出了第三幅图，验证后也是正确的。（图14）

图14

师：你很会思考！又找出了3种展开图，真了不起！其他同学还有补充吗？

生：我也是先找到了中间有3 个正方形连排的展开图（图15），然后我固定中间的3 个正方形和下面的2 个正方形，再把上面的1 个正方形向右平移一格，就得到了一个新的展开图（图16），验证后是正确的，再向右平移一格，又得到了一个新的展开图（图17），验证后也是正确的。

图15

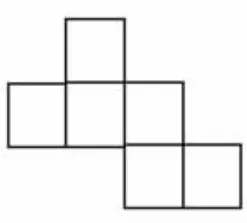
图16

图17

师：他的思考方法很有价值！通过平移上面的正方形，由一个展开图推理出了2 种新的展开图，是一个很会思考的学生！现在我们找到的中间是3 个正方形的展开图有3 种，能给这3 种展开图起个名字吗？

生：一三二型。

师：如果把图中下面的2 个正方形也向左平移一格（如图18），想一想，这个图形能折成正方体吗？

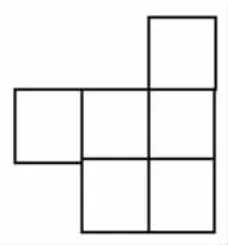
图18

学生的意见不一，教师演示折叠过程，发现图18不能围成正方体。

师：看来，图形中“田”字型的是不能围成正方体的。现在梳理一下我们的研究成果，大家一共找到了几种正方体的展开图？

生：11 种。

师：这么多种展开图，你有什么好办法能记下来，不重复、不遗漏呢？

（学生讨论后，全班交流）

生：“一四一型”一共有6 种，我先记两只“耳朵”对称的有2种，不对称的先画出一种，然后把其中一只“耳朵”不断平移，就得到了另外几种；“一三二型”也是这样，只要画出一种，再把一只“耳朵”不断平移就可以找到另外2 种了。

师：这种思考很有序，不容易重复，也不容易遗漏。

（板书：有序思考）

……

【思考：让学生在课外继续探究，完成“探究性作业”，“课已停而思未止”。课内组织学生交流“研究成果”，让学生讲述自己想象与推理的过程，讲述研究过程中的曲折与发现，创新的火花不时闪现。教师在关键处质疑、追问，澄清学生的模糊乃至错误的认识，引导学生反思经验、总结方法，学生的思维品质和自主学习能力都得到了提升。

上述案例也再次说明，设计并实施一节有价值的课，需要教师准确把握学科概念的实质与结构体系，同时了解学生学习的知识基础与心理基础。在这两方面的基础上，设计有意义、有价值、有层次的学习活动，在学生自主思考、自主活动（解决问题）的过程中适时引导、提炼以增进学生的体验与实际获得。这样的教学才能让学习真正发生，让核心素养真正落地。】