在有序操作中构建概念——《角的初步认识》教学与思考

邓晓茜

“有序思考、有序活动”是数学教学的共识。数学操作活动要以学生的学情为依据来进行组织和安排，以此积累好的活动经验，适时在有序地操作中建构概念。基于此理念，笔者对二年级上册《角的初步认识》进行了研磨，并收获了不少感悟。

【学情了解】

备课之前，笔者进行了一次小小的前测调查：首先学生看到“角”字，绝大多数的学生联想到的词语是“三角形、几角钱、牛羊角”等，小部分学生知道“锐角、钝角、直角”。其次，画出心中角的样子，绝大部分学生画的是三角形或者多边形，甚至画的是牛羊角，约四分之一学生能准确画出角的图形。由此可见，学生对平面图形情有独钟，也引起了笔者思考：何不从平面图形导入，以契合学生的认知起点。

【教学过程】

一、遮角，角自然出场

师：调皮的喜羊羊来到了我们的课堂，它还带了我们学过的平面图形。不过，都被调皮的它挡住了。你们能认出来被喜羊羊挡住的图形分别是什么吗？

（学生回答略）

师：哪个图形与众不同？师：你是怎么想的？

揭题：正是因为边是直的，所以才有角。今天我们来认识角。

【思考：从学生熟悉的平面图形入手，合乎教材编排：先认识体、再感知面、最后认识角，这样由整体到部分的顺序，契合学生数学知识的认知起点。根据裸露在外的部分来“猜”被喜羊羊“遮盖”的平面图形，吸引了学生的注意力。追问“哪个与众不同？”“你是怎么想的？”使“角”自然而然地出场。】

二、指角、描角，凸显角的本质（操作环节一）

师：（出示三角尺）你能指出它的一个角吗？（学生指顶点）

师：（显示一个顶点，然后隐去三角尺，指着点）这是角吗？

生：这是一个点。

师：哪儿才是角呢？

师：（边说边摸）从这个点出发，这两条直直的线形成的才是角。

（让学生摸一摸所带来的三角尺的一个角）

师：你能从下面的图中各找出一个角，并描出来吗？

师：（展示学生作品，并总结）我们刚才分别找到了它们当中的一个角，如果我们脱去它们漂亮的外衣，会发现：这些图形都是角，角是有大有小的，我们给它们标上记号。

【思考：这是本堂课的第一个操作环节：指角——描角——析角。层层递进，从现象到本质。指角，往往只会指角的顶点。因此，笔者放大错误，学生则会意识到还需指角的两边，这样图形的表征形式就由学生主动反思和自我调整所呈现出来了。描角，为学生提供示范的同时，也为后续的抽象提供变式图形。析角，从具体的物体中一一剥离无关信息，提炼角的要素，初步认识角的标准图形。】

三、对比辨析，使角的特征更为突出

师：这些角的形状有什么相同的地方？（同桌讨论）

生：都有一个尖尖的地方，还有直直的线。

师：尖尖的部分叫做角的“顶点”，两条直直的线叫做角的“边”。

（完成板书，并让学生指着另两幅图说出角的各部分名称）

师：仔细观察，角有几个顶点？几条边？

生：1 个顶点，2 条边。

师：下面这些图形，哪些是角，哪些不是角？

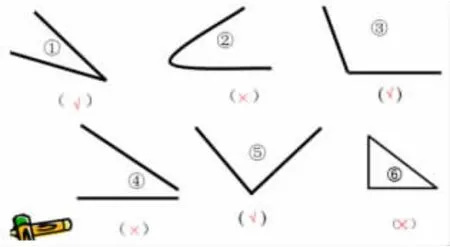
（学生说，并指明理由）

师：喜羊羊头上的角与我们今天所学的角是一回事吗？五角钱的角呢？

【思考：操作活动契合了学生的认知规律，在比较、修正、抓本质的数学活动中构建概念。所以，设计操作活动前，笔者先了解学生的认知特点：学生的前经验是什么？经验中的正迁移和负迁移分别是什么？学生对概念的理解，最困难的是什么？只有把握了学情，设计操作活动才有依据。因此，先激活数学角的前认知，再去辨析“生活角”。】

四、操作，使角的大小更可感（操作环节二）

1.角的大小与两边张开的大小有关。

（1）操作角，使角变大变小。

师：老师把我们熟悉的角请到了课堂上。有什么办法把它变得更大一些呢？

（学生操作）

师：你是怎么做到的？

生：把两条边慢慢地张开。

师：再大一些呢？

（学生操作）

师：现在我想把这个角变小一些？谁来变一变？

师：你是怎么做到的？

生：把两边慢慢地合拢。

师：再小一点。

（学生操作）

师：同学们，在操作角的过程中，我们知道了角是有大有小的（板书：角 大小），现在就让我们一起来玩玩手中的活动角。

师：请做一个比老师手中更大的角。

师：请做一个比老师手中更小的角。

师：请做一个自己喜欢的角。

（2）比角的大小。

（找三个角，投影）

师：老师找了三个角，这两个角，谁大呢？（有明显大小的）

生：用眼睛一看便知。

师：那这两个呢？（无明显大小的）

师：看不出来，我们就要比一比。把第一个角放平整，第二个角顶点对顶点，一条边对一条边地放好。如果第二个角另一条边在第一个角的里面，我们就说第二个角小，如果第二个角另一条边在外面，我们就说第二个角大。那现在就和同桌比一比手中的角吧。

（3）总结角的大小和什么有关。

师：同学们，在刚才玩活动角和比活动角的过程中，我们发现，角的两边张开的越大，角就越大；两边张开的越小，角就越小。也可以说，角的大小和两边张开的大小有关。

2.角的大小和两边的长短无关。

师：用手捏紧角的顶点，使角的大小不变。用剪刀剪短两边，角的大小变了吗？想象一下，如果把角的两边延长呢？

3.强化知识，比较大小。

师：你们现在说说，这两个角，谁大谁小？（出示红角和蓝角）那这两个呢？（教师的活动角和学生活动角比较）

【思考：先建立正确的角的大小的概念，然后再加入边的长、短这个非本质属性的干扰，都是以正确经验来修正模糊经验，如此，学生才能正确启动比较、反思、重构的模式，进而本质属性慢慢凸显，这何尝不是一种自主建构概念的数学活动经验的积累呢？教学操作最佳的排序顺序，是要反映知识的逻辑结构。第一遍磨课时，我采用先剪角，再比角的大小这样的操作步骤，发现学生无法理解什么叫“角变大变小”，因此，调整为先认识角的大小，再剪角。笔者发现“大小”这个概念的前经验会影响新知的有效建构，故只有先建立角的大小的观念，学生才能更好的理解。】