返璞归真沟通求联——复习课《运算中“1”的那点事》教学

【教学内容】

人教版六年级复习课。

【教学过程】

一、平分图形，激趣导入

师：上复习课之前，我们一起来玩一个平分图形的游戏，看看哪些同学反应最快。

师：（出示图1，小正方形的边长是大正方形的一半）有大小两个正方形，将空白部分平均分成两部分，要求大小形状相同，怎么分？

生：连接正方形的两个顶点就可以了。（出示图2）

图1

图2

师：如果平均分成三部分呢？

生：简单，都分成一样的小正方形就可以了。（出示图3）

师：如果平均分成四部分呢？

（学生思考后没有想出分法。教师出示图4）

图3

图4

师：还想玩吗？请把这个正方形平均分成七份，要求形状大小都相同。（出示图5）

（学生陷入了沉思，等了一会儿终于有学生举手）

生：很简单，只要平均分成七个小长方形就可以了。（出示图6）

图5

图6

师：做完这个分图形的游戏，你们有什么想说的？

生：做这个受到前面的影响，把图形想得太复杂，有点受误导。

师：看来最后一个图确实给大家有所启示，不需要把简单的问题想得太复杂。那在最后这幅图中能看出哪些数呢？（同桌交流）

生：如果把小长方形看成1的话，那么可以得到1、2、3、4、5、6、7 这些自然数。

师：同学们真棒，能从不同的角度去思考问题。看来“1”确实很重要，今天我们就来复习与“1”有关的问题。

【设计意图：通过分图形的这样一个情境，让学生体会到有时候思考问题需要打破思维定势，要回到问题的本质去思考解决问题，同时也激发了学生的学习兴趣。看图形说数的环节，让学生感受到从不同的角度出发看问题，往往会得到不一样的结论，也顺利引出了复习的主题，激发了进一步复习的动力。】

二、以点连线，串联成网

师：说到“1”你想到了什么？

生：1 的因数只有1，所以1既不是质数也不是合数。

生：1 是自然数的单位，比如52 中就有52 个1。

生：分数中都是将一个整体看作单位“1”。

生：1 是最小的正整数。

师：大家知道得不少，今天我们主要来复习“1”在运算中的应用。

1.简便运算中“1”的妙用。

师：同学们来看以下这些题目，你能快速说出答案吗？2×1=（ ）10×1=（ ） a×1=（ ）

师：谁来用一句话概括一下上面这几个式子？

生：任意一个数乘1 就相当于没乘，结果就等于它本身。

师：再来看这几个式子，你能快速填一填吗？2=2×（）10=10×（）a=（）×（）

师：谁又能用一句话概括出上面的几个式子呢？

生：与刚才的差不多，任意一个数都等于它本身乘1。

师：真棒！这些简单的式子我们都知道，那在我们的运算中该如何使用呢？

出示例题，学生独立完成：

2.5×36＋6.5×36＋36

师：有的同学做得快，有的同学做得慢。说说你是怎么做的？

生：我在打草稿，所以算得会比较慢一点。

生：不用打草稿，这道题可以用乘法分配律来简便计算，2.5 个36 和6.5 个36 合起来就是9 个36，最后还有1 个36，所以总共有10 个36，结果是360。

师：看来，最后的36 要看成36×1，这步很重要，这样就能进行简便计算了。

教师出示巩固练习：

（1）74×26+74＋74×73

师：做完这些题目后有什么想说的？

生：1 确实很重要，如果没有把某一项看成多少乘1 的话，有的题目就会算得很复杂，写成了多少乘1 后，计算就变得很简单。

【设计意图：就语言而言，西藏乡村小学学生的语言表达是很大的难点，学生们在数学课堂上发言胆怯，不会用语言进行表达；而简便运算也是西藏乡村小学学生学习的一项难点，运算定律背得滚瓜烂熟的背后却无法正确使用解题。在本环节先让学生从最简单的几个算式入手，根据学情锻炼学生的语言表达和概括能力，激发其学习兴趣，再转变成一道常见的简便运算题目，感受到在算式中加入1 后可以让运算简便，让学生坚定“从小入手”“撬动大问题”，激发学生学习数学的兴趣。】

2.分数计算中“1”的运用。师：同学们再来观察下面几个算式，谁能快速回答？2÷1=（ ）10÷1=（ ）a÷1=（ ）

师：谁能用一句话来概括这几个算式？

生：还是与1 有关，现在是除法，任意一个数除以1 答案等于它本身。

师：再来看以下几个算式，谁能快速回答？2=2÷（）10=10÷（）a=（）÷（）

师：谁概括一下这几个算式？

生：任意一个数都等于它本身除以1。

师：你们的语言表达越来越精确了! 那这么简单的几个算式在数学中有哪些应用呢？

师：我们都知道“整数和分数之间的加减法就是将整数化成和分数相同的同分母分数再来进行加减”，那么这道题当中的整数12，如何转化成分母是5 的分数呢？你们觉得该如何解决呢？

教师展示做法：

师：通过本题发现了“‘1’——整数和分数连接的桥梁”。

出示巩固练习：

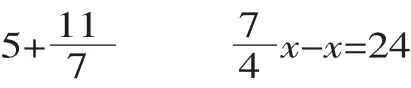
【设计意图：整数与分数相加减，相信大部分学生还是能通过以前所学进行解决，但部分西藏乡村小学学生对于整数转变成分数还是比较模糊，通过对“任意一个数除以‘1’还等于它本身”和“任意一个数都等于它本身除以‘1’”这两句话的理解，让应用变得较为熟练。】

三、拓展提升，加深理解

师：接下来有三道计算题，我们来比比谁算得又好又快。

出示题目：

120÷（120÷10+120÷15）

30÷（30÷10+30÷15）

7÷（7÷10+7÷15）

（学生独立完成）

师：大部分同学都完成了，有什么想说的吗？

生：前面两题算起来比较简单，最后一题比较麻烦，我是变成分数来计算的，这样比较方便。

生：我发现这三道题目都有除以10 和除以15，第一个数会出现三次，而且结果也是一样的，都等于6。

生：我发现虽然120、30、7 这些数在变化，但是结果不变，我刚才又换了个数，换成了60，结果还是一样的。

师：大家都非常善于发现问题，既然数的变化不影响最终结果，我们可以用哪个数来代替呢？

生：用1。

师：一起试试看。题目就变成了：1÷（1÷10+1÷15），变成分数的话就是：答案就是6。

师：这个算式是不是很熟悉？我们在哪里会经常用到的呀？

生：想起来了，在解决工程问题的时候经常用到这个算式。我们把工作总量看成了单位1。

师：课后可以与同桌一同来编一编用这个算式的应用题。这节课你有什么收获吗？

【设计意图：通过一组计算练习，让学生计算后发现其中的变与不变，数据在变、形式及结果不变，发现变化的数可以看成一个整体，用1 来表示，进一步加深了对1 的理解。同时利用算式回顾工程问题，从计算走向了解决问题，进一步建立知识间的联系。】