揭示“结构”：让解题教学更显深度

☉江苏省常熟市尚湖中学 戴晓艳

深度教学是当前一个热点教研课题，不少教师在自己的教学实践中追求深度教学.新授课中以针对教学内容的深刻理解，设计出具有深度的教学环节，促进学生深刻理解新知.但针对习题课的解题教学，如何更显深度、更有品质的题例教学研究并不多见.本文结合最近收集的几则解题教学案例，反思解题教学如何追求深度教学，供研讨.

一、解题教学讲评案例

案例1：如图1，点P是邻边为4、6的矩形ABCD内一点，连接PA、PD，作PE⊥BC于点E.分析PA+PD+PE的最小值.

图1

图2

图3

图4

讲评记录：这是一份模考试卷中的填空题，从批改情况来看，学生都不会解答，几个优秀学生误认为点P恰为矩形的中心时，PA+PD+PE取得最小值，这是一种典型错误.还有少数优秀学生有了一些进展，如图2，先确认P点应该在AD的垂直平分线上，作PH⊥AB于H点，设PE=x.PH=3，AH=4-x.由勾股定理，得AP=.设PA+PD+PE=k，则k=2+x，接下来没有进展了，于是他们放弃了这种思路.事实上，这种思路也是可以走通的，只是运算量太大，比如，整理成关于x的一元二次方程，得到3x2+（2k-32）x-k2+100=0.由根的判别式为非负数，可得关于k的不等式k2-8k-11≥0.利用二次函数的图像分析出k≥4+3，于是问题获得解决，PA+PD+PE的最小值为4+3

顺便指出，我们也可利用高中阶段的基本不等式处理.比如，设点P到AD的距离为b，则PE=4-b，可列出t=2+4-b.注意到

以上解法主要是繁杂的运算，难以顺利“算”出来，所以不少学生选择放弃了这个方向.但从上面求解来看，这是一种“通法”，是值得积累的解题经验.如果止步于这种“算”的思路，只是就题解题，满足于一种解法的获得，属于浅层次教学，我们需要追求深度教学.比如，选择构造图3进行分析，分别以AD、AP为边作两个等边三角形ADG、△APH，可证出△APD≌△AHG，PD=GH，这样分析PA+PD+PE的最小值就是过点G作GE⊥BC于点E（如图4），此时容易求出最小值就是等边三角形ADG的高3与矩形的宽4之和，即4+3.

解后回顾：进一步观察图4，当PA+PD+PE取得最小值时，点P在AD的垂直平分线上，且PA与边AD的夹角为30°.原问题中矩形的边长可以一般化为任意数据，都可使用这种几何构造的方法获得最值，这样也就可以解答以下这个经典问题.

同类链接：如图5，正方形ABCD中，对角线AC、BD交于点O.如图6，正方形ABCD中，点E、F在AD的垂直平分线上，∠EAD=∠EDA=∠FBC=∠FCB=30°，可以证明AE+DE+EF+BF+FC＜AC+BC.

图5

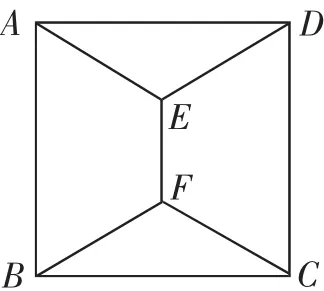
图6

案例2：如图7，梯形ABCD中，∠A=∠B=90°，AD=4，BC=6，AB=14，在边AB上找一点E，当△EAD与△EBC相似时，求AE的长.

图7

图8

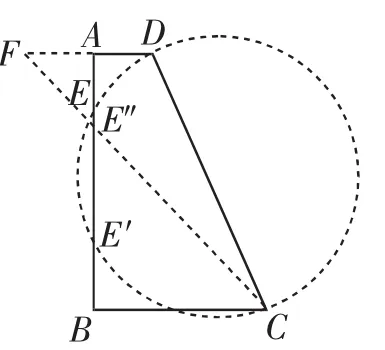
图9

讲评记录：如果我们只是满足于设AE=x，分类讨论（两种可能的相似对应）列出方程，求出x的3个值，就结束该题的讲评，则是典型的浅层次教学，入宝山而空返.我们需要进一步通过解后反思，揭示问题的图形结构.比如，先构造图8，以CD为直径作圆交AB于点E、E′，进一步根据直径所对的圆周角为直角，可得到两种相似的情形；在此基础上，如图9，取点D关于AB的对称点F，连接CF，交AB于点E″，对应着第三种情形.这样就可以让学生对这道习题的理解走向深刻，解题教学的深度也得到显现.此外，熟悉图9中构造图形的方式，还可以为一些找不到思路的学生打开思路，获得解题念头.讲评之后，再安排一道同类题跟进，巩固效果.

同类链接：如图10，在矩形ABCD中，点M、N分别在边AB、BC上，且AM=AB，将矩形沿直线MN折叠，点B恰好落在AD边上的点G处.若CD边上恰有（有且只有）2个点P，能带来△PGD与△PNC相似，探究的值.（限于篇幅，不再给出解析，答案为

图10

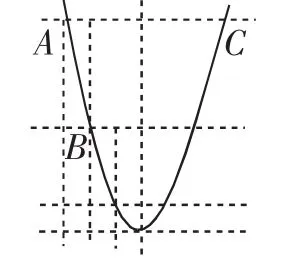
图11

案 例3：已知抛物线y=x2+bx+c经过A（m，n）、

（1）用含m的式子表示b；

（2）求n的值；

（3）求△ABC的面积.

教学记录：（1）根据A、C两点坐标的特征，容易看出抛物线的对称轴为直线x=m+3，即b=-2m-6.

（2）把点A（m，n）、C（m+6，n）的坐标分别代入抛物线的解析式，先后解出b=-2m-6，c=m2+6m+n，代入抛物线的解析式，得y=x2-（2m+6）+m2+6m+n，再把点的坐标代入，就可解出n=8.这是重要进展和关键步骤，有些学生因为这一步没有解出导致思路受阻.

（3）学生容易看出AC的长是6，且AC与x轴是平行的，但是对于AC边上的高不容易突破，因为有些学生第（2）问中的n就没能求出.事实上，如果我们深刻理解二次项系数为1的抛物线的形状，也可以直观读出AC边上的高应该是5.如图11，直观揭示了本题的深层结构，讲评时或讲评之后，有必要带领学生理解这种结构，也是加深学生对形如y=x2的二次函数图像性质的理解.

二、关于解题教学走向深度的进一步思考

1.理解习题“深层结构”，想清“多解何以归一”

教师在解题教学的讲评之前需要精心备课，不能满足于习题答案的获得，或者某一种思路的贯通，这样走进课堂，往往只是照着解答的浅层次教学，不能实现深度教学.如考题2只是满足于利用方程思想“盲解”出答案，结束讲评就“看下一道题”，就是没能走向深度教学.值得一说的是，对于有些习题，开展一题多解的教学讲评是必要的，但还需要更进一步，思考“多解何以归一”，以便帮助学生揭示问题的深层结构，使学生感受到不同解法在“高观点”反思之后的和谐与一致.

2.多让学生“讲题”展示，跟进评析并回顾反思

解题教学走向深度还需要重视发挥学生的主体作用，具体的操作要义是“让学”，即海德格尔所说的“让学生学”.在解题教学过程中，我们可以让学生走上讲台，让他们讲解对习题的理解，思路是怎样获得的，受到哪一句关键词句信息的影响，或者受到哪一种解题模型、解题经验的启示，如果没有求得最后结果，教师要通过追问让学生展示有哪些进展，主要障碍在哪一步，能否攻克某一关键步骤，等等.在讲评之后引导学生回顾反思，思考关键步骤是如何攻克的，哪些是易错点，如何纠错和究错，等等.最后，还可把同类问题进行链接式训练，帮助学生从“解一题”到“会一类”.这样，就使得解题教学走向了深度教学，也就能让学生通过“学解题”达到“会解题”.