以静制动，动静结合，合理化归，解决问题──“动圆问题”教学策略的实践与探究

☉江苏省张家港市梁丰初级中学 许凌燕

静非不动的意思，静和动只是相对而言.“动”中求“静”，“动”“静”结合，是解决几何图形中有关动点问题的常用方法.“动圆问题”作为中考的常见题型，是一个难点，题目的信息量较大，图形结构复杂，需要结合数形结合思想、空间想象和化归思想来研究图形的变化，其实数学中有关“动态”问题都有通用的解决方法：以“静”制“动”，找到“临界状态”，利用静态图形，寻找到合理的代数关系式、数量关系解决问题.基于动点问题在中考中的地位，着眼于中考命题改革的方向，根据学生对动点问题的掌握和学习情况，笔者精心准备了一节圆的专题复习课“动圆问题”，教学重点是遇到动点问题时如何以“静”制“动”，对“动圆问题”在思想方法上进行总结提炼，主要围绕探究直线（线段、射线）和圆的位置关系中的相切，揭示问题的本质，让学生在探究过程中领悟解决此类问题的一般方法.

本节“动圆问题”的专题课，整体分为三个模块，逐步递进，螺旋上升.课堂教学主要围绕学生个人展评、自主探究和小组合作交流等方式展开.

一、引例探究，初步领悟

引例是笔者自己编制的题目，难度不大，但是涵盖了直线（线段、射线）和圆的位置关系中相切的动圆问题的三类基本题型.基于学校的“自主展评式”课堂教学模式，首先布置学生回家预习引例部分.新课伊始，由三名学生依次当起“小老师”，手持教鞭，上台讲解（利用实物投影仪投影解题过程）自己的思路.

引例：如图1，∠ACB=30°，D是边AC上一点，CD=10cm.

（1）以点D为圆心、2cm为半径作⊙D，若⊙D以1cm/秒的速度沿直线AC向左运动，

①运动多少秒后，⊙D与边CB相切？

②运动多少秒后，⊙D与直线CB相切？

（2）以点D为圆心、1cm为半径作⊙D，若⊙D的半径以1cm/秒的速度扩大，问：经过多少秒后，⊙D与边CB相切？

图1

（3）以点D为圆心、1cm为半径作⊙D，若⊙D的半径以1cm/秒的速度扩大，同时⊙D以2cm/秒的速度沿直线AC向左运动，问：经过多少秒后，⊙D与边CB相切？

（1）①学生展示：

生1：将圆心D向左运动直至⊙D1和射线CB相切，假设切点为E1（如图2）.

在Rt△CD1E1中，D1E1=2，sin ∠E1CD1=，所以CD1=4，DD1=6，所以t=6s.

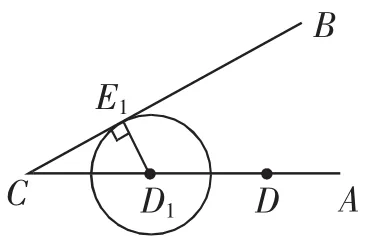
图2

图3

（1）②学生展示：

第②问是和直线CB相切，①是情况之一，情况之二是圆心D继续往左运动越过点C直至⊙D2与直线BC相切，假设切点为E2（如图3）.

在Rt△CD2E2中，D2E2=2，sin∠E2CD2=，所以CD2=4，DD2=14，所以，t=14s.

综上所述，t=6s或t=14s时，⊙D与边CB相切.

师：还有“小老师”来解决这个问题吗？

生2：我开始时第②问不会，听了他的解答，我发现点D1和D2关于C点对称，这样算起来更容易.

师：这位同学说得非常好，我们要善于利用图形的性质.

（2）学生展示：

生3：⊙D的位置不动，半径逐渐变大至与边CB相切，设切点为F（如图4）.

在Rt△CDF中，CD=10，∠ACB=30°，所以ED=CD·sin30°=5，从而t=4s.

（3）学生展示：

生4：当⊙D向左运动的过程中，假设圆心D运动至点D3时，⊙D3与边CB相切，设切点为G（如图5）.

图4

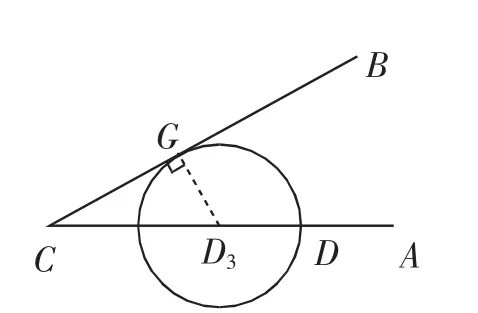
图5

在Rt△CD3G中，CD3=10-2t，D3G=1+t，∠ACB=30°，所以10-2t=2（1+t），解得t=2s.

教学设计意图：引例是将圆的动点问题放置在几何图形——角的背景下，研究动圆和射线、直线相切的位置关系，由学生讲解，将动圆的实质性问题做了剖析和归纳.圆的动态过程可以分为三类，决定元素是圆心和半径，一位置变，大小不变；二位置不变，大小变；三位置变，大小也变.解决问题的策略是：利用勾股定理、三角函数等知识点，建立方程或数量关系.辅助工具：图像，主要构造出临界位置时的静态图像，其实也是运动过程分解图.思想方法：方程思想、分类讨论思想、数形结合思想.和学生一起归纳梳理的过程中，学生发现对于相切问题，最后的静态图像都是围绕以切点和圆心为端点的线段构成的直角三角形来展开研究的，这点对于处于摸索阶段的学生很有帮助，也是“点睛”之笔.以“静”制“动”，找到“临界状态”，利用静态图形中的数量关系解决问题.

二、典题实践，自主提升

进行了引例探究教学后，进入教学实践环节，笔者选取了一道“动圆和菱形结合在一起”的中考题进行改编，原题的第（2）问为：“以P为圆心、PQ的长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点？”显然与本节课的相切主题不太契合，故做了修改：以P为圆心、PQ的长为半径作圆，在整个运动过程中，t为怎样的值时，⊙P与边BC第一次有1个公共点？同时本题采用的教学形式是学生自主探究，考查学生能否将前面总结的方法学以致用，进一步提升了学生的思维能力.

例1如图6，菱形ABCD的边长为2cm，∠DAB=60°.点P从点A出发，以cm/s的速度，沿AC向点C作匀速运动；与此同时，点Q也从点A出发，以1cm/s的速度，沿射线AB作匀速运动.当点P运动到点C时，点P、Q都停止运动.设点P运动的时间为ts.

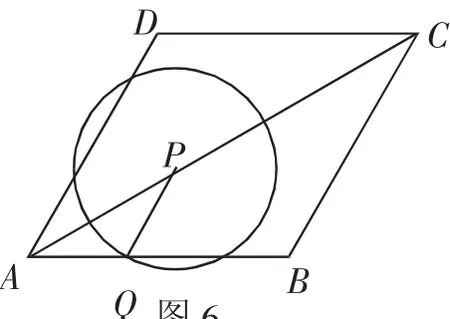
图6

（1）当点P异于点A、C时，请说明PQ∥BC；

（2）以点P为圆心、PQ的长为半径作圆，在整个运动过程中，t为怎样的值时，⊙P与边BC第一次有1个公共点？

对于此题的（1）这里不分析，学生在思考了一定时间以后，上台展示自己的探索成果，生5将图像投影出来，出现了意想不到的状况，她画的⊙P此时与边BC相切，说明她领悟到题中将“⊙P与边BC第一次有1个公共点”转为“⊙P边BC相切”，但是她呈现的图像⊙P与边AB也相切了，生6马上站起来否定了生5的结论，并阐述了他的观点：

生6：若⊙P与边AB相切，则PQ⊥AB，由第（1）问的结论知道PQ∥BC，则可以得出∠AQP=∠ABC=90°，而由菱形的性质可知∠ABC=120°，所以⊙P与边AB不相切.图像应该改为这样（如图7）.易证△APQ为等腰三角形，所以AQ=PQ=r=t，CP=2-t. 在Rt△CPR中，∠PCR=30°，所以PR=t.再利用PR=PQ，可得t=t，解得t=4-6.

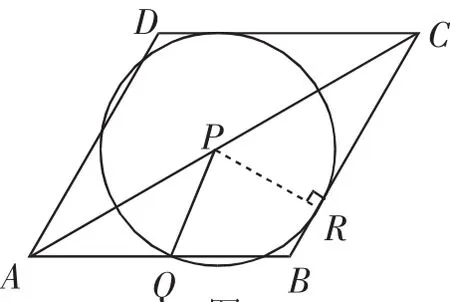
图7

教学设计意图：通过本题的研究，让学生在较为复杂的几何背景下，自主探究“动圆问题”.学生初探时只研究出⊙P与边BC相切，没有研究清楚⊙P与边AB的位置关系，这是正常现象，学生对于运动图像的整体分析和把握能力还是有欠缺的.通过此题，学生发现动态问题的辅助工具图形的重要性，而且体会到能准确、恰当、合理、简洁地画出临界的静态图像的重要性.

三、拓展延伸，活学活用

拓展延伸环节，笔者提高了题目的难度，也是采用的中考题改编题，主要考查在平面直角坐标系背景下的动圆和矩形相结合问题，题中切线也发生了变化，对学生的分类讨论、空间想象、直觉思维，提出了更高的要求，同时让学生体会利用好图形的特性，如特殊角、特殊图形、图形的特殊位置等，在解决动圆问题中的作用.

例2如图8，点A（-5，0）、B（-3，0），点C在y轴的正半轴上 ，∠CBO=45°，CD ∥AB，∠CDA=90°.点P从点Q（4，0）出发，沿x轴向左以每秒1个单位长度的速度运动，运动时间为t秒.以点P为圆心、PC的长为半径作⊙P，⊙P的大小随着点P的运动而变化.当⊙P与四边形ABCD的边（或边所在的直线）相切时，求t的值.

师：在变化的过程中，⊙P先与四边形ABCD的哪条边相切？

生：边DC（边BC）.

师：究竟是哪一条呢？边DC、边BC与⊙P都有一个公共点C，则点C就是切点，半径CP就是与切线垂直的半径，那么，你们看看在点P从点Q（4，0）出发的过程中，半径CP和谁先垂直呢？下面请六个小组分别进行讨论，给出这道题的完整答案.

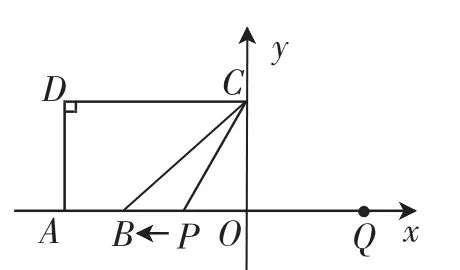
图8

……

小组1代表：我们小组研究的结果是先和边BC相切，再和边CD相切，最后与边AD相切.

①⊙P与边BC相切时（如图9），∠PCB=90°，则∠PCO=45°，OP=3，可得t=1.

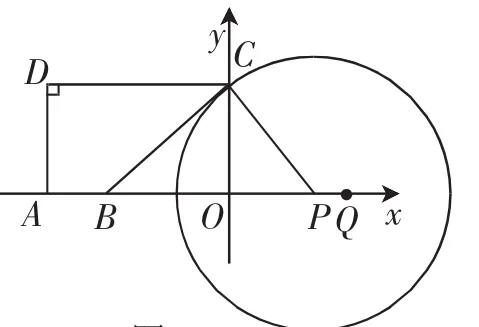
图9

图10

②⊙P与边CD相切时（如图10），PC⊥CD，P和O重合，t=4.

③⊙P与边AD相切时（如图11），AP=PC，（9-t）2=（t-4）2+32，可得t=5.6.

综上，t的值为1、4或5.6.

教学设计意图：本拓展研究题有难度，大多数学生在自主探究时会存在一定的困难，故先由教师提出问题引导学生合理探究，再采用小组合作的方式探究完成.通过本题的研究，学生的分类讨论意识更强，对于如何分类更加清楚了，学生的数学思维、逻辑推理能力和分析问题并解决问题的能力有了很大的提升.

图11

四、领悟方法，反思策略

笔者通过这节课的设计和课堂教学实践，厘清了“动圆问题”的有关教学策略.“动圆问题”作为动态几何题的一个点，表象是渗透运动变化的试题，探究其实质，揭示了“一般”和“特殊”、“运动”和“静止”的内在联系，通过课堂实践，让学生体会它们之间的相互联系和转化，知道如何让运动着的点在特殊位置或特殊时刻静止下来，达到“以不变应万变”之效.在中考中，压轴题的创新性越发显著，“动圆问题”也成为创新题型的重要对象，对学生的创新意识和创新能力提出了更高的要求.所以更需要一线教师通过教学实践，让学生经历观察、想象、推理等探究过程，善于发现动点的运动规律，以及其中包含的一些特殊图形的几何特征，化动为静，抓住临界的状态，从一般到特殊，合理作图，理性分类，解决问题.

1.以动制静，寻求突破

学生的困惑在于寻找“动”中之“静”，不能抓住“分界点”画出临界图像加以剖析.所以在“动态”问题中，引导学生寻找有价值的“静态元素”显得尤为重要.结合教师引导，学生自主探究、合作交流等不同的途径，让学生经历认知的冲突，经历想象、推理、动手实践的过程，将外在的理解转化为内在的领悟，突破自我，实现“动态”问题探究的第一个突破口——作出临界图像.

2.合理分析，用好背景

几何动态问题，必定会置于一定的特殊几何背景（特殊角、特殊四边形、图形的特殊位置关系）中，在例题的设置上，笔者从角、菱形、矩形到平面直角坐标系，引导学生善于利用好特殊几何图形的性质和位置关系，如切线和过切点的半径形成的直角三角形等，建立数量关系，从而解决问题.

3.领悟方法，感受魅力

本节课的教学过程中，笔者注重引导学生利用数形结合思想，从“形”的直观切入，到“数”的理性分析，体验了用平时所学的坐标、方程、解直角三角形及三角函数等知识服务于动圆和直线的相切问题，让学生经历了“几何问题”到“代数问题”再回归“几何问题”的转化过程，感知转化的具体应用.追悟方法，原来数形结合就是“数”和“形”双向转化，思维在两者之间相互切换，寻求突破信息，使得整个解题的过程呈螺旋式上升，增强了数学思维的转换能力.

4.适度拓展，彰显本质

通过题目适度的对比（如引例（1）中边BC和直线BC）、追问、拓展等，激发了学生的求知欲，拓宽了学生的视野，丰富了学生的认知，引导学生追寻“动圆问题”的本质，开启思维探究的旅程.只有感知、领悟了数学的本质，才能自如地运用好所学的知识点，才能把握好数学思想方法的运用，才能领会数学的魅力，促进学生学科素养的提升.

毋庸讳言，通过对“动圆问题”的探究，运用“以静制动”的教学思想，将动态的数学问题有效转化为静态问题进行处理，不失为破解动态问题的关键途径，对学生今后继续学习数学，尤其是逐步树立方程思想、分类讨论思想、数学结合思想起着良好的铺垫作用，同时为学生高中的数学学习，特别是动态几何题的学习打下了坚实基础.