研读课本教出深度,示范引领促进理解
—— 以七年级“不等式性质”教学为例
2019-07-03江苏省海安市海陵中学
☉江苏省海安市海陵中学 刘 生
不等式性质新授课教学是很多教研活动的热点课题,不少老师往往类比等式性质进行不等式性质的研究,通过一些具体数运算的举例引导学生发现不等号方向的规律,进而归纳得出不等式的性质,再进行大量的例、习题的训练,这种教学实施当然很有实效,但是与高品质的数学教学、追求数学育人的高标准还有一定的距离.笔者所在备课组经过充分研讨、集体备课生成的不等式性质课例重视由“数学现实”引入新课,并预设讲授如何从一般意义验证不等式性质,让学生感受到一种新的数学性质的生成需要经过证明才能确认,虽然减少了训练题的数量,但数学味儿更浓,教学效果也很好.下面先梳理该课的教学设计,并跟进教学立意的阐释,供研讨.
一、不等式的性质教学设计
教学环节(一) 创设情境,引出新知
情境引入:学习不等式之后,对于一些简单的不等式,如x+2>4,可以直接看出它的解集为x>2;但对于较为复杂的一元一次不等式,如,如何求其解集呢?这就需要学习不等式的性质,然后以此为依据将复杂的不等式进行变形求解.所以本课的任务就是研究不等式的性质.
教学环节(二) 归纳规律,验证性质
“实验1”:已知1<2,计算并比较:
1+3____2+3,1+6____2+6,1+2019____2+2019;
1-3____2-3,1-6____2-6,1-2019____2-2019.
规律发现:不等式两边同时加上或减去同一个数,不等号的方向不变.
“实验2”:已知1<2,计算并比较:
1×3____2×3,1×6____2×6,1×2019____2×2019;
1 ×(-3)____2 ×(-3),1 ×(-6)____2 ×(-6),1 ×(-2019)____2×(-2019).
规律发现:不等式两边同时乘上同一个正数,不等号的方向不变;不等式两边同时乘上同一个负数,不等号的方向改变.
教学组织:在学生发现规律之后,师生合作归纳出不等式的性质的文字表达,教师将其板书在黑板的主板区,先写出这些是“发现规律”,为了对这些规律进行验证,教师预设以下一些方法的讲授(可结合PPT进行).
比如,利用数轴进行验证.在数轴上由左到右取两点A、B,对应着数a、b,a<b.同时加上一个数,就是将A、B两点向相同方向平移一定的距离,仍然有a+m<b+m,an<b-n.
对于m>0,利用数轴演示am<bm时,可利用乘法的本质是加法,转化为加法进行演示说明.
对于n<0,利用数轴演示an>bn比较麻烦,可以利用相反数的意义,先在数轴上理解-a>-b,再扩大几倍理解an>bn.
还可从一般意义进行证明,借助于作差法.
不等式性质1的证法:因为a<b,所以a-b<0,所以a+m-b-m<0,即a+m-(b+m)<0,所以a+m<b+m.
不等式性质2的证法:因为a<b,所以a-b<0.又m>0,所以m(a-b)<0(依据:异号两数相乘,符号为负),所以ma-mb<0.所以ma<mb.
不等式性质3的证法:因为a<b,所以a-b<0.又n<0,所以n(a-b)>0(依据:同号两数相乘,符号为正),所以na-nb>0.所以na>nb.
说明:以上验证或证明可结合班情、学情进行链接选学,待学生理解并确认之后给出不等式性质的文字、符号表达方法,形成板书.
教学环节(三) 初步运用,步步有据
例1 设a>b,用“>”或“<”填空,并说明理由.
(1)a+3___b+3;(2)a-2019___b-2019;(3)-5a___-5b;
预设变式:设a<b,用“>”或“<”填空,并说明理由.
(1)a+1___b+1;(2)2a-2019___2b-2019;(3)3-5a___3-5b;(4)-
教学组织:安排学生先独立思考,再在小组内交流,并大组汇报.展示交流时,教师先示范口答的格式.如“例1(3),根据不等式性质3,不等式两边同时乘负5,不等式的方向改变,所以答案是-5a<-5b”.再如变式(4)的口答格式,“先由不等式性质2,不等式两边同时除以5,再由不等式性质1,不等式两边同时减去,不等式方向都不改变”.教师示范之后,对于每道小题,至少安排2~3个学生复述.一方面,可以让学生进一步熟悉不等式的性质;另一方面,可以促进学生区别等式性质与不等式性质的不同表达方式,这里并不是简单的机械重复的教学行为.
教学环节(四) 课堂小结,参与究错
小结问题1:本课所学习的不等式性质与等式性质有怎样的关系?你是如何理解的?在小组内举例交流.
小结问题2:运用不等式性质解以下几个简单的不等式:
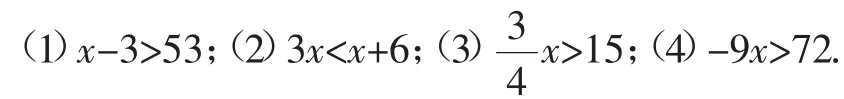
教学组织:解答展示时,需要讲出具体的方法或步骤.
小结问题3:小安提出一个命题,若x<2,则ax<2a.
请判断小安的命题是真命题还是假命题,并说明理由.
教学组织:先让学生独立思考,然后由学生评价这种解法,并进行优化改进,指出需要分类讨论,这可以促进学生对不等式性质的深刻理解.
二、教学立意的进一步阐释
(一)深入研读教材,充分想清教材导入语的用意
本课例在开课阶段的过渡语虽然简短,但是忠实于教材,是因为想清了教材导入的意图,也就是为什么要研究不等式的性质这个知识点:是因为解不等式时需要考虑的算理、依据就是不等式的性质,所以需要研究.如果我们忽略教材导入语的价值,认为它可有可无,则可能忽略它,从而采用其他新知导入方式.可见,不同的导入方法,背后往往体现了教者研究教材的深度与角度.
(二)针对班级学情,追求深度教学,发展核心素养
在上面的课例中,考虑到班级学情整体较好,我们不想在不等式性质的应用上加大题量进行机械训练,降低学生学习兴趣,让一些优秀学生处于空转状态.所以预设了带领学生一起理解不等式性质的证明.这是对教材上简单的一些数据演算、发现规律、归纳性质的必要补充,让优秀学生理解数学,懂得学习数学需要从实验发现走向一般证明.现在大家都在倡导数学育人,发展学生核心素养,我们认为,用有数学味儿的内容来促进学生理解数学,学会研究数学,用数学的套路来研究数学,正是发展学生核心素养的重要方式.
(三)重视示范引领,通过学生不断复述巩固新知
不管如何重视“以学为中心”“学生为主体”,但是“关注教”“研究教”是永不过时的,也是十分必要的,教与学的研究不可偏废.在本课例中,关于不等式性质的一般证明,需要教师的启发式讲授来节约课堂教学时间,而在应用不等式性质时,教师的示范引领作用非常关键,我们通过先示范讲解解题方法,在学生倾听理解之后,安排多名学生连续复述解题步骤,这个过程十分必要、非常有效.一方面,可以让学生对不等式性质的文字表达更加熟悉;另一方面,促进学生理解不等式变形过程中的步步有据.事实上,有了这样的过程,在不等式性质发现和归纳之后,就不需要安排学生读记、背诵的环节(相比后面讲解变形步骤,数学上使用读背的方式容易让学生厌烦),因为数学是需要理解和运用的.
