备课：先备作业——以“整式的加减（1）”为例

☉江苏省徐州市撷秀初级中学 许海英

“整式的加减（1）”是苏科版教材（六·三学制）七年级上册第三章“整式及其加减”第6节的教学内容，可以看出这是本章的核心内容，它是在前面学习了去括号、合并同类项的基础上，对所学内容的进一步深化，同时为紧随其后的解一元一次方程做好了铺垫，在教材中起着承前启后的重要作用.

一、备课

1.先备作业

传统的备课一般先备教学内容的正文部分，然后结合教师对相关内容的理解给出本节课的教学设计.这样的备课感觉针对性不强，有时会忽略教材正文部分限于篇幅而没有呈现的重要内容，于是我们建议改变传统的备课方式——备课先备作业.

作业内容主要来源于课后习题，此处课后习题共分为三个部分：第一部分是随堂练习，主要涉及简单、常规的与整式的加减有关的计算；第二部分为习题3.9，此处从知识和技能、数学理解、问题解决的角度呈现了相关题目，其中第1题和第2题的题型与随堂练习的题型一致，第3题的题型为填空题，第4题的题型与教材正文部分得到整式的加减运算法则的引例一致；第三部分为本章复习题中与此相关的题目，如第6题、第7题、第13题等，其中第6题和第7题与随堂练习的题型一致.

为便于说明，下面呈现习题3.9的第3题和复习题的第13题：

习题3.9第3题填空：

（1）（4a2+3a-2）+_____=-a2+7a+9；

（2）（3b2-4ab+6）-_____=5b2+7ab-3.

复习题第13题有一道题是一个多项式减去x2+14x-6，小明误当成了加法计算，得到的结果是2x2-x+3.正确的结果应该是什么？

2.再备教材

教材正文部分共分为四个部分：

第一部分：按照下面的步骤做一做：

（1）任意写一个两位数；

（2）交换这个两位数的十位数字和个位数字，又得到一个数；

（3）求这两个数的和.

……

解读：教材首先以文字叙述的形式呈现了一个数字游戏（记为游戏1）：交换任意一个两位数的个位数字和十位数字得到一个新数，然后将新数与原数求和（对应整式的加法运算），问：这些和有什么规律？然后以填空的形式引导学生解决这个问题.

第二部分：做一做.

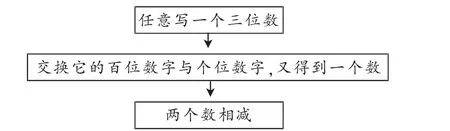
图1

解读：教材接着以程序框图的形式给出另外一个数字游戏（记为游戏2）：交换任意一个三位数的百位数字与个位数字得到一个新数，然后将新数与原数做差（对应整式的减法运算），问：这些差有什么规律？同时教材旁边以“云朵”的形式给出了任意一个三位数的表示方法，用来降低这个问题的难度.此处教材没有给出解题过程，教师应该引导学生类比游戏1的解题过程给出完整的解答.

游戏1和游戏2均以数字游戏的形式引导学生进行探索，而且呈现问题的形式多样，有利于调动学生学习的积极性和主动性.此外，上述两个数字游戏结束后，都提出了如下问题：这个规律对任意一个两（三）位数都成立吗？这样可以将学生的思维引向深处，为后续总结整式的加减运算法则做好了铺垫.

第三部分：议一议：在上面的两个问题中，分别涉及了整式的什么运算？说一说你是如何运算的.与同伴进行交流.

解读：在游戏1和游戏2的基础上，首先让学生自行归纳，然后引导学生与同伴交流，短短的一句话，既为学生指明了学习方式：自主学习和合作学习，又为学生指明了思考问题的方向，言简意赅，目的明确，起到了很好的教学效果.

第四部分：例1 计算：

（1）2x2-3x+1与-3x2+5x-7的和；

（2）-x2+3xy-y2与-x2+4xy-y2的差.

解读：例题以文字语言的形式呈现，与前述游戏1和游戏2的呈现形式的多样性一致，再次体现了教材编写的多样性，加深了学生的思维层次.其中第（1）题对应整式的加法运算，第（2）题对应整式的减法运算，两题都比较简单，将文字语言转化为符号语言后，括号前面的符号分别为+1和-1，为后续学习（整式的加减（2））较为复杂的整式的加减运算打下了坚实的基础.

二、教学设计摘录

此处只给出关于例1第（1）题的教学设计部分，第（2）题则引导学生类比第（1）题给出相应的变式.

计算：（2x2-3x+1）+（-3x2+5x-7）；

变式 1：2x2-3x+1与-3x2+5x-7的和；

变式2：若一个多项式与2x2-3x+1的差为-3x2+5x-7，求出这个多项式；

变式 3___：__-（2x2-3x+1）=-3x2+5x-7.

解读：将例1第（1）题首先还原为其符号语言作为新的第（1）题，将例1第（1）题作为变式1呈现，变式2则为其另外一种形式的文字语言，变式3为变式2的符号语言，意在引导学生进一步体会相关题目呈现形式的多样性，同时感悟它们的本质是一致的（其实就是一个题目的不同表现形式）.此外，引导学生体会文字语言和符号语言之间的转化，为后续学习做好铺垫.

布置作业：习题3.9第3题、第4题，以及复习题第13题.

解读：其他常规题目在课堂教学中已经以学生板演的形式处理完毕，引导一线教师在新兴教学媒体大量出现的今天，不要忽略传统的教学媒体——黑板.

三、学生作业情况

笔者要求学生按照以下几个部分完成作业：日期、原题、分析、正解、反思.

现将习题3.9第3题部分学生的反思摘录如下：

（1）若“_____+A=B”，则“_____=B-A”；

（2）若“_____-A=B”，则“_____=B+A”；

（3）若“A-_____=B”，则“_____=A-B”；

（4）若“A+_____=B”，则“_____=B-A”.

解读：可以看出这名学生的反思非常深刻，课后笔者和其交流得知上述四条反思是借助加减法的性质得到的，而且从他将（1）和（4）同时呈现来看，这名学生具有很好的总结和反思意识，但是其对上述四个式子未必完全理解，此处需要一线教师在学生学习了等式的基本性质和解一元一次方程中的“移项”以后，引导学生再回来看，再回来理解，相信此时必会收到事半功倍的效果.

再将另一名学生的复习题第13题的正解摘录如下：

解：由题意得___：__+（x2+14x-6）=2x2-x+3.

所以_____=（2x2-x+3）-（x2+14x-6）=x2-15x+9.

进而（x2-15x+9）-（x2+14x-6）=-29x+15.

解读：可以看出这名学生灵活地将文字语言叙述的题目转化为了用符号语言表述，而且借助例题中习得的经验将这个多项式用“_____”来代替，已经具有了很好的方程思想，此处需要一线教师告诉学生我们可以用大写的字母表示未知的多项式（如上述学生反思中用到的大写字母），为后续学习列一元一次方程解应用题打下坚实的基础.

四、结语

与本册课本对应的《教师教学用书》中给出的本节课的教学目标是：会进行整式的加减运算，并能说明其中的算理，发展有条理地思考及语言表达能力.可以看出，上述在“先备作业，再备教材”的基础上给出的教学设计与此目标是一致的，是完全吻合的.笔者也有理由相信，正是因为在备课过程中改变了传统的备课方式，先备作业，才会出现上述两名学生（不止两名）的优秀作业，欢迎更多的一线教师积极参与进来进行大胆的尝试，为此提供更多丰富的案例，贡献一份自己的力量.