数学实验工具的设计与实验教学——以“多功能套尺”的设计与实验教学为例

☉江苏省睢宁县高级中学初中部 王翠玲

☉江苏省泰州市教育局教学研究室 钱德春

数学实验是学生通过动手、动脑“做”数学的一种学习活动，它以学生为主体，以学具、实物模型或计算机等为工具，以实际操作为行为特征，以探究未知结论、验证感知结论、帮助理解结论为目的，它是一种以实验为媒介的数学思维活动.实验工具是数学实验的重要载体.笔者在教学实践中设计了数学实验工具“多功能套尺”，获得了2016年江苏省数学实验创新大赛一等奖.本文以“多功能套尺”为例，谈谈初中数学实验工具设计在数学教学中的应用，以及由此对教与学产生的价值.

一、多功能套尺的设计缘由

边与角及它们之间的关系是三角形、四边形主要学习内容.这些知识形成的途径多样，一个有效的途径是学生在教师的引导下，经历动手操作、观察、猜想、比较等过程体验、感悟、理解、掌握和内化.多年的教学实践，让笔者不禁思考：能不能制作一种实验工具，通过操作，更直观地发现和理解图形、边、角及它们之间的关系呢？笔者用学生身边唾手可得的硬纸板构思、设计了“多功能套尺”.

二、多功能套尺的结构与操作

1.多功能套尺的结构

多功能套尺将刻度尺与量角器融合为一体，是一套自带刻度的多变工具.

（1）构成：多功能套尺由一把固定标尺、一把固定角尺和若干把滑动角尺组合而成（如图1）.角尺是量角器和刻度尺的合体，量角器的零刻度线与刻度尺的刻度线重合，量角器的中心与刻度尺的零刻度重合（这是获得准确的实验数据的关键保障）；每一把角尺都可以灵活拆卸.

（2）分类：根据角尺能否滑动，角尺分为固定角尺（简称“定尺”）和滑动角尺（简称“动尺”）.

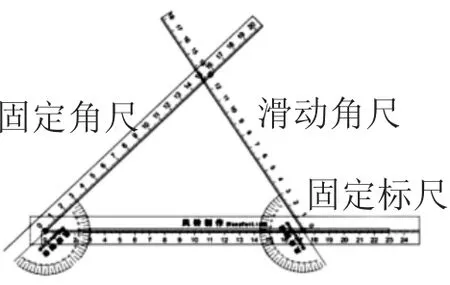
图1

2.多功能套尺的操作

滑动和旋转是多功能套尺的主要操作方式.借助多功能套尺旋转或滑动构造相应模型，探究三角形或四边形所蕴含的边或角之间的关系及全等变换、相似变换等.

在定尺的刻度线上有滑槽，动尺可以根据实验需要在滑槽内滑动，通过滑动动尺，可以改变标尺的示数，以调整图形边的大小；同时，每一把角尺都可以通过旋转，改变其与其他尺子的夹角，从而调整图形角的大小.

三、多功能套尺的功能与应用

以与三角形有关的教学为例.利用多功能套尺可以进行与一般三角形、等腰三角形、直角三角形、相似三角形或全等三角形等相关知识的实验探究.根据数学实验目的的不同，其实验可以分为三种类型：探究型、验证型和深化理解型.

1.探究未知结论

实验1：利用多功能套尺探究三角形全等的条件.

实验目的：通过实验，探究两个三角形全等所需要的条件.

实验准备：每名学生准备一副多功能套尺.

实验方式：小组合作（4个或多个学生一组）.

实验过程：首先，教师提出问题：当两个三角形具备多少组边或角相等的条件时，它们就全等呢？

经过学生讨论，确定实验问题：

（1）当两个三角形的一组边或角相等时，它们全等吗？

（2）当两个三角形的两组边或角相等时，它们全等吗？

（3）当两个三角形的三组边或角相等时，它们全等吗？

（4）当两个三角形满足什么条件时，它们全等？

步骤1：以小组为单位，学生甲随机构造一个三角形（如图2），以该三角形为“样本”.

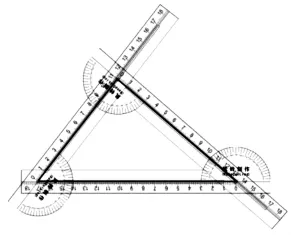
图2

步骤2：其他学生再构造一个三角形，使所构造的三角形与学生甲构造的三角形的关系分别满足以上条件，通过套尺上的标尺和量角器的示数，学生观察、比较其余的各组边、角是否确定对应相等（或利用“叠合法”），验证此时两个三角形是否能够完全重合，从而判断两个三角形是否全等（如图3）.

步骤3：归纳实验结论：

（1）当两个三角形的一组边或角相等时，它们不一定全等.

（2）当两个三角形的两边及其夹角分别相等时，两个三角形全等（简称为“边角边”或“SAS”）.

（3）当两个三角形的两边及其中一边所对的角分别相等时，两个三角形不一定全等.

（4）当两个三角形的两角及其夹边分别相等时，两个三角形全等（简称为“角边角”或“ASA”）.

（5）当两个三角形的三边别相等时，两个三角形全等（简称为“边边边”或“SSS”）.

借助多功能套尺进行探究实验，可以获得三角形全等的条件：“SAS”“ASA”“SSS”.另外，根据三角形的内角和定理，“ASA”的推论——“AAS”也是成立的，所以不需要实验探究.

对于“HL”，笔者在实验中设计以下实验过程：

（1）观察图形，提出问题：当两个三角形的两边及其中一边所对的角分别相等时，两个三角形不一定全等，那么，当两个三角形再满足什么特殊条件时它们全等？

（2）动手实验，获得结论：斜边和一条直角边分别相等的两个直角三角形全等（简称“HL”），即相当于增加“其中一组边所对的角是直角”的条件.

在探究三角形全等条件的实验中，学生以小组（至少两人）合作为主要方式，在实验中思辨、讨论、发现与归纳，获得三角形全等的条件，使“SAS”等“冰冷的美丽”变成“火热的思考”.

2.验证感知结论

实验2：利用多功能套尺验证“等边对等角，等角对等边”.

图3

实验过程：首先构造一个三角形.通过旋转图中的任意两把动尺，调整三角形角的大小.当三角形中两个内角相等时（如图4），学生根据刻度尺上的示数可以发现：相等的两个内角所对的边也相等.当然，学生通过旋转标尺或滑动量角器，可以调整三角形各边的大小.在三角形的两条边相等的条件下，观察量角器的示数可以发现：在三角形中，相等的两条边所对的角也相等.

另外，通过旋转标尺或滑动量角器调整三角形各边或角的大小，也可以验证等边三角形的性质和判定.

类似地，我们可以利用多功能套尺验证“大角对大边，大边对大角”.

该实验可以分“两步走”.

第一步：每一名学生任意构造一个三角形，通过旋尺和量角器的示数获得三角形各边、各角的度数.

第二步：学生在明确“对边”“对角”的前提下，比较每一个角所对的边的大小关系，可以发现：在三角形中，较大的角所对的边较大，较小的角所对的边较小；反之亦成立.

不同的学生往往构造不同的三角形，教师鼓励同学之间相互交流，从而获得更为充分的三角形实例，为探究实验提供更为丰富的实验资源.

实验3：探究“由平行线得相似”.

在三角形套尺的基础上，再安装一把动尺.下面，通过两种操作方式进行探究实验，以探究相似三角形的判定定理：平行于三角形一边的直线与三角形的另外两边相交，所构成的三角形与原三角形相似.

图4

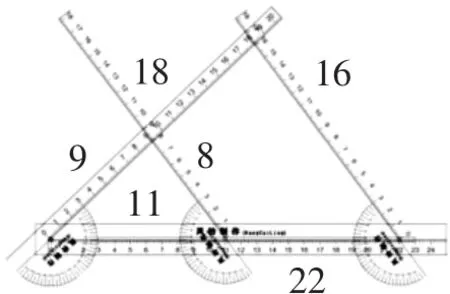
图5

方式一：“旋转”.首先旋转标尺，调整量角器的示数，根据“同位角相等，两直线平行”，使其中两把标尺平行.学生根据标尺的示数可以获得图中的两个三角形各边的长度，如图5所示，小三角形的各边分别为8cm、9cm、11cm，大三角形的各边分别为16cm、18cm、22cm，通过计算可以发现8∶16=9∶18=11∶22=1∶2，即这两个三角形的各边对应成比例，从而初步验证“平行于三角形一边的直线与三角形的两边相交，所构成的三角形与原三角形相似.”

方式二：“滑动”.在保持两条标尺平行的条件下，滑动角尺改变图中两个三角形各边的长度，通过计算得到两个三角形的各边对应成比例，加深学生对“由平行线得相似”的理解.

类似地，根据相似三角形的不同判定条件，学生通过小组合作，借助一般的三角形套尺，可以构造不同的相似三角形模型（如图6），从而为对应实验提供充分的数据，加深学生对“三角形相似的条件”的理解.

图6

3.深化理解结论

实验4：理解锐角三角函数的意义与“增减性”.

首先构造直角三角形.通过旋转角尺，调整量角器的示数，设置直角三角形中锐角的大小.根据标尺交点的示数能直接获知直角三角形各边的长度，学生根据锐角三角函数的概念可以求出对应的锐角三角函数值.

如图7左图，该直角三角形的一个锐角为30°，此锐角所对的直角边为7cm，斜边为14cm，则sin30°=7∶14=.

在保持30°角不变的情况下，滑动角尺，改变30°的角所在的直角三角形各边的大小，如图7右图，此时，该锐角所对的直角边为9cm，斜边为18cm，则sin30°=9∶18=1∶2.也就是说，30°角所对的直角边与斜边的比值不变，即30°角的正弦值总等于.类似地，我们可以验证其对应的其他锐角三角函数值也分别不变.通过以上实验，我们可以获得结论：当一个锐角的大小确定时，其对应的锐角三角函数值也随之确定.

图7

同时，通过直角三角形套尺（如图8），学生能充分感知：当一个锐角的大小改变时，其对应的锐角三角函数值随之改变，从而使学生深刻理解锐角三角函数的意义.

图8

通过“旋”“滑”“看”“算”，手、眼、脑并用，把操作实验与探究计算相结合，不仅可以对与三角形相关的一些数学结论进行探究与验证，还可以对四边形等多边形的数学结论进行探究与验证，如验证四边形的不稳定性（如图9）、探究平行四边形及特殊平行四边形的性质与判定（如图10）、任意正多边形的性质与判定（如图11）等，从而深化学生对相应知识的理解.

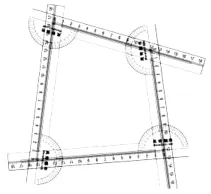
图9

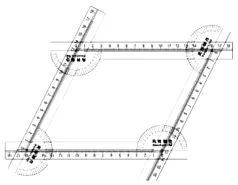
图10

图11

四、数学实验工具设计与运用对教与学的影响

作为学校数学教研组的一项研究项目，从最初的“硬纸板套尺”到目前的多种透明塑料套尺，伴随着“多功能套尺”不断改进、优化与完善的过程，学校的数学教师与数学教学发生了可喜的变化.数学教师开发与应用工具进行实验教学的热情得到激发，教学理念发生了新的变化，教学方式产生了根本性的变革；学生的学习方式得到了优化、数学学习兴趣得到了激发，数学思维能力也得到了显著的提升.

1.激发了教师实验教学的热情

多功能套尺的成功设计与教学的有效应用，带动了学校数学教研组教师数学实验教学的热情，也激发了他们的工具设计与开发的灵感.有的教师制作了木质套尺教具，有的教师制作了其他创新型实验工具，其中，“多变的四边形尺”在2018年江苏数学实验创新设计大赛中获得一等奖.

2.更新了教师的数学教学理念

皮亚杰的发生认识论认为，认识的心理发生既不是来自先天的遗传，也不是来自后天的环境，而是来自主体的行动.数学实验强调在探究活动中，学生主动参与、自主探究，亲身经历规则、基本事实及推论等的形成过程，强化“做中学”的意识，真正体现了学生的主体地位.

3.变革了教师的数学教学行为

以实验工具为支撑的数学教学，变传统的教师“知识讲授”“演示实验”为学生“自主操作”.学生借助工具动手操作、动脑思考，自主探索数学知识，拥有了创新的机会，体验了数学探究、发现知识的乐趣.

如“实验2”中，学生通过开放性实验，借助多功能套尺，不仅可以验证“等边对等角，等角对等边”，还能获得等边三角形的三个角都是60°等结论.

4.优化了学生的数学学习方式

数学实验强调“做”数学的过程，核心思想是以工具为载体，学生手脑并用，内外互动，让学生亲身经历，以带给学生深刻的学习体验和成果.可以说，数学实验工具恰恰提供了支撑数学学习方式变革的载体，它变结果性知识为过程性知识，变接受性学习为探究性学习.借助多功能套尺等工具进行数学实验，可以有效地优化学生数学学习的方式.

以“实验1”为例.在传统教学中，学生由于没有经历“三角形全等的条件”的探究过程，只知其然而不知其所以然，往往死记硬背结论.还有的学生因为缺少实验工具，一般需要利用直尺、圆规，甚至刻度尺、量角器等多种工具画图，然后度量、比较，而且由于工具的限制，难以运用“叠合法”，在验证满足一定条件的两个三角形是否全等时，常常只能通过具体的边、角的大小来确定，实验效果不明显.学生借助多功能套尺进行实验，可以直观、高效地探究两个三角形全等的条件.

5.提升了学生的数学思维能力

数学实验是一种将操作、观察、顿悟等融为一体的数学思维活动.学生在教师指导下，经历操作、观察、猜想、发现、验证等数学学习的全过程，有效促进了数学理解，发展了数学思维.

如在“探究平行四边形及特殊平行四边形的性质与判定”教学中，学生借助多功能套尺进行“四边形→平行四边形→矩形（或菱形）→正方形”的操作实验，较好地理解条件之间的关联性和图形之间的从属性，增强了数学思维的缜密性.

五、结语

数学实验工具的设计与开发，促进了教师的专业发展、教学水平的提高；数学实验工具在教学中的应用，为学生通过动手、动脑“做”数学提供了可能，引领学生真正经历数学学习的全过程，增强了学生的手脑协调及思维能力.

需要说明的是：数学实验是一种“做”数学的活动，而“做”数学具有形象、直观、感性的特点，“证”数学则具有抽象、严谨、逻辑的特点，数学教学只有将实验的“做”数学与推理的“证”数学有机结合，才能使二者优势互补、相得益彰，真正实现将“脖子以上的学习”发展为全身心融合的学习［1］.