准无衍射Lommel-Gauss光束非傍轴传输的解析*

董永胜， 胡文弢， 金洪震， 钱义先， 任志君

(1.集宁师范学院 凝聚态物理研究所,内蒙古 乌兰察布 012000;2.集宁师范学院 高速信号处理与物联网应用重点实验室 内蒙古 乌兰察布 012000;3.浙江省光信息检测与显示技术研究重点实验室 浙江 金华 321004)

0 引 言

1987年，具有实用价值的无衍射Bessel光束被首次提出并由实验产生[1].经典的Bessel光束均具有中心对称的同心圆结构.2014年，Kovalev等[2]引入了一种非对称的Bessel光束，其横向强度分布形状为新月形.最近，该团队基于不同阶Bessel函数的叠加，理论上又引入了一类新形态的无衍射光束——Lommel光束.这种光束因其在数学上可通过含有2个参量的高阶Lommel函数描述而得名[3].事实上，Lommel光束是波矢量相同的一簇Bessel光束的线性叠加.Lommel光束的独特之处在于：光束的横向强度分布对笛卡尔坐标轴具有反射对称性，特别是通过光束参数的简单调整，可以连续调节光束截面的光强分布，这是Bessel光束所没有的光学特性.Lommel光束的另一个优势在于它们的轨道角动量是连续变化的，而Bessel光束的轨道角动量则是离散变化的.不同于经典的Bessel光束，Lommel光束这些独有的光学特性将在光与物质相互作用或微操纵等领域发挥新的作用.因此，研究Lommel光束的光学特性和传输特性具有重要的科学价值.与Bessel函数类似，Lommel函数平方不可积，即理想的无衍射Lommel光束要求具有无限扩展和无限能量的特点，这在物理上是不可实现的[4].与实际存在的准无衍射Bessel-Gauss光束传输特性类似[5]，本文主要针对Lommel-Gauss光束的传输特性展开研究.

光束的传输问题本质是光束的衍射问题,而衍射问题是光学中遇到的最困难问题之一.在衍射理论中，由于数学上的困难,严格解是很少的,大多数情况下必须采用近似的方法.鉴于此，过去研究者通过构建虚光源点(“虚源法”)[5-10]研究了几种具有重要应用价值的准无衍射光束的传输特性，比如Bessel-Gauss光束[5]、cosh-Gaussian光束[6]、Mathieu-Gauss光束[7]、elegant Laguerre-Gaussian光束[8]、Hermite-Gauss光束[9]、Laguerre-Gauss光束[10]等.显然，虚源法为精确研究光束的传输特性提供了思路.本文通过虚源法，并利用光束传播的独立性和叠加性原理，将源点放入复空间，用无穷项虚光源点叠加的方式与展开的Lommel-Gauss光束一一对应.在此基础上，利用Fourier-Bessel变换和Weber积分公式推导，得到了任意阶Lommel-Gauss光束的非傍轴严格积分表达式.进一步利用该表达式解析得到了该光束轴上光场分布的解析表达式.该结果为把Lommel-Gauss光束更好地应用于实际的科学研究奠定理论基础.

1 理 论

Lommel光束[2-3,11-12]在圆柱坐标系下用一系列的Bessel函数表述为

(1)

式(1)中：ρ是径向坐标;φ为角坐标;k(传输因子)=2π/λ是波长为λ的单色光的波数；β是光束的径向参数；c是无量纲非对称参数；n是定义轨道角动量(OAM)的整型参量，代表n阶第一类Lommel函数.

根据光束传播的独立性和叠加性原理，在圆柱坐标系下，Lommel-Gauss光束能够展开为不同阶数Bessel光束的无穷项求和的形式.在z=0的平面上，Lommel-Gauss光束可用如下形式表示[13]：

(2)

(3)

式(3)中，ω0为z=0平面上光束的束腰宽度.

为研究Lommel-Gauss光束的传输，现计算z>0的场分布.根据虚源法，假设En,2p(ρ,φ,z)是由一系列位于z=zex处，半径为ρ=ρex，虚源强度为Sex(n+2p)，并有一个方位角变量的电环[4-10]所产生的，因而具体参数值取决于光束参数.设虚光源的单色标量波函数具有如下一般形式:

En,2p(ρ,φ,z)=Un,2p(ρ,z)exp[i(n+2p)φ].

(4)

光场满足非齐次亥姆霍兹方程

(5)

利用极坐标系下的Fourier-Bessel变换[6]可得:

(6)

(7)

由式(5)～式(7)联立可得

(8)

考虑到积分式(8)的复杂性，先对其进行近似处理.当式(8)满足η2≪k2时，可以将其作关于小量的级数展开.对展开式保留其首项k作为振幅因子，保留其前2项作为相位因子.式(8)化简为

(9)

由式(3)可知，ρ变化的尺度为ω0，η的变化范围为1/ω0的数量级.如果光束的束腰宽度远大于波长，那么，对于大多数光束而言，η2≪k2.而光束的束腰宽度远大于波长这个条件，除了极端情况大部分时候很容易满足.

根据Weber积分公式[13-14]

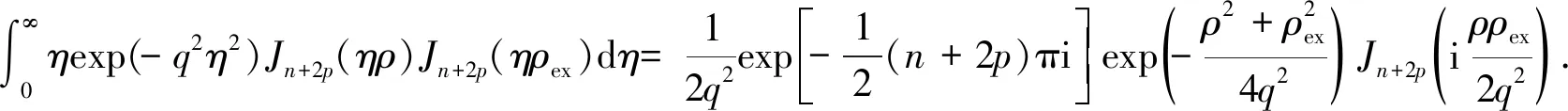
(10)

将式(10)代入式(9)计算得到

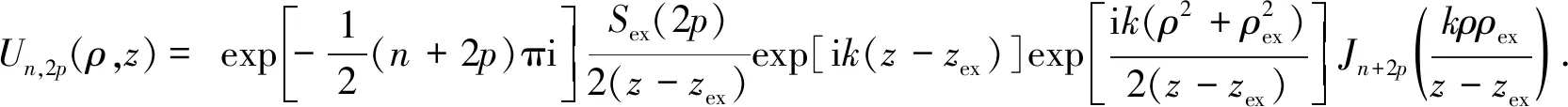
(11)

当z=0时,

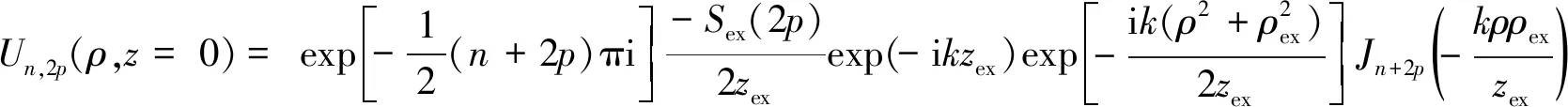
(12)

当n取偶数时，Jn+2p(x)是偶函数，故

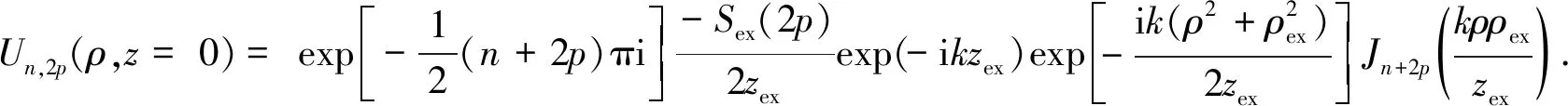
(13)

通过比较式(3)和式(13)可以得到如下参数值：

(14)

(15)

(16)

(17)

式(17)中的下标P表示傍轴近似.所以，Lommel-Gauss光束传输的傍轴近似解为

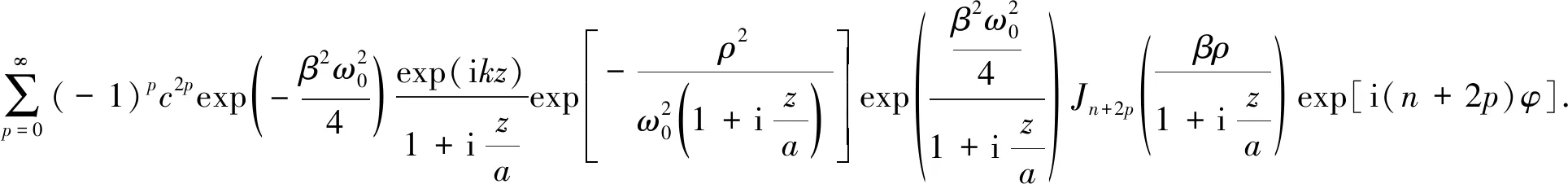
(18)

进一步将式(14)～式(16)代入式(8)，得到关于Un,2p(ρ,z)的严格积分表达式

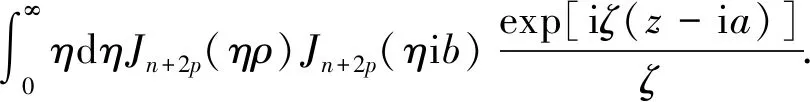
(19)

运用格林函数法进一步研究Lommel-Gauss光束传输的解析表达式.格林函数的微分方程为

(20)

式(20)中：

(21)

(22)

式(20)等号两边同时乘以exp[i(n+2p)φex]，并对变量φex积分，积分区间为[0,2π]，得到

(23)

结合式(14)～式(16)，并将式(23)和式(5)进行比较，可得到Lommel-Gauss光束的精确解析表达式

(24)

式(24)中,

(25)

Lommel-Gauss光束的傍轴近似解式(18)和严格解析积分表达式(24)是本文推导所得的第一个重要结论.

2 计 算

根据式(4)和式(19)，以n阶Lommel-Gauss光束为例，现计算轴上(z=0)光场，可以得到轴上光场的分布为

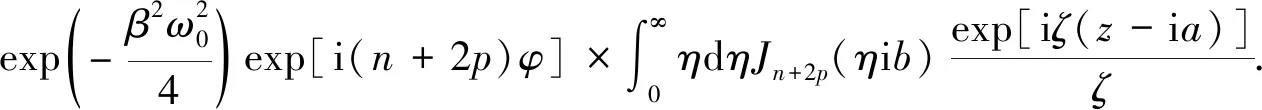
(26)

式(26)即为推导所得的Lommel-Gauss光束传输的非傍轴严格积分表达式.该解与倏逝波一样，除了包括傍轴近似解之外，还包括非傍轴场分布.

研究光束传输的轴上光场分布有重要价值[7,9-10,15]，因为很多时候人们将各类光束用于科学研究时主要关注的是光束轴上的光场分布.与过去研究Mathieu-Gauss光束[7]、Hermite-Gauss光束[9]、Laguerre-Gauss光束[10]等传输特性的方法一致，本文主要研究Lommel-Gauss光束传输过程中的轴上光场分布解析解.

对式(26)中的振幅因子和相位因子作级数展开.对于η2≪k2的情况，二者级数展开结果中只有(kω0)-2m(m=0,1,2,…,∞)及之前的项被保留，因而获得m阶非傍轴修正项[5-10].为了获得轴上光场的二阶非傍轴修正，此时m=2，即保留m=2及之前的项.在这样的展开结果下，式(26)变形为

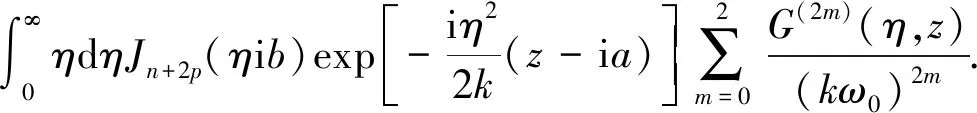
(27)

式(27)中：

(28)

G(0)(η,z)=1;

(29)

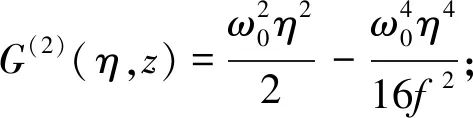
(30)

(31)

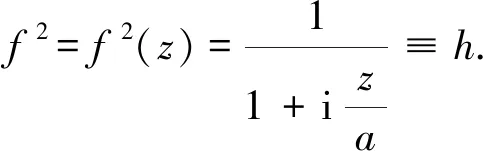
(32)

根据Weber积分公式[13-14]

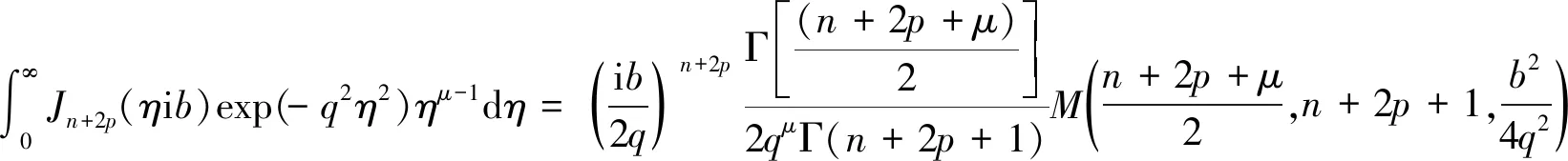
(33)

式(33)中：

(34)

Γ(n+1)=n!.

(35)

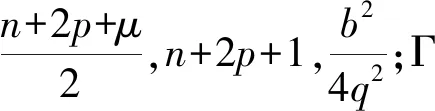
对式(27)作进一步处理，得到Lommel-Gauss光束传输的二阶非傍轴修正光场为

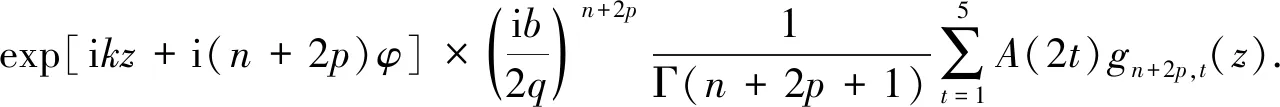
(36)

对应系数如下:

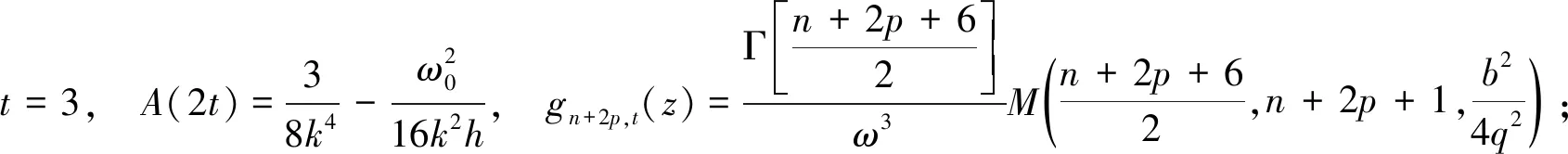
同理，可得到一阶非傍轴修正光场为

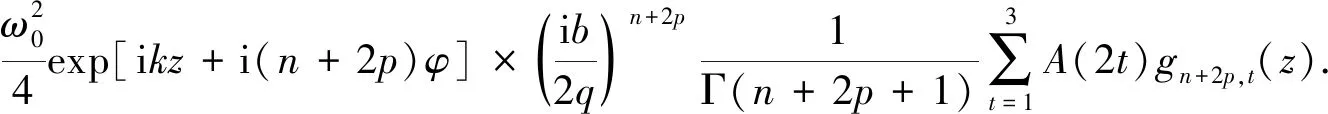
(37)

零阶非傍轴修正光场为

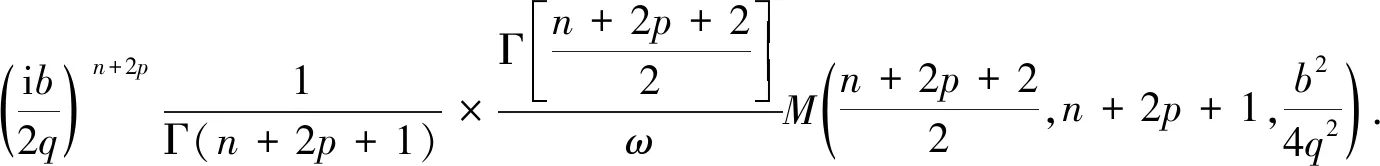
(38)

式(38)给出的零阶非傍轴修正光场就是Lommel-Gauss光束传输傍轴的近似解.利用式(36)～式(37)给出的一阶、二阶非傍轴修正光场，可用于较为精确计算Lommel-Gauss光束非傍轴传输或近场传输的轴上光场分布.

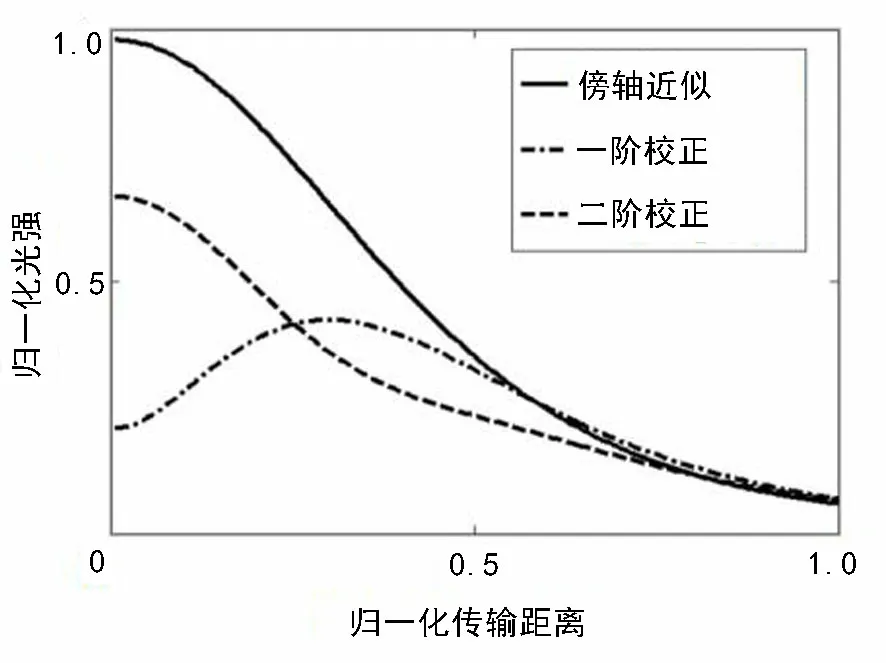
图1 Lommel-Gauss光束轴上光强分布

基于Lommel-Gauss光束轴上光场的零阶、一阶、二阶非傍轴修正解式(36)～式(38)，取参数λ=632.8 nm,β=80 m-1和ω0=60 μm，计算Lommel-Gauss光束传输过程中的轴上强度分布.计算过程中，为使计算结果尽可能精确，理论上p值的选取要尽可能地大，但p值越大，相应的计算时间将增大.不过综观式(36)～式(38)可知，随着p值的增大，求和表达式中的高阶项对光强分布的影响将会越来越小.实际上，p>50的高阶项基本不再影响光强分布的计算结果.本文取p=200，计算结果如图1所示.从图1中可看出，Lommel-Gauss光束在传输过程中，当传输距离较小时，发现傍轴近似结果和利用本文所推导的非傍轴修正表达式得到的结果存在较大差异.显然，基于衍射理论研究光束近场传输时，非傍轴计算结果更为精确.但是，非傍轴理论较傍轴理论数学计算过程更为复杂.本文基于虚源技术给出的Lommel-Gauss光束的非傍轴传输校正项，对于精确、解析研究任意n阶Lommel-Gauss光束的非傍轴传输有较为重要的理论价值.而随着传输距离的增加，非傍轴修正后的计算结果与傍轴近似解越来越接近.这也意味着，当研究光束的远场传输时，可以用傍轴近似解替代非傍轴修正解.以上结论与经典的光学理论的相关论述相一致[15-19].此外，非傍轴修正后的计算结果与傍轴近似解在远场计算结果的一致性，也间接证明了本文推导的Lommel-Gauss光束非傍轴传输表达式的正确性.

3 结 论

依据光束传播的独立性和叠加性原理，准无衍射Lommel-Gauss光束可以展开为无穷项Bessel光束的叠加形式.由于Bessel函数理论非常成熟，这为我们借助Bessel光束的性质研究Lommel-Gauss光束在自由空间中的传输特性提供了便利.本文通过引入一组能够产生n阶Lommel-Gauss光束的虚光源点，利用虚源法、格林函数法和Fourier-Bessel变换理论，通过建立对应的非齐次亥姆霍兹方程，计算得到n阶Lommel-Gauss光束的非傍轴传输严格积分表达式.利用该积分表达式推导给出了Lommel-Gauss光束轴上光场分布的解析表达式.以二阶非傍轴修正为例，得到n阶Lommel-Gauss光束保留到二阶非傍轴修正项的轴上光场分布图.本文给出的准无衍射Lommel-Gauss光束非傍轴传输的解析表达式，为将这种新型光束更好地用于实际的科学研究奠定了理论基础.