广义复梯度下的Schwarz-Pick引理*

王 根, 刘 洋

(浙江师范大学 数学与计算机科学学院,浙江 金华 321004)

0 引 言

近年来，与各种全纯映射相关的Schwarz-Pick引理理论得到了迅速发展.其中涉及到一些常见的例子,如从单位圆到某些经典域的映射[1-2]、从多圆到单位球的映射[3-4]、经典域上的有界全纯函数及Berezin算子演算的分析与高阶Schwarz-Pick之间的相互作用[1,4-5].Schwarz引理是解析函数的重要定理,对于共形映射的建立有很大作用;它表明当经典解析映照后,从原像域到像域之间的有趣变化,给出了从给定域确定对象域的有效估计.然而,复数域本身的结构性质对其上的复函数的直接影响几乎没被报道，复数域本身的结构直接有效地影响了复函数的全纯性质与稳定方面的特征.

本文引进了与复数域直接相关的结构函数，讨论了更为普遍的全纯性质与复函数所要遵循的理论形式,研究了一般复函数变换意义下的结构复微分与广义复梯度所遵循的结构性质,并利用新的算子讨论了广义复梯度下的Schwarz-Pick引理等相关理论,此时Schwarz-Pick引理只是作为它的一个特例.

1 预备知识

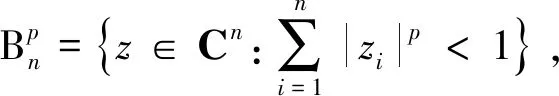
定理1(Schwarz引理)[7]若f∈Hol(U,U),且f(0)=0,则|f(z)|≤|z|,|f′(0)|≤1,|f′(0)|=1当且仅当f(z)=zeiτ,τ∈R.

引理1[2-6]单位圆盘U中的经典Schwarz-Pick引理的结果为[2-6]

(1)

对于全纯映射f:U→B,已经证明了

(2)

对于全纯映射f:U→Bm,已经证明了

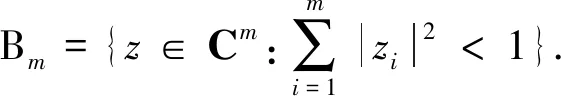
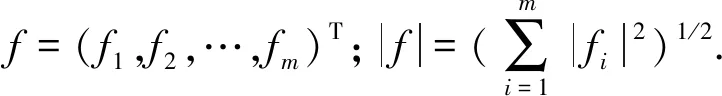
(3)

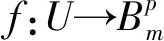
引理2[1-2]对于给定的全纯映射g:X→Y，有

以及X∈C,Y∈Cm.

为方便读者查阅，此处加上引理2的证明.具体细节可以参阅文献[1-2].

其中，p为奇数或偶数.具体可参阅文献[1].对于g(z)=0的情况可以参阅文献[2].引理2证毕.

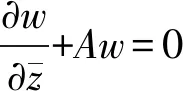
2 主要结果

接下来考虑如下复函数变换:

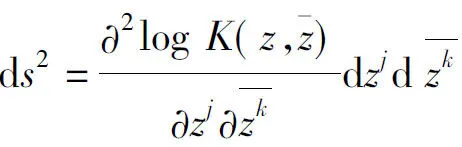
定义1与复数域有关的结构函数s自然地诱导出广义复梯度算子为D=+s,使得复梯度变换为g(z)→Dg(z)=g(z)+g(z)s,则复函数g(z)的广义复梯度为

Dg(z)=g(z)+g(z)

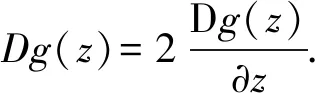
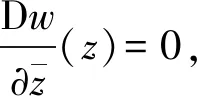
结构全纯条件可以求出具体复函数的解形式为

(5)

由引理3得到它的解为w(z)=Φ(z)e-s(z).现在对解进行Taylor展开,得到

(6)

定理4对于给定的结构全纯映射g∈Shol:X→Y有

证明 由引理2的证明过程可得

因而由广义复梯度算子关系式可以得到

D‖g(z)‖=‖g(z)‖+‖g(z)‖

显然，上式为g(z)≠0的情况.

若g(z)=0,则广义复梯度退化为普通复梯度Dg(z)=g(z),结构全纯函数(5)退化为普通全纯条件此时原先结果在g(z)=0时保持不变.根据式(3)，由Fréchet导数知,对β∈C且定理4证毕.

事实上，‖g(z)‖在广义复梯度D下有具体的表达形式D‖g(z)‖=‖g(z)‖+‖g(z)‖以及|D‖g(z)‖|=‖g′(z)‖,g(z)=0,根据复数的不等式表述可以得到

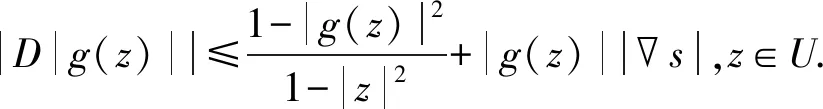
以下设复函数的模q=|w(z)|,利用结构复微分和广义复梯度算子得到如下和结构函数有关的推广形式:

定理5(广义Schwarz-Pick引理) 设f∈Shol:U→U,则

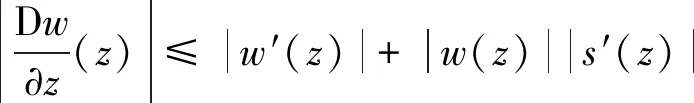
显然,若s′(z)=0,则广义Schwarz-Pick引理退化到经典Schwarz-Pick引理.

同样，对于结构全纯映射f∈Shol:U→B,仿照上述广义Schwarz-Pick引理的证法,易得q在广义复梯度D下的形式为

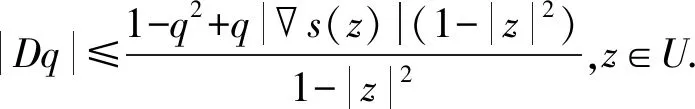
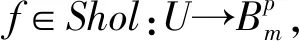
3 结 语

首先通过复函数结构变换得到了结构复微分与广义复梯度,得到了具有普遍性的广义结构Wirtinger导数算子、与结构函数息息相关的广义Schwarz-Pick引理,以及依赖于结构函数的解w(z)=Φ(z)e-s(z).事实上,定理2和定理3均可以通过这种技术延拓到包含复数域上结构函数的广义形式，只需要将普通梯度算子改换成广义复梯度D=+s就行.