刍议“基本图形”在初中几何教学中的应用
2019-06-25包贤明
包贤明

摘要:与小学数学相比,初中对平面图形学习从简单的、静止的、直观的慢慢转变成了复杂的、运动的、抽象的。其研究的难度和深度都有了大幅度提高,这对于学生的思维表现能力和逻辑发展能力也都有了更高的要求,在这种情况下,我们应更加重视“基本图形”的教学和深度挖掘,并引导学生对几何题型探索和解题方法提炼,可以较为有效地进行数学教学。
关键词:基本图形;初中数学;平面几何;数学学习
中图分类号:G633.6 文献标识码:A 文章编号:1992-7711(2019)01-0014
一、平面几何的学习现状
初中数学平面几何主要研究图形的形状、大小和性质,和小学数学相比,其研究难度和深度都有了大幅度提高,图形学习从简单的、静止的、直观的慢慢转变成了复杂的、运动的、抽象的。这对于学生的思维表现能力和逻辑发展能力也都有了更高的要求,数学学习也追求“活学活用”,创新多变的“新颖”题目也不断出现,这也引导着数学几何的变革方向。那么,在平面几何教学中,有没有更加高效的方法呢?有没有方法可以让学生能更好地理解抽象的数学几何概念定理?笔者认为,在数学教学中,应更好地发挥“基本图形”的引领作用,引导学生整理归纳各类“基本图形”,揭示它背后所蕴含的数学知识和提炼解题方法,可以较为有效地开展数学教学。
二、解决的策略
1. 建立“基本图形”与几何知识的双向关联
在教学过程中把基本的定义定理以“基本图形”的形式反映出来,建立最基本的基本图形库,要让学生一想到几何知识就联想到与之相关的几何图形,看到几何图形就想到相应的几何知识,改变那种把性质定理的文字表述与图形割裂开的学习方法。
建立“基本图形”与几何知识的双向关联,是分析解决问题的先决条件,没有这种基本的关联,训练思维能力就缺少了必要载体。如一提到平行线的性质和定理就联系到“三线八角”基本图形,一提到垂径定理就联想到右图基本图形,这种“基本图形”本身就是“定义定理”的组合部分,它是教师传授几何知识的载体,也是学生加深概念印象和灵活运用几何定理的“图示”。
2. 归纳整理各类习题中出现的“基本图形”
尽管数学练习千变万化,但是绝大多数题目都能从中提炼出一些基本元素,教师在教学中帮助学生梳理、提炼这些“基本图形”,遇到问题时分离这些“基本图形”,在“基本图形”残缺时,构造“基本图形”,可以以这些“基本图形”为载体,培养学生的空间想象能力,分析推理能力。
当然,这种整理归纳不仅是对“基本图形”的提炼,也包括揭示各图形之间的联系和区别,把各个基本图形置于网状结构中系统排布,让学生感知各知识板块之间的变化和联系。
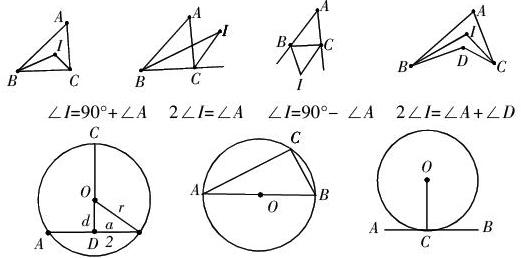
如下图是三角形和角平分线结合下的“基本图形”,其图形变化一脉相承,而结论运用也简练方便。在△ABC、飞镖形、八字形中,BI、CI分别是内或外角平分线,∠BIC与其余各角分别有以下的关系:
3. 注重对“基本图形”的提炼,渗透数学思想方法和解题技巧
如果说教学和看书一样都经历由薄到厚、再由厚到薄的过程,那最后的“薄”就是“基本图形”,而很多几何题型都是以一个或几个“基本图形”按照一定的“组织形式”而形成的,这些基本图形承载着题型的考点内容和解题方向。这些图形存在某种类似,但求证的结论有所不同,而其解法和技巧基本都是一致的,同時这类题型所演变的大量题目的解题技巧基本都是一致的,这类题完全可以归为一类。
4. 整理与“基本图形”有关的几何辅助线的常规添法
通过添加“辅助线”解题是学生解题的难点,但是“常规辅助线”的添加也正是基于“基本图形”的基础之上,系统研究几何基本图形,可以让学生根据考题信息检索到考点知识以及与考点知识所对应的图形,从而自然而然添加辅助线。
在解决与圆有关的问题时,常常需要添加适当的辅助线,架起题设和结论间的桥梁,从而使问题化难为易,顺其自然地得到解决,例如:(1)见弦作弦心距;(2)见直径作圆周角;(3)见切线作半径。而这三种辅助线添法,对应着如下三个“基本图形”。
三、“基本图形”对教学的作用
1. 有利于学生解题思维的发展
在初中数学几何中,“基本图形”就像一块块“预制板”,是数学几何大厦的基本模块。通过掌握“基本图形”,学生既可以理解数学知识的由来,也可以掌握性质定理所衍生的推论以及习题中所常用到的基本结论。学生学习的核心在于“解题能力”的提升,如果学生能掌握“基本图形”,对其解题思路的拓展都有着积极作用。
2. 有利于解题时探求思路拓宽条件
“基本图形”是和数学知识的双向关联,每个基本图形都对应着一类几何知识,并且其背后的结论也都是固定的,事实上,几何“题型”很多都是几个“基本图形”的组合应用,只要我们能挖掘每个“基本图形”背后的探究思路就能大致理出这类“题型”的解决方向。“基本图形”对学生解题思路的拓展也体现在“辅助线”的添法上,这也是我们研究的重点。
3. 有利于学生构建网状的几何知识体系
数学教学主张在网状的知识结构图中进行联系教学,而几何基本图形之间的承接和变化都是一脉相承的,并且“基本图形”可以帮助学生整合题型,这有利于学生对数学知识点进行分类检索,符合建构主义理论。
4. 有利于让学生深入感受数学思想方法
数学教学的核心在于思想方法的渗透,对于很多学生而言,思想方法是空洞无物、束之高阁的,而细心研究几何“基本图形”,既可以感受大量的“数形结合”思想,也可以从图形的演变过程中感受“类比迁移”“化归”等重要思想,并且很多几何题目辅助线的添法或者解题方法本身就是数学思想方法推导下的产物,如角平分线的解题思路在于“对称”的思想方法。
5. 有利于促进教师的成长
优秀教师不仅需要具有专业的数学知识、心理学教育学,更需要理解数学知识内部的联系和区别,必须具有一定的教学高度,才能整合知识、高屋建瓴,让学生自然而然地掌握所学知识,做到水到渠成。数学几何“基本图形”是数学抽象符号、定义定理的直观图形,对于教师而言,每个图形都对应着相应的教学知识点。在几何教学中,探究这些“基本图形”对教师成长都有着积极的作用。
综上所述,教师在平时的数学教学中应更加重视“基本图形”的教学,在课堂上或习题课中,教师应有意识的对平面几何基本“图形”进行整理、挖掘、引导学生归纳、提炼解题方法等,这对学生的数学学习,尤其是平面几何的学习,为学生建立平面几何知识体系,形成数学思想方法有着积极而深远的意义。
参考文献:
[1] 吴晓华,谈基本图形在初中几何教学中的应用[J].学科活动,2014(5).
(作者单位:浙江省桐乡市乌镇中学 314500)
