夹心半群T(X,Y,θ)上的一个同余链

2019-06-24薛玲霞孙垒

纯粹数学与应用数学 2019年1期

薛玲霞,孙垒

(1.郑州旅游职业学院基础部,河南郑州 450009;2.河南理工大学数学与信息科学学院,河南焦作 454000)

1 引言

文献[1]建立了从α-半群T(X)(即T(X)⊆TX且包含TX中所有常值变换和集合X上的恒等变换idX)的同余格C(T(X))到集合X上的T-等价关系格Teq(X)的映射γ和从Teq(X)到C(T(X))的映射C,确定了某些拓扑空间X上的所有连续自映射(关于映射的复合)所成的半群S(X)上的最小真同余.文献[2]证明了γ和C都是格同态,并且对于X上的每个T-等价关系E,γ−1(E)是同余格C(T(X))的完全子格.在这个完全子格γ−1(E)中,最大同余是α-同余,即

文献[3]确定了完全子格γ−1(E)中的其它同余.

定义1.1[4]设X,Y是两个非空集合,θ是从Y到X的一个映射.对于从X到Y的映射f,g,定义乘法运算f◦g=fθg,其中fθg表示三个映射在一般意义上的复合.在这个运算下,所有从X到Y的映射构成一个半群,记为T(X,Y,θ).并且T(X,Y,θ)称为(关于夹心映射θ的)夹心半群.

为得到T(X,Y,θ)上的一些同余,现在给出集合Y上与T(X,Y,θ)相联系的一类等价关系.

定义1.2[4]设T(X,Y,θ)是夹心半群,E是集合Y上等价关系.若对于任意的 (a,b)∈E和f∈T(X,Y,θ),有 (fθ(a),fθ(b))∈E成立,则称E是Y上Tθ-等价关系.

由文献 [4]知Y上的所有Tθ-等价关系的集合作成一个格.这个格中包含Y上两个平凡的Tθ-等价关系△(Y)和Y×Y,其中△(Y)表示Y×Y的对角线,即{(y,y):y∈Y}.并且,文献[4-5]将同态

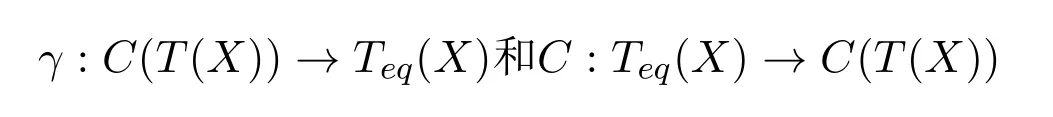
推广到夹心半群T(X,Y,θ)的同余格C(T(X,Y,θ))和集合Y上的Tθ-等价关系格上,建立了格同态

得到了如下结论.

定理1.1[4-5]设T(X,Y,θ)是夹心半群.定义γ:C(T(X,Y,θ))→Teθq(Y)为

其中ρ∈C(T(X,Y,θ)),表示将X中所有点映成y∈Y的常值映射,则γ是单调的满的格同态.定义C:为

根据定理1.1,文献 [4-5]讨论了夹心半群T(X,Y,θ)上的两个同余,即骨架同余和α-同余,刻画了它们的特征,得到了如下的定理.

定理1.2[4-5]对于任意,则γ−1(E,θ)是C(T(X,Y,θ)) 的一个完全子格.并且这个子格的最小同余是骨架同余

最大同余是α-同余Cα(E)={(f,g):∀y∈Y,(fθ(y),gθ(y))∈E}.

本文中用Z(Y)表示所有从X到Y的常值映射.Y/E表示Y上由Tθ-等价关系E决定的Y的分类.表示x所在的E类,即x∈∈Y/E.fθ(Y)表示从Y到Y的复合映射fθ的象集.对每个f∈T(X,Y,θ),令π(fθ)表示由复合映射fθ决定的Y的分类,即π(fθ)={(fθ)−1(y):y∈fθ(Y)}.

没有特殊说明,本文中Y上Tθ-等价关系E都是非平凡的,即E△(Y)且EY×Y.文中没作说明的概念与符号,参看文献[4-5].

2 几个引理

本节给出几个相关的引理.

引理2.1 设f∈T(X,Y,θ),E是Y上Tθ-等价关系,则对于任意B∈Y/E,存在

证明在B中取定一点b.设fθ(b)=b′.记b′所在的E类为B′.在B中任取一点x,则 (x,b)∈E.注意到f∈T(X,Y,θ),,则 (fθ(x),fθ(b))∈E,即fθ(x)∈B′.由x的任意性知fθ(B)⊆B′.

由引理 2.1知对于任意B∈Y/E,则 (fθ)−1(B)=∅或 (fθ)−1(B)是Y中一些E类的并.

引理2.2 设E是Y上Tθ-等价关系,σ是T(X,Y,θ)上的同余且σ ∈ γ−1(E,θ),则对于任意A∈Y/E和任意(f,g)∈σ,存在B∈Y/E,使fθ(A)⊆B,gθ(A)⊆B.

证明由引理 2.1知,对于任意A∈Y/E,存在B∈Y/E,使fθ(A)⊆B.由于

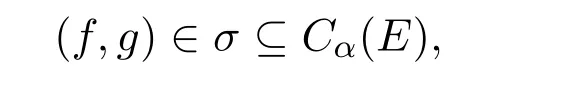
于是对于任意x∈Y,有(fθ(x),gθ(x))∈E.特别地,对于A中的任意一点a,有

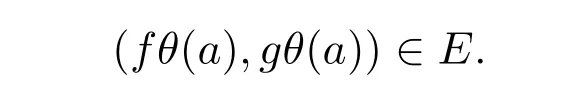
注意到fθ(a)∈B.因此gθ(a)∈B.由a的任意性知gθ(A)⊆B.

引理2.3 设f,g∈T(X,Y,θ)且E是Y上Tθ−等价关系.若

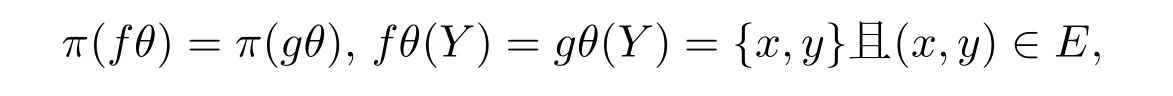
则对于任意h∈T(X,Y,θ),有

证明首先证明

若hθ(x)=hθ(y),则 (h◦f)θ=(h◦g)θ,即π((h◦f)θ)=π((h◦g)θ).

若hθ(x)̸=hθ(y),则π((h◦f)θ)=π(fθ)=π(gθ)=π((h◦g)θ).

下面证明π((f◦h)θ)=π((g◦h)θ).分两种情形.

情形1 若fθ|hθ=gθ|hθ,则 (f◦h)θ=(g◦h)θ.故π((f◦h)θ)=π((g◦h)θ).

情形2 若fθ|hθ̸=gθ|hθ,则fθ̸=gθ. 由于

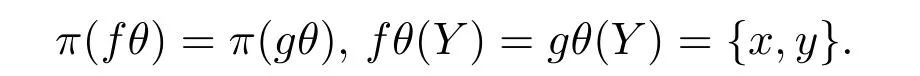
于是

此时又有三种可能.

(P1)若hθ(Y)⊆(fθ)−1(x),则

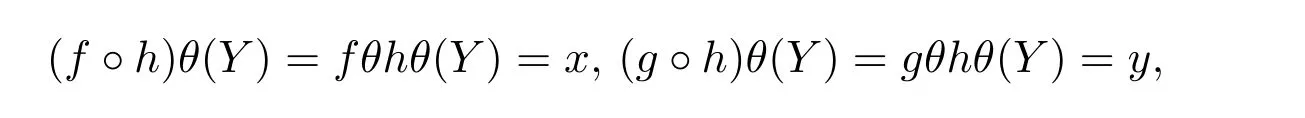
即

于是

则A,B是Y的两个非空子集,且于是

这表明π((f◦h)θ)=π((g◦h)θ).

因此,不管何种情形都有π((f◦h)θ)=π((g◦h)θ).

引理2.4 设T(X,Y,θ)是夹心半群,E是Y上Tθ-等价关系.设

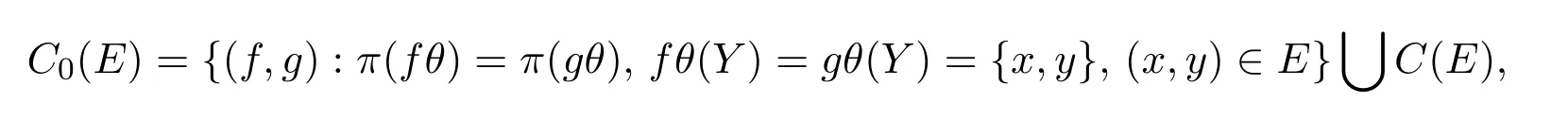
则C0(E)是T(X,Y,θ)上的一个同余且C0∈ γ−1(E,θ).

证明显然C0(E)是T(X,Y,θ)上一个等价关系,并且C0∈ γ−1(E,θ).设

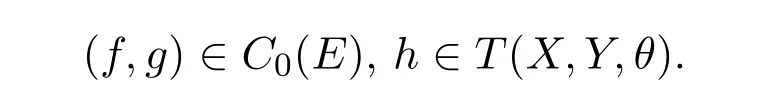
若 (f,g)∈C(E),由C(E)是T(X,Y,θ)上的同余知

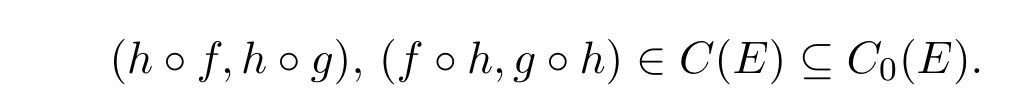
若h∈Z(Y).设h=,则

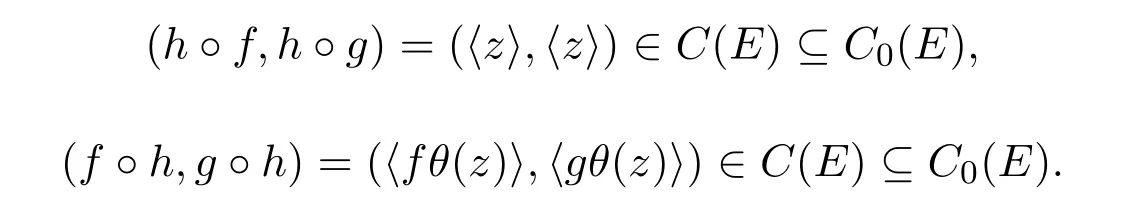
下面考虑(f,g)(E)(Y).由引理2.3知π((h◦f)θ)=π((h◦g)θ)且

由于 (x,y)∈E,h∈T(X,Y,θ),于是 (hθ(x),hθ(y))∈E.这表明C0(E)是左同余.

另一方面,由引理 2.3知π((f◦h)θ)=π((g◦h)θ).此时又有两种可能.

(P1)若 (f◦h)θ(Y)=fθhθ(Y)={x,y}.注意到π((f◦h)θ)=π((g◦h)θ).于是

这表明若 (f◦h)θ(Y)={x,y},则 (g◦h)θ(Y)={x,y}.于是 (f◦h,g◦h)∈C0(E).

(P2) 若 (f◦h)θ(Y)={x},则 (g◦h)θ(Y)=y. 这表明若则.于是 (f◦h,g◦h)∈C(E)⊆C0(E).

因此,不管何种情形,都可以证明C0(E)是右同余.故C0(E)是T(X,Y,θ)上的同余.

引理2.5 设T(X,Y,θ)是夹心半群,E是Y上Tθ-等价关系.设

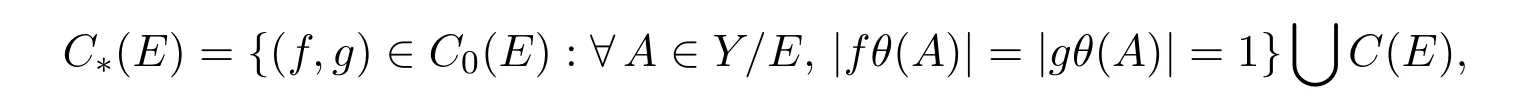
则C∗(E)是T(X,Y,θ)上的一个同余且C∗∈γ−1(E,θ).

证明显然C∗(E)是T(X,Y,θ)上一个等价关系,并且C∗∈ γ−1(E,θ).设

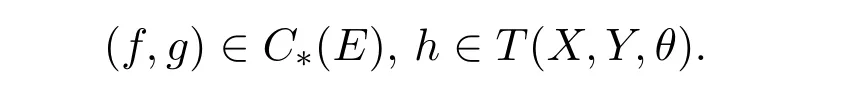
若 (f,g)∈C(E),由C(E)是T(X,Y,θ)上的同余知

下面考虑(f,g)(E).对于任意A∈Y/E,有

这表明 (h◦f,h◦g)∈C∗(E).于是C∗(E)是左同余.

另一方面,由引理2.1知对于任意A∈Y/E,存在B∈Y/E,使hθ(A)⊆B.于是

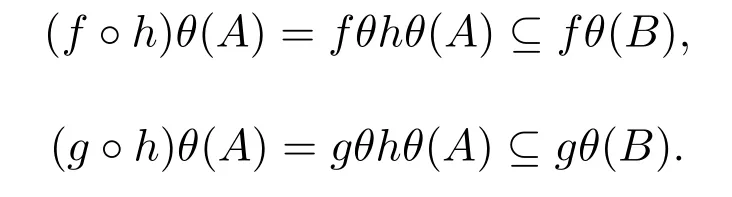
注意到 (f,g)∈C∗(E),于是|fθ(B)|=|gθ(B)|=1.从而

这表明 (f◦h,g◦h)∈C∗(E),即C∗(E)是右同余.从而C∗(E)是T(X,Y,θ)上的一个同余.

3 主要结论

有了上节的几个引理作为准备,本节给出主要定理.

在叙述结论之前介绍一些符号.设f是夹心半群T(X,Y,θ)的任意映射,E是Y上的Tθ-等价关系.记RE(fθ)={A∈Y/E:(fθ)−1(A)̸=∅}.用|fθ|E表示RE(fθ)的基数.

定理3.1 设T(X,Y,θ)是夹心半群,E是Y上Tθ-等价关系,|Y/E|=m.对于1≤k≤m,设

则Ck是T(X,Y,θ)上的同余,并且

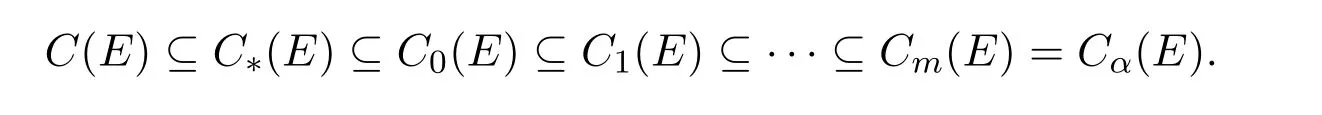
证明对于 1≤k≤m,显然Ck(E)是T(X,Y,θ)上等价关系.在Ck(E)中任取 (f,g)且.在T(X,Y,θ)中任取h.下面分两种情形.

情形1 若h∈Z(Y).设则于是

对于任意A∈Y/E且,则 ((h◦f)θ)−1(A)=((h◦g)θ)−1(A)=∅.并且

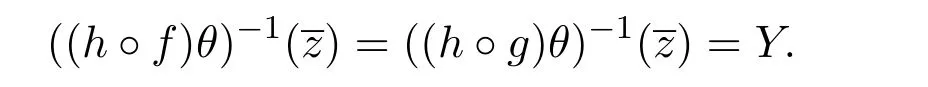
是Ck(E)是左同余.

由 (f,g)∈Ck(E)知即对于任意

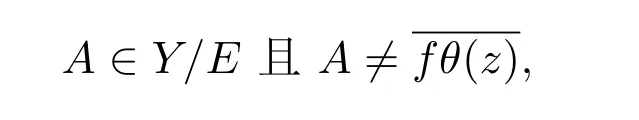
则 ((f◦h)θ)−1(A)=((g◦h)θ)−1(A)=∅.此外,

于是Ck(E)是右同余.

情形2若设A∈Y/E且由引理2.1知(hθ)−1(A)是Y中一些E类的并.设其中Bi∈Y/E.由于

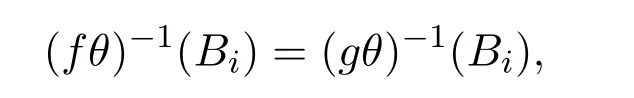
于是

进而RE((h◦f)θ)=RE((h◦g)θ),即|(h◦f)θ|E=|(h◦g)θ|E.

下面证明|(h◦f)θ|E≤k. 设RE(fθ)={Cj}j∈J,其中Cj∈Y/E,|J|≤k.由(f,g)∈Ck(E)知

由引理 2.1知对于任意Cj,存在Dj,使hθ(Cj)⊆Dj.于是

从而|(h◦f)θ|E=|(h◦g)θ|E≤|(fθ)|E≤k.因此Ck(E)是左同余.

对于任意A∈Y/E,有 (fθ)−1(A)=(gθ)−1(A). 于是

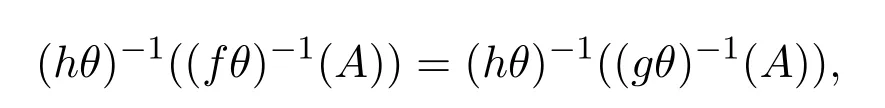
即 ((f◦h)θ)−1(A)=((g◦h)θ)−1(A),|(f◦h)|E=|(g◦h)|E.注意到

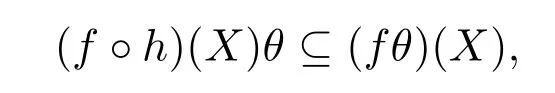
则|(g◦h)|E=|(f◦h)|E≤|fθ|E.因此Ck(E)是右同余.故Ck(E)是同余.

其次证明对于 1≤k≤m,有Ck(E)∈γ−1(E,θ),为此只需要证明γ(Ck(E))=E.

于是γ(Ck(E))=E.故Ck(E)∈γ−1(E,θ).

最后证明Cm(E)=Cα(E),为此只需要证明Cα(E)⊆Cm(E).由于|Y/E|=m,于是Cm(E)={(f,g):∀A∈Y/E,(fθ)−1(A)=(gθ)−1(A)}.在Cα(E)中任取 (f,g),设存在B∈Y/E, 使由引理 2.1 知 (fθ)−1(B),(gθ)−1(B)是Y中一些E类的并.取C∈Y/E,即且则