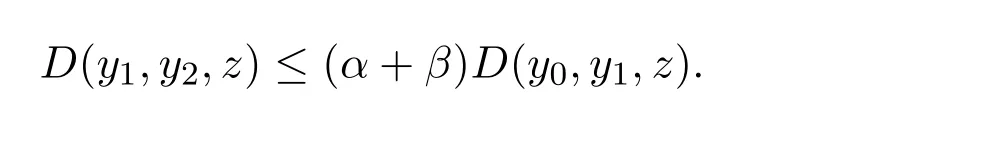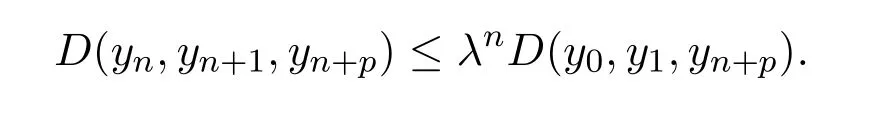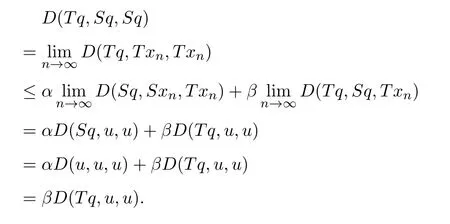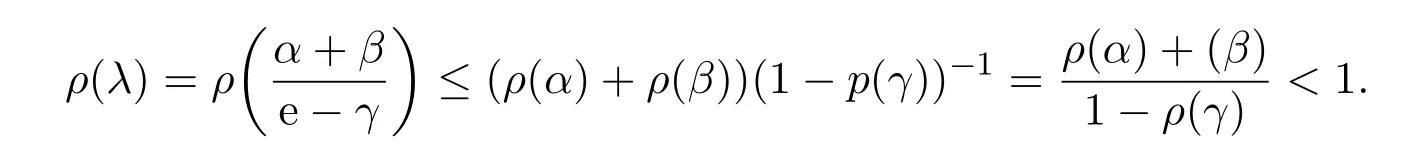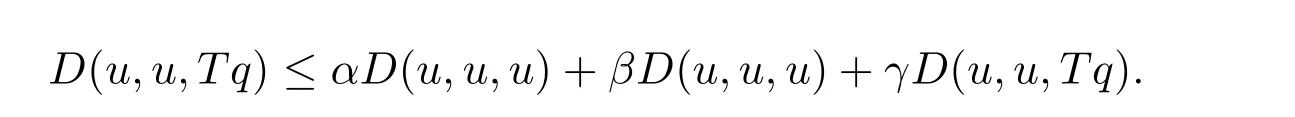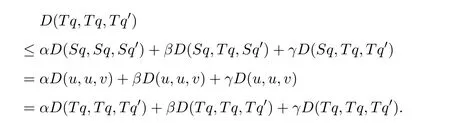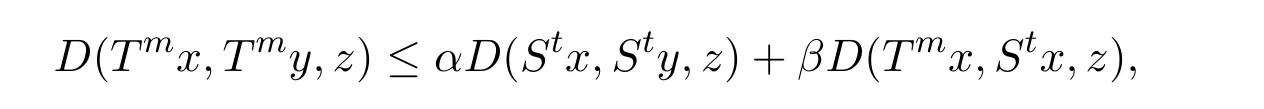具有Banach代数的锥D-度量空间和公共不动点定理
2019-06-24张学智薛西锋
张学智,薛西锋
(西北大学数学学院,陕西 西安 710127)
1 引言
1922年,Banach提出著名的压缩映象原理[1].1992年,文献[2]引入D-度量空间的定义,并在完备有界的D-度量空间中证得压缩映射的不动点定理.1996年,文献[3-4]给出相容映象的定义,并证明了相容映象具有公共的不动点,此外也有大量作者对多个相容映象的公共不动点问题作出研究[5-6].受Jungck的启发,文献[7]在D-度量空间中引入相容映象的概念,并证明了D-度量空间中相容映象的公共不动点定理.
2007年,文献[8]用序Banach空间代替实数,引入了锥度量空间,一些学者在此空间中得到了单个自映射的不动点定理和多个相容映象的公共不动点定理[9-10].2013年,文献[11]用Banach代数代替序Banach空间得到具有Banach代数的锥度量空间,与度量空间相比较,其空间结构发生了改变.近来,许多作者在删去锥的正规性条件后,用不同的方法在不动点理论方面作出新的研究.
基于以上内容,本文将锥D-度量和Banach代数糅合在一起,得到具有Banach代数的锥D-度量空间的定义,并在删去锥的正规性的条件下证得2个相容映象的公共不动点定理,主要结果改进了已有文献的一些结论.
2 预备知识
设A为实的Banach代数,即A是具有乘法运算的实Banach空间,其运算具备以下性质(对任意的x,y,z∈A,α∈R,):(1)(xy)z=x(yz);(2)x(y+z)=xy+xz;(3)α(xy)=(αx)y=x(αy);(4).
本文总假设实Banach代数A具有单位元(即乘法单位元)e,满足对任意x∈A均有ex=xe=x.一个元素x∈A称为可逆的,如果存在一个元素(称为它的一个逆元)y∈A使得xy=yx=e.x的逆元记作x−1.更详细的内容可以参照文献[12].
下面是本文用到的一些重要的定义和引理.
引理2.1[12]设A是具有单位元 e的 Banach代数,x∈A.若x的谱半径ρ(x)<1,即.则e−x是可逆的,并且有.

注记2.1[13]若ρ(x)<1,则∥xn∥→0(n→ ∞).
引理2.2[13]设A是具有单位元e的Banach代数,x,y∈A.若x和y可交换,则有下列式子成立:
(1)ρ(xy)≤ρ(x)ρ(y);
(2)ρ(x+y)≤ρ(x)+ρ(y);
(3)|ρ(x)−ρ(y)|≤ρ(x−y).
引理2.3[13]设A是具有单位元e的Banach代数,k∈A.若0≤ρ(k)<1,则

定义2.1[8]设A是具有单位元 e的 Banach代数,A的一个非空闭凸子集P称为锥,若 (1){θ,e}⊂P;(2)αP+βP⊂P对任意的非负实数α,β均成立;(3)P2=P·P⊂P;(4)P∩(−P)={θ}.其中θ为Banach代数A中的零元.对于A中的锥P,定义半序≤如下:x≤y当且仅当y−x∈P;x 下文假定P为Banach代数A中的体锥,≤是由在P中定义的半序,N是自然数集. 定义 2.2 设X是非空集合,若映射D:X×X×X×X−→A满足: (1)θ≤D(x,y,z)对任意x,y,z,a∈X成立,D(x,y,z)=θ当且仅当x=y=z; (2)D(x,y,z)=D(x,z,y)=D(y,x,z)=···; (3)D(x,y,z)≤D(x,y,a)+D(x,a,z)+D(a,y,z),对任意x,y,z,a∈X.则D称为X上的锥D-度量,(X,D)称为具有Banach代数的锥D-度量空间. 下面给出一个具有Banach代数的锥D-度量空间的例子. 例2.1 设对任意的x∈A.定义乘法运算为xy(t)=x(t)y(t),t∈[0,1],则A是具有单位元e的Banach代数. 设P={x∈A:x(t)≥0,t∈[0,1]},则P⊂A是一个非正规体锥[14]. 令X=[0,1],定义映射D:X×X×X×X−→A如下: 则(X,D)是具有Banach代数A的锥D-度量空间. 定义2.3 设(X,D)为具有Banach代数A的锥D-度量空间,x∈X且{xn}为X中的序列,则 (1)称{xn}收敛于x,若对任意满足θ≪c的向量c∈A,存在正整数N,使得D(xm,xn,x)≪c对任意m,n>N成立,记为 (2)称{xn}为Cauchy列,若对于任意满足θ≪c的向量c∈A,存在正整数N,使得D(xn,xn+1,xn+p)≪c对任意n,p≥N成立. (3)称(X,D)为完备的锥D-度量空间,若(X,D)中的每一个Cauchy列在(X,D)中都收敛. 定义2.4 设(X,D)是具有Banach代数A的锥D-度量空间,称X是D-有界的,若存在M≥0,使得D(x,y,z)≤M对任意的x,y,z,a∈X成立,M称为X的D-有界数. 引理2.4 设(X,D)是具有Banach代数A的锥D-度量空间,则 是连续的.即若 则 引理2.5[14-15]设E是具有体锥P的Banach空间,若θ≤u≪c对任意θ≪c成立,则u=θ. 引理2.6[14-15]设E是具有体锥P的Banach空间,{xn}∈A.若 则对任意θ≪c,存在正整数N使得xn≪c对任意n≥N成立. 定义2.5[16-17]设X是非空集合,映射T,S:X→X,若存在x∈X使得w=Tx=Sx,则称w是T和S的叠合点. 定义2.6[18]设X是非空集合,映射T,S:X→X称为弱相容的,对任意x∈X,如果Tx=Sx,都有TSx=STx成立. 引理2.7[16-17]设X是非空集合,映射T,S:X→X是弱相容的,若T,S在X中有唯一的叠合点w,即w=Tx=Sx,则w也是T和S的唯一公共不动点. 定理3.1 设(X,D)是具有Banach代数的完备有界的锥D-度量空间,M是X的D-有界数,P是A的非正规体锥,若映射T,S:X→X满足 对任意的x,y,z∈X,其中α,β ∈P且 0≤ ρ(α)+ρ(β)<1,α,β可互换,此外,设有 (1)T(X)⊂S(X); (2)S(X)是X的闭子空间; (3)(T,S)是弱相容的. 则T,S在X中有唯一的公共不动点. 证明任选x0∈X,由T(X)⊂S(X),可构造序列{xn}和{yn}满足 不妨设ynyn+1,n∈N,下证{yn}是 Cauchy列. 对任意的z∈X,有 由此得到 令λ=α+β,同理,有 依次进行此过程,可得 对任意固定的P∈N,存在yn+p∈X使得 又因为 由注记 2.1,可得→0(n→∞). 由于M是X的D-有界数,故 故由引理 2.6知,对任意c∈A且θ≪c,存在正整数N使得对任意的n>N时,有θ≤D(yn,yn+1,yn+p)≪c成立. 因此,{yn}是X中的Cauchy列.由于S(X)是完备空间X的闭子空间,故S(X)也是完备的,因而存在u∈S(X)使得,从而,下证u是T,S的唯一的叠合点. 由于u∈S(X),知存在q∈X使得Sq=u.首先证Tq=Sq=u.因为D是连续的,所以有 又D(Tq,Sq,Sq)=D(Tq,u,u),故 (e−β)D(Tq,u,u)≤θ. 于是D(Tq,u,u)=θ,因此Tq=u=Sq,即u为T,S的叠合点.下证u的唯一性,不妨设v=Tq′=Sq′为T,S的另一叠合点,有 化简得 (e−α)D(u,v,u)≤θ.故D(u,v,u)=θ,即u=v.所以u是T,S的唯一的叠合点.根据引理2.7,由T,S的弱相容性,知u是T,S的唯一的公共不动点. 定理3.2 设(X,D)是具有Banach代数的完备有界的锥D-度量空间,M是X的D-有界数,P是A的非正规体锥,对任意的x,y,z∈X,若自映射T,S:X→X满足 对任意的x,y,z∈X,其中α,β,γ∈P且 0≤ρ(α)+ρ(β)+ρ(γ)<1,α,β,γ可互换,此外,设有(1)T(X)⊂S(X);(2)S(X)是X的闭子空间;(3)(T,S)弱相容的.则T,S在X中有唯一的公共不动点. 证明任意选定x0∈X,由T(X)⊂S(X),可构造迭代序列{xn}和{yn}满足 不妨设ynyn+1,n∈N,下证{yn}是 Cauchy列. 对任意的n,p∈N,有 于是推出 令 依次进行此过程,有D(yn,yn+1,yn+p)≤λnD(y0,y1,yp). 由于M是X的D-有界数,故又 由引理2.6知,对任意θ≪c且c∈A,存在正整数N使得对任意n≥N时,有 故{yn}是X中的Cauchy列,由X的完备性,S(X)是X的闭子空间知S(X)是完备的,从而存在u∈S(X)使得,也有,下证u是T,S的唯一叠合点.由u∈S(X)知存在q∈X使得Sq=u,首先证明Tq=Sq=u,有 由D的连续性,令n→∞,上式两端同时取极限,可得 可推得 (e− γ)−1D(u,u,Tq)≤θ.因此,D(u,u,Tq)=θ,于是Tq=u=Sq.即u为T,S的叠合点,下证u是唯一的,不妨设v=Tq′=Sq′是T,S的另一叠合点,则有 化简得 (e−α−β−γ)D(Tq,Tq,Tq′)≤θ.则D(Tq,Tq,Tq′)=θ,即u=Tq=Tq′=v,故u是T,S的唯一的叠合点. 又因为T,S是弱相容的,即当u=Tu=Su,有TSu=STu.故由引理2.7知u是T,S的唯一的公共不动点. 推论3.1 设(X,D)是具有Banach代数的完备有界的锥D-度量空间,M是X的D-有界数,P是A的非正规体锥,若自映射T,S:X→X,m,t为正整数,满足 对任意的x,y,z∈X,其中α,β∈P且 0≤ρ(α)+ρ(β)<1,α,β可互换,此外,设有 (1)Tm(X)⊂St(X);(2)St(X)是X的闭子空间;(3)(Tm,St)是弱相容的.则T,S在X中有唯一的公共不动点. 证明由定理2.1知,Tm和St有唯一的公共不动点u.当m=1时,Tu=Stu=u,由条件(3)知,TStu=StTu,所以有Tm(Tu)=T(Tmu)=Tu=T(Stu)=St(Tu),上式说明Tu为Tm,St的公共不动点.由u的唯一性,可得Tu=u. 同理,Su=u.故T,S有唯一的公共不动点. 推论3.2 设(X,D)是具有Banach代数的完备有界的锥D-度量空间,M是X的D-有界数,P是A的非正规体锥,若自映射T,S:X→X,m,t为正整数,满足 对任意的x,y,z∈X,其中α,β∈P且 0≤ρ(α)+ρ(β)+ρ(γ)<1,α,β可互换,此外,设有 (1)Tm(X)⊂St(X);(2)St(X)是X的闭子空间;(3)(Tm,St)是弱相容的.则T,S在X中有唯一的公共不动点. 证明类似于推论3.1.


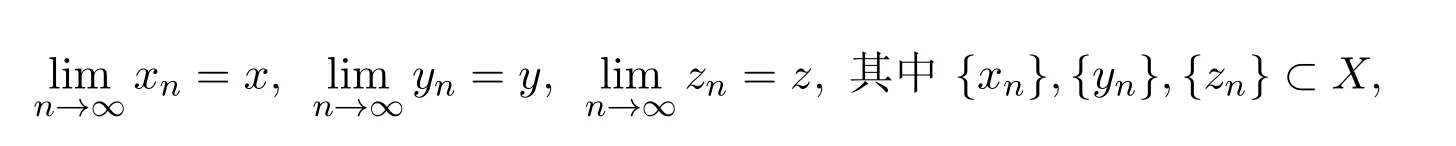
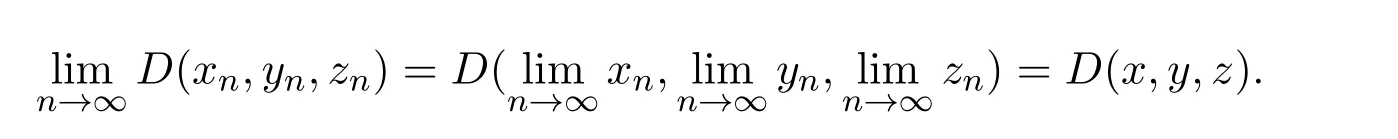
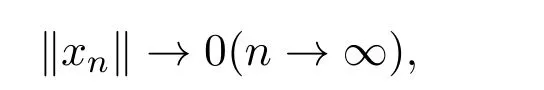
3 主要结果及其证明