以问题为导向，实施有效探究——以椭圆内接三角形面积最大值的探究为例

☉广东省深圳市高级中学 高 军

素养导向的高考命题注重科学探究能力的考查.通过创设新的问题情境，变换设问角度和知识的组合方式，考查学生的科学探究能力.探究性教学是教师创设一定的问题情境，让学生自主参与的学习过程.本文以问题为导向，由浅入深，由简单到复杂，由特殊到一般，层层递进，遵循学生的认知规律，展示了椭圆内接三角形面积最大值的一种探究过程，与同行交流.

问题1：在椭圆上存在三点A，B，C，若AB⊥x轴且△ABC的重心为坐标原点O，求△ABC的面积.

探究：由AB⊥x轴且△ABC的重心为坐标原点O，易得C

问题2：在椭圆上存在三点A，B，C，且△ABC的重心为坐标原点O，求证：△ABC的面积为定值.

探究：当直线AB的斜率不存在时，由问题1得△ABC

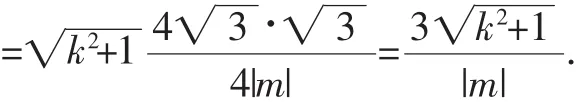
设原点O到直线AB的距离为d1，点C到直线AB的距离为d2，则故△ABC的面积为为定值.

结论1：在椭圆a＞b＞0）上存在三点A，B，C，且△ABC的重心为坐标原点O，则△ABC的面积为定

问题3： 已知椭圆作垂直于 轴的直线x与椭圆E交于A，B两点，点C位于椭圆E上，求△ABC的面积的最大值.

探究：（1）设直线AB的方程为x=t，代入不妨设-2＜t≤0，则点C位于椭圆右端点时，△ABC的面积最大

问题4：已知椭圆E，作直线y=kx+m（m≠0）交椭圆E于A，B两点，设AB的中点为M，延长MO交椭圆于点C，求△ABC的面积的最大值.

结论3：已知椭圆E：，作直线y=kx+m（m≠0）交椭圆E交于A，B两点，设AB的中点为M，延长MO交椭圆于点C，则△ABC的面积有最大值此时△ABC的重心为坐标原点O.

问题5：已知椭圆，求内接于椭圆的△ABC面积的最大值.

探究：（1）若直线AB的斜率不存在时，由结论2得△ABC面积的最大值为，此时△ABC的重心为坐标原点O.

（2）若直线AB的斜率存在时，设直线AB的方程为y=kx+m，将y=kx+m代入a2m2-a2b2=0.