“一题多变性”变式在高三数学复习中的应用——以“求圆锥曲线的离心率”为例

☉安徽省临泉第一中学 曹 丽

复习是高中数学教学的重要组成部分，它既能够帮助学生理清知识脉络，优化头脑中的知识体系，还能够为学生提供思维平台，发散学生的数学思维.然而，传统的高三数学复习课中，出现了“题海战术”“高耗低效”“教师苦，学生累”等不良现象，已经严重影响了学生参与复习活动的积极性与主动性，甚至出现厌倦数学，抵制复习的现象，导致复习课的价值丧失.而“一题多变性”变式是变式教学的基本策略之一，将其应用于高三数学复习课中，实现了“不变”与“变”的有机结合，促使学生多个角度理解问题，多个方面揭示问题本质，有助于加强学生对数学知识的理解，在潜移默化的过程中培养学生的数学思维.

一、“一题多变性”变式

“一题多变性”变式就是指，在教师的引导与指导下，改变数学问题的条件和结论，交换条件和结论或者增加延伸问题的条件，加深结论，其目的就是为了从多角度、多方面去揭示问题的本质.对于高三数学复习课来讲，采用“一题多变性”变式教学，就是依据一个典型的数学例题，通过“变”，最大限度地覆盖知识点，实现“以点带线，以线带面”的目标，这样既有助于帮助学生理解和掌握知识，完善学生大脑中的知识结构，更能够为学生提供一个训练思维的平台，促使学生的数学思维能力得到培养.高中阶段的数学课程可以分为代数与几何两大部分，而“一题多变性”变式在几何类问题中应用的方法大致为：条件、结论、逆向、开放性、综合性及引申性这六种变式，而其在代数类问题中的变式方法一般就是系数、指数、底数、项数、符号、字母、形式、问法以及题型这九种变式.

二、“四个”变式的原则

将变式教学应用于高三数学复习中，便于学生理解数学知识，也能够使学生从“变”中寻得“不变”，明确数学知识的本质特征.而要想真正发挥“一题多变性”变式教学在高三数学复习课教学中的优势，就要遵循相应的教学规律与原则，笔者通过查阅、分析文献资料，归纳了“一题多变性”变式要遵循的“四大”变式原则：

1.目标导向原则

高三数学复习课的特征就是内容多、综合性强，因此为了提高复习教学的质量，就要在课前做好充分的准备，制订明确、具体的教学目标，弄清楚哪些问题不用“变”？哪些问题需要“变”？需要“变”的问题，为何“变”？如何“变”？除此之外，作为一线教师，还应该明确课堂的时间有限，仅有45分钟，因此不能制订过多的目标，而是要抓住典型，深入挖掘，使学生举一反三.若课堂内容不分主次“讲”于学生，既不利于突出重点，也不利于攻克难点，进而导致复习教学的效果不甚理想.

2.难易适中原则

众所周知，任何事情都需要把握一个“度”，特别是对于师生皆为难度较大的数学学科来讲，在复习教学中，采用“一题多变性”变式教学，就要贯彻“以学生发展为本”的理念，遵循“难易适中”的原则，才能够取得预设的复习效果.对于“一题多变性”变式教学来讲，“难易适中”原则主要可以从两个方面进行理解，具体为：一是题量适中，在复习课堂上，出现变式题的数量要适中，不宜过多，也不宜过少；二是层层递进，把握好问题变式之间的难度与广度.

3.主体参与原则

学生是课堂教学的主体，对于复习课来讲也不例外，因此在采用“一题多变性”变式教学时，要贯彻“以生为本”的理念，认识到“变”并非是教师的“专利”，同时在“变”的过程中，教师不能仅顾自己“变”，而是要给予学生充分的时间与空间，让学生跟上教师“变”的脚步，更要鼓励学生积极主动地“变”，让学生敢于质疑，大胆发言.这样一来，既能够建立互相尊重、平等和谐的师生关系，还有助于学生认识到自身学习的主观能动性，进而使学生在参与的过程中提升自身的综合能力.

4.有针对性原则

“变”需要学生拥有扎实的基础知识，但由于学生的个性差异，每位学生的基础并不相同，所以在开展变式教学时，要结合学生的实际情况，开展有针对性的“变”，否则就会适得其反.若学生的认知能力与思维能力较高，那么教师可以适当地加大“变”的深度与广度；反之，教师就应该以基础知识为主，适当地降低“变”的深度与广度.笼统来讲就是，“变”要尊重学生的个性差异，因材施教，确保每位学生都能够获得发展.

三、“一题多变性”变式在“求圆锥曲线的离心率”中的应用

采用“一题多变性”变式教学，能够活跃课堂的教学氛围，吸引学生主动参与，同时也能够放飞学生的思维，使学生积极主动地思考探索，有效避免了死板与僵化，更重要的是，使学生在“变”的过程中，优化、完善大脑中的知识结构.在复习“圆锥曲线的离心率”的课堂上，笔者首先引导学生回顾了椭圆、双曲线及抛物线的几何性质，使学生的大脑中呈现出离心率的公式，加以点拨认知离心率的取值范围.而为了使学生掌握“求圆锥曲线的离心率”的技能，笔者结合一道实例，采用“一题多变”的方式，加深了学生对圆锥曲线的离心率相关知识的认知，同时也促使学生掌握了解题技巧，更使学生的思维得到了训练与提升.

例题已知椭圆C1的方程式为而椭圆C2过椭圆C1的两个焦点、短轴的两个端点，那么椭圆C2的离心率为______.

解析：由已知条件可知：

椭圆C1的两个焦点的坐标分别为0），短轴的两个端点的坐标为（0，3）、（0，-3）.

注释：通过题目的已知条件，就可以轻轻松松求得a与c，基于此，通过椭圆的离心率公式e就可以求得答案.该类型题目就是一道基础题.然而，在近几年的高考试卷中，有关离心率的题目，往往是不能够直接求得a与c的值，因此在课堂上，笔者并未到此为止，而是通过“变”的方式，进行了深入挖掘，使学生真正掌握了“离心率”这一知识点.

变式一：若双曲线的方程为（a>0，b>0），该双曲线的一条渐近线过点A（3，-4），那么该双曲线的离心率e为______.

注释：本题目，通过已知条件根本不能求得a与c的值，而我们可以结合已知条件给出的等量关系，列出a与c的等量关系，进而经过“变”得到此，结合离心率的公式，求得离心率该类题目的难度属于中等，在课堂上，教师要以引导、点拨为主，促使学生积极主动地“思”，同时还要及时关注学生的动态，80%的学生能够正确掌握该类题目的解题技巧.

变式二：已知F1、F2是双曲线的左右两个焦点，且F1、F2的坐标分别为（-c，0）、（c，0）.P是双曲线上的任意一点，且的最小值的取值范那么该双曲线的离心率的取值范围是______.

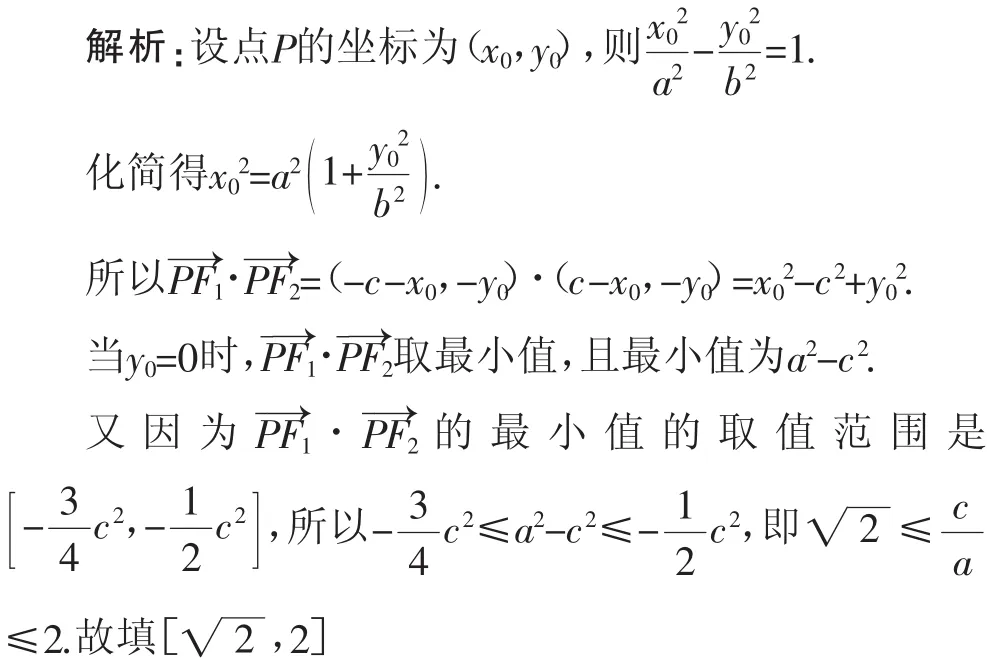
注释：该题目是一道综合性较强的题目，其中运用了向量的相关知识，难度也增加了，因此在课堂上，笔者要进行引导，但并非作为重点进行“讲”解，因为本题目的难度较大.