三角恒等变换综合演练A 卷

■刘中亮

一、选择题

1.若θ是第二象限角，且则

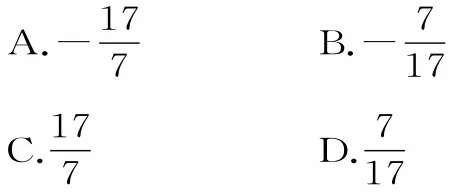
2.（较难题）已知α，β均为锐角，cos（α+，则（ ）。

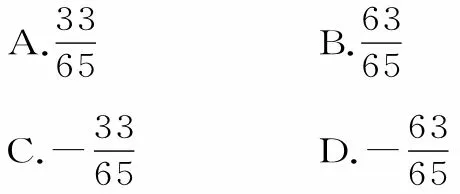
3.sin 15°+cos 15°的值为（ ）。

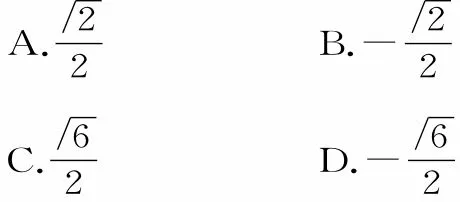
A.1 B.2

C.4 D.3

5.cos275°+cos215°+cos 75°·cos 15°的值是（ ）。

6.已 知x∈ （0，π），则tanx等于（ ）。

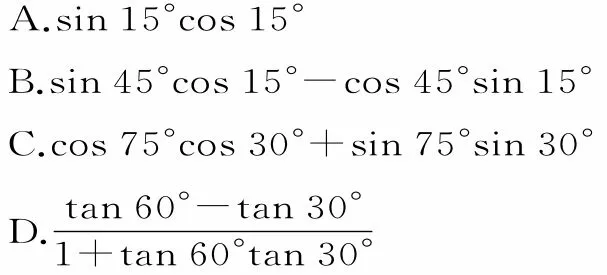
A.b＞a＞cB.a＞b＞c

C.a＞c＞bD.c＞b＞a

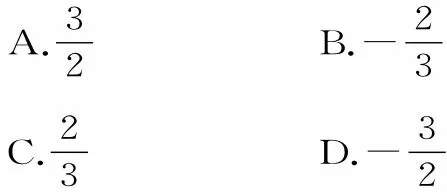
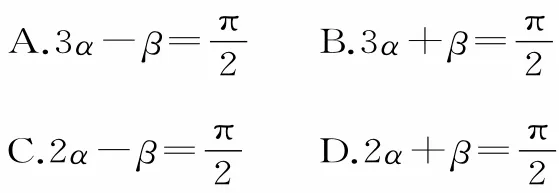
12.设α，β为钝角，且，则α+β的值为（ ）。

13.在北京召开的国际数学家大会的会标如图1所示，它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形，若直角三角形中较小的锐角为θ，大正方形的面积是1，小正方形的面积是，则 sin2θcos2θ的值等于（ ）。

图1

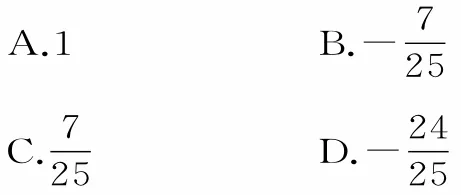
14.cos80°cos200°+sin80°sin200°=（ ）。

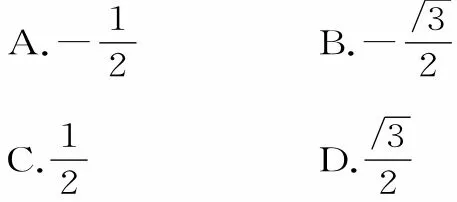
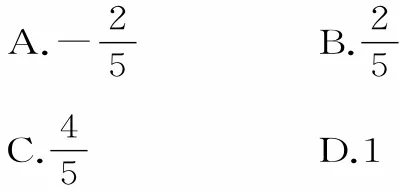
17.已知cos2α=sinα，则（ ）。

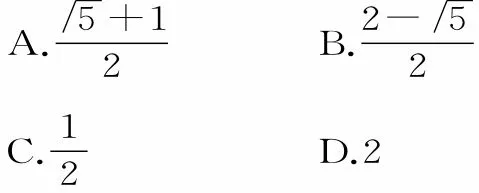
18.已知α满足，则

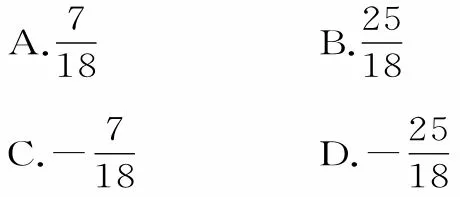
19.已知α，β为锐角，且，则cos 2β=（ ）。

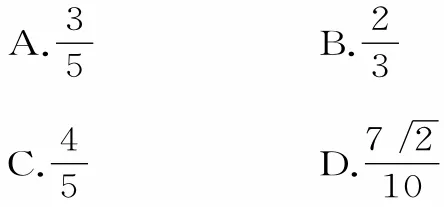
20.已 知 3 π≤θ≤4 π，且，则θ=（ ）。

存在多重共线性时，模型结果与实际情况不尽相符。为消除模型的多重共线性，本文采用岭回归方法进行回归数据有偏估计。京津冀、长三角和珠三角城市群模型岭迹见图4。由图4可得，京津冀城市群模型岭回归中，当参数k=0.2时，模型回归系数趋于稳定;长三角城市群模型岭回归中，参数k=0.12时，回归系数趋于稳定;珠三角城市群模型岭回归中，参数k=0.08时，回归系数趋于稳定。

23.已知tanB=2 tanA，且cosAsinB=，则

24.已知α为第二象限角，则的值为（ ）。

A.32 B.16

C.8 D.4

二、填空题

26.已知点P（3 cosθ，sinθ）在直线l：x+3y=1上，则sin 2θ=____。

27.sin135°cos（-15°）+cos 225°sin15°=____。

29.若关于x的方程sinx+cosx-m=0在区间上有解，则实数m的取值范围是____。

31.设当x=θ时，函数f（x）=sinx-取得最大值，则cosθ=____。

34.已知α为锐角，且=1，则α=____。

三、解答题

36.已知角α的终边上有一点P（1，2）。

37.已知函数f x（）=sinω xcosω x-的图像的两条相邻对称轴之间的距离为

（1）求函数y=f x（）的对称轴方程。

38.已知函数f（x）=cos2x+cos2（x+α）+cos2（x+β），其中α，β为常数，且满足0≤α＜β≤π。

对于任意实数x，问是否存在α，β，使得f（x）是与x无关的定值。若存在，求出α，β的值；若不存在，请说明理由。

（1）求函数f x（）的最小正周期和单调增区间。

40.如图2，以坐标原点O为圆心的单位圆与x轴正半轴相交于点A，点B和点P在单位圆上，且点

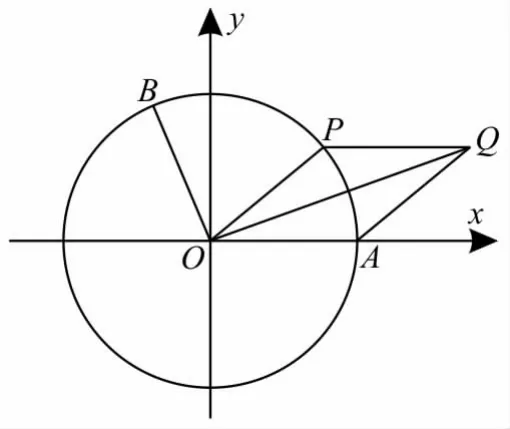
图2