三角函数求值与化简的三种常用方法

■张子璇

三角函数是高中数学的重要内容，三角函数的求值与化简是高考的常考点。三角函数求值与化简的三种常用方法是：弦切互化法，和积转换法和巧用“1”的变换法。下面举例分析，供大家学习与参考。

一、弦切互化法

例1已知tan（2019 π+α）=2，则

解：因为tan（2019 π+α）=2，所以tanα=2。故原式

评析：把转化成只含tanα的式子是解答本题的关键。

例2若tanα=2，则=____。

解法1：（切化弦的方法）因为tanα=2，所以sinα=2 cosα，即cosα因为sin2α+cos2α=1，所以

解法2：（弦化切的方法）原式=

评析：利用可以实现角α的弦切互化。

二、和积转换法

例3已知0＜θ＜π，且sinθ+cosθ=，则sinθ-cosθ的值为____。

解：由可得（sinθ+，所以。因为0＜θ＜π，且sinθcosθ＜0，所以sinθ＞0，cosθ＜0，可得sinθ-cosθ＞0。

又（sinθ-cosθ）2=1-2 sinθ·所以

评析：由sinθ+cosθ求出sinθ·cosθ是解题的突破口。

三、巧用“1”的变换法

例4已知则

解：

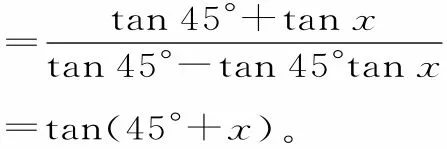
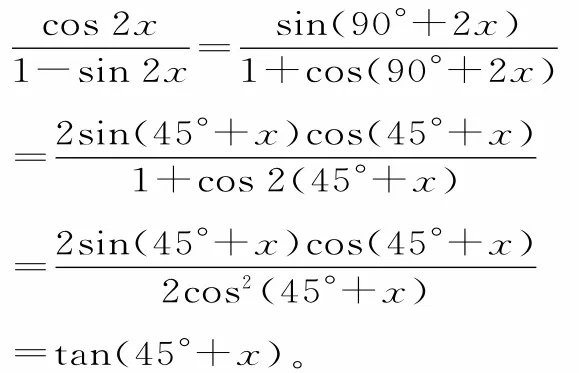
评析：由已知条件直接求出tanx，再求出的值，这种解题思路虽然直观但运算过程复杂。若利用进行替换，可使解题过程简洁流畅。

例5化简

解：易知sin 1＞cos 1。

评析：利用1=sin21+cos21，把根号里的式子化为完全平方式是解答本题的关键。