基于统计信息的多体系统区间不确定性分析

陈光宋，钱林方，王明明，林 通

(南京理工大学 机械工程学院，南京 210094)

多体系统动力学被广泛应用于机构、机器人、车辆及机床等机械系统，这些系统通过连接副和力元将多个零部件连接成有机的整体。尽管关于多体系统动力学的建模方法已经相对成熟，但是大多数的研究都假定系统内所有参数均为确定性的。然而，现实中由于载荷、几何尺寸、材料属性、制造和装配过程以及使用中的磨损等因素使得参数具有不确定性，这些参数的不确定性可能导致系统性能的显著变化。因此，研究含不确定性参数的多体系统动力学问题对确保机械系统的安全，提高系统的可靠性和稳健性等有重要意义。目前，处理不确定性问题的方法主要包括概率方法[1-4]、模糊集方法[5-7]和区间方法[8-10]。概率方法和模糊方法所需的概率分布信息和模糊隶属度函数在实际过程中不易获取，需要大量的试验，甚至无法准确获取。相反，区间方法所需的信息只是不确定性参数的上下界限，这两个参数获得的难度小很多，使用起来也更灵活和方便。然而，区间方法的问题是由“包裹效应”引起的区间扩大效应，如果无法有效控制区间的扩大，则这种方法将无法适用。Moore[11]对区间算法中用到的自然扩张函数、中心扩张函数和Taylor扩张函数进行了比较，其中Taylor扩张函数得到的区间最窄。

动力学问题的数学模型通常为强非线性的微分方程，解算过程需要采用较小的步长，将区间方法用于微分方程求解时，其“包裹效应”将更加显明，随着求解时间的增加，区间方法很可能导致求解发散，因此如何控制动力学问题的区间扩大问题，是区间方法在动力学问题中应用的关键。目前，国内外学者提出了许多方案来控制区间的过估计问题，例如区间泰勒级数方法[12]，泰勒模型方法[13]以及近年来由吴景铼提出的切比雪夫扩张函数方法[14-16]等，这些方法能够在一定程度上控制区间方法处理动态不确定性问题的过估计问题。其中泰勒展开的方法是侵入式的方法，需要修改动力学方程，而且多数仅能处理区间较小的情况，其他非侵入的方法在处理高维问题时会遇到计算量大等问题[17]。

本文提出一种区间方法用于解决含不确定性参数的动力学问题，利用极大极小距离的拉丁超立方采样(Latin Hypercube Sampling,LHS)方法获得样本点，根据样本信息统计获得响应的前四阶统计矩，并通过Bootstrap方法提高矩的计算精度，进而利用极大熵方法获得响应的概率密度函数和累积概率函数，将累积概率密度函数在样本极大极小点处进行泰勒展开，并令分布函数在估计区间的上界和下界上的值为1和0，反求出输出参数区间的上下界。最后，通过两个解析函数验证本文方法的收敛性，通过两个标准的机械系统动力学问题验证本文方法的有效性，通过一个工程算例验证本文方法的适用性。

1 机械系统不确定多体动力学控制方程

多体系统动力学控制方程通常为指标-3的微分代数方程组(Differential Algebraic Equations,DAEs)[18]，其中微分方程部分描述状态量对时间的导数，代数方程部分则是系统的完整约束条件。多体动力学系统的控制方程可写成如下形式[19]

(1)

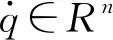
(2)

其中，

(3)

为了防止常用的积分算法在数值求解过程中的违约问题，Baumgarte[20]基于控制反馈策略提出了一种约束稳定方案

(4)

其中，

(5)

上述多体动力学控制方程为确定性的，考虑系统参数的不确定性，则控制方程变为不确定性控制方程

(6)

式中：x为不确定性参数。

为表述方便，考虑单个不确定性变量x，采用区间方法刻画不确定性参数，则参数x的区间可定义为

(7)

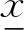
定义区间[x]的区间中点xc、区间半径xr和区间宽度xw为

(8)

(9)

xw=2xr

(10)

中心化的区间可表示为

[Δx]=[-xr,xr]

(11)

则真实的区间[x]可重写为如下形式

[x]=xc+[Δx]

(12)

2 基于统计信息的区间分析方法

2.1 极大极小距离的LHS

LHS具有非常灵活的特征，然而设计点的分布是任意的，不能很好的充满设计空间，导致参数设计矩阵不能很好地代表设计空间。本文综合计算效率和适用的灵活性，基于极大极小距离准则，采用近似优化的方案，获得较好的样本点。

定义多维空间中两点a和b的欧氏距离d为

(13)

式中：p为维度；d越小表示多维空间中点a和b越靠近。

为使设计点在空间中均匀分布，可通过使多维空间中距离最小的两个点a和b的距离最大来实现。实现的方法可分为优化方法和准优化方法。优化方法在维度p和样本点数N较大的情况下，计算量将非常大，实际上可采用近似均匀的策略，通过准优化的方法获得较均匀的样本，实现步骤如下[21]：

步骤1令I=mN，一般m=5，N为需要生成随机矩阵的行数，在[0,1]区间上产生I×p的均匀随机数，构成随机矩阵Rd；

步骤2对I中的第i行元素，计算欧氏距离dij，j∈1,2,…,I,i≠j，取出其中距离最小的两个并取平均值；

步骤3存储第i行元素的最小平均距离，i=i+1，返回步骤2，直到i=I；

步骤4删除平均距离最小的一组数据，因此I=I-1；

步骤5i=I，返回步骤2，直到I=N，形成均匀随机数矩阵R；

步骤6根据矩阵R，结合输入参数的区间范围，产生最终输入参数的设计矩阵D。

2.2 各阶统计矩的Bootstrap求解方法

将设计矩阵D中的输入参数代入多体系统动力学方程，通过解算获得输出参数样本Y，则样本Y的前四阶统计矩为：

样本均值

(14)

样本方差

(15)

样本偏度系数

(16)

样本峰度系数

(17)

通常在样本数量较多时，通过式(14)～式(17)可获得较准确的解，然而在样本数量较少时，对低阶统计矩的计算较准确，对高阶统计矩的估算可能产生较大的误差。为此，本文通过Bootstrap重采样方法来减小各阶统计矩估算的偏差。根据初始获得的样本，采用有放回的抽样方法，获得B组Boostrap样本，继而根据式(14)～式(17)计算获得每组Bootstrap样本的各阶统计矩，并取均值获得最终输出参数的统计矩

(18)

(19)

(20)

(21)

2.3 参数分布的极大熵估计

最大熵原理[22]可以描述为在给定的条件下，在所有可能的分布中存在一个使信息熵取极大值的分布，该分布是最小偏见的，由此可以得到一种构造最佳分布的方法。输出参数Y的信息熵为

(22)

式中：fY(y)为Y的概率密度函数；H为信息熵；Ω为积分空间。

假定fY(y)为如下形式

(23)

式中：ai为待定系数。我们的目标是寻找到一个分布函数(即一组系数ai)使得信息熵的值最大，并将随机变量Y的前四阶统计矩作为约束条件，可建立优化模型如下

(24)

基于梯度的优化方法能够得到较高精度的解，初值的选择对优化求解的收敛性有很大影响。采用基于正态分布的初始点则能更快更准确地搜索到最大熵对应的系数，初始点可设置为

(25)

通过求解上述优化问题，可得系数ai(i=1,2,3,4)，进而确定概率密度函数fY(y)，通过对fY(y)进行积分可得随机变量Y的分布函数FY(y)为

(26)

由概率密度函数的定义可知，FY(y)∈[0,1]，并且FY(y)单调递增，FY(y)的导数即为fY(y)，且fY(y)始终为正，这些性质是本文求解参数区间的基本保证。

2.4 基于泰勒展开的参数区间估计

假定ymin和ymax分别为“2.1”节和“2.2”节中通过极大极小距离LHS得到的有限样本的极小值和极大值。根据“2.3”节获得的累积概率密度函数FY(y)，在ymin和ymax处对其进行一阶泰勒展开，可得

(27)

(28)

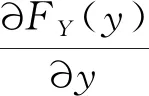
(29)

(30)

(31)

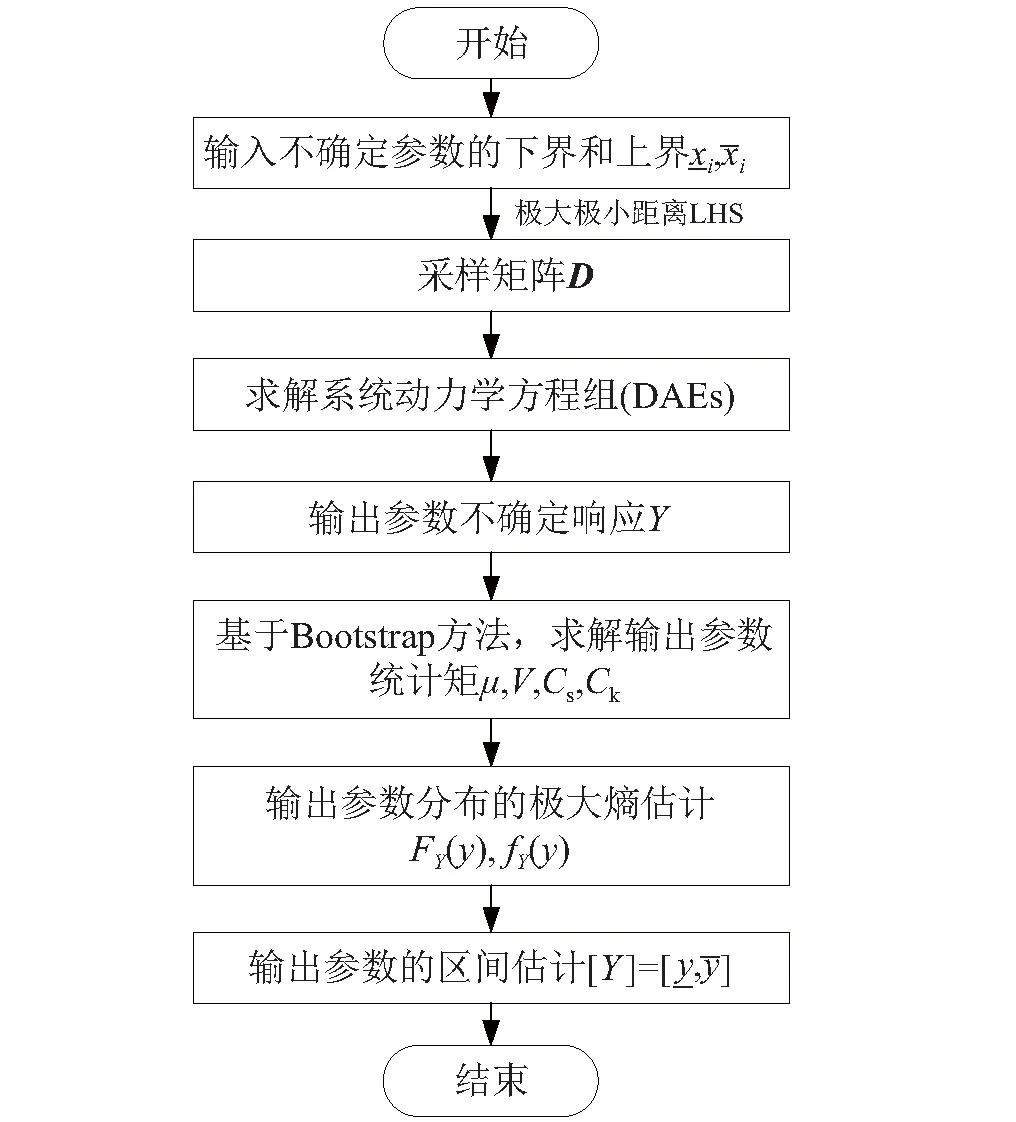
图1 计算流程图Fig.1 Flowchart of computation process

3 算 例

首先通过两个解析函数算例验证本文方法的收敛性，然后通过两个典型的多体机械系统(双摆机构和曲柄滑块机构)来验证本文提出区间分析方法的有效性，最后将本文方法应用于一个工程算例。

3.1 解析算例

考虑解析函数表达式如下

(32)

y2=-sinx1-2(sinx2)2

(33)

式中：x1∈[-π,π]，x2∈[-π/2,π/2]，输出参数在输入参数定义域内的曲线和曲面如图2(a)和图2(b)所示，其中输出参数的上下界均可通过优化的方法获得。为验证本文方法的收敛特性，在输入参数空间内分别采样20，40，60，80和100个样本点，计算输出参数上下界如图3(a)和图3(b)所示。点划线为本文计算出的上下界，虚线为通过优化方法获得的上下界。中间过程的各阶统计矩，如表1和表2所示。

图2 解析函数Fig.2 The analytical function

表1 函数1参数统计矩Tab.1 The statistical moment of the output of funtion 1

图3 不同采样点下的区间Fig.3 The interval evaluated by different number of samples

表2 函数2参数统计矩Tab.2 The statistical moment of the output of funtion 2

从图3可知，本文方法不仅可获得较紧的包含输出响应的区间，而且在较少样本的情况下也能获得较好的解，具有很好的收敛性。

3.2 双摆机构

双摆机构示意图如图4所示。其动力学方程为典型的多体动力学模型。参照Wu等研究中的参数，两根杆的长度分别为l1=l2=1 m，质心分别为O1和O2，质量分别为m1=m2=1 kg，重力加速度为9.8 m/s2。

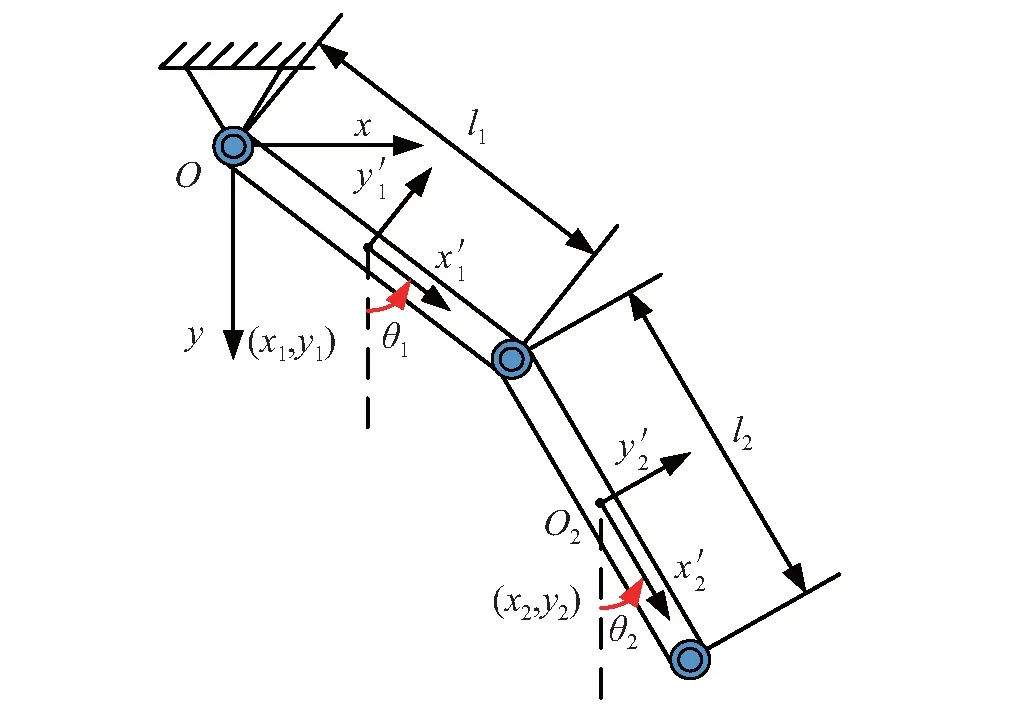
图4 双摆机构Fig.4 Schematic of the double pendulum

(34)

式中：

(35)

式中：diag([])为对角矩阵，对角元素为[]；惯性矩

(36)

考虑两杆长均为不确定性参数，其变化范围为名义值的5%，则有

(37)

式中：ξ1,ξ2∈[-1,1]，相应的质量和惯量矩也为不确定性参数，可表示为

(38)

(39)

通过四阶龙哥库塔法解算动力学方程，步长为0.001 s，采用本文的方法和优化方法计算从0～10 s时间段内两杆的质心位置，本文方法的样本点数取为100，为更有效地对比计算结果增加了区间中点以及任意一组确定性参数的响应值。计算结果如图5～图8所示。

图5 杆1质心水平位置Fig.5 Horizontal displacement of the top rod center

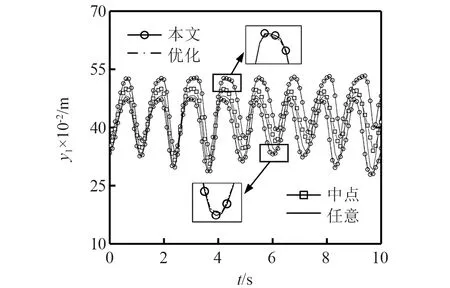
图6 杆1质心垂直位置Fig.6 Vertical displacement of the top rod center

图7 杆2质心水平位置Fig.7 Horizontal displacement of the bottom rod center

图8 杆2质心垂直位置Fig.8 Vertical displacement of the bottom rod center

从图5～图8可知，本文方法所求区间能够较好地包含优化方法获得的结果，且能够长期抑制区间过估计问题，从推导过程可知，与传统区间方法不同，本文所提出的方法无导致区间放大的区间运算过程，可避免区间的“包裹效应”，其区间估计的准确程度仅取决于估计输出参数统计矩所需样本点的数量，不会随着输入参数个数的增加而大幅增加。

3.3 曲柄滑块

曲柄滑块机构示意图如图9所示。图9中A点、B点和C点分别为曲柄、连杆和滑块的质心。Oxy为惯性坐标系，局部坐标系O1x1y1，O2x2y2和O3x3y3与3个构件质心固接，θ1和θ2为曲柄和连杆的转动角。在O点处施加一转矩τ，滑块末端与弹簧阻尼机构相连，刚度为k，阻尼为c。当θ1和θ2为0时，该弹簧处于平衡位置。图中l1和l2分别表示曲柄和连杆的长度，m1，m2和m3分别表示曲柄、连杆和滑块的质量，参照Wu等研究的参数，各参数取值如表3所示。

图9 曲柄滑块机构Fig.9 Schematic of slider crank

表3 曲柄滑块参数Tab.3 Parameters of slider crank

选择广义坐标q=[x1,y1,θ1,x2,y2,θ2,x3]T，则控制方程为

(40)

其中，

(41)

惯性矩为

(42)

考虑曲柄长度存在不确定性，其不确定范围为名义值的1%，即

(43)

质量和惯性矩的不确定性可表示为

(44)

考虑力矩τ在其名义值附近有1%的不确定性，即

(45)

初始条件如下

(46)

通过四阶龙哥库塔法解算动力学方程，步长为0.001 s，采用本文的方法和优化方法计算从0～2 s时间段内的响应，本文方法的样本点数取为200，并增加了区间中点以及任意一组确定性参数的响应值作为比较。计算结果如图10～图12，结果显示本文所得的结果能够完全包含实际解，即使在多个周期的往复运动后，估计的区间依然可靠，并且区间的放大现象得到很好的抑制。

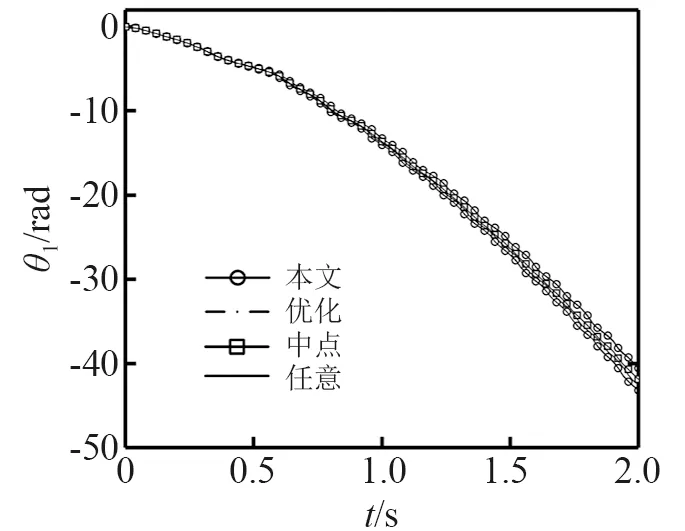
图10 曲柄转角Fig.10 Rotation angle of crank

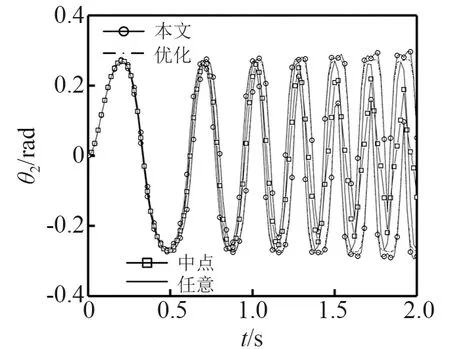
图11 连杆转角Fig.11 Rotation angle of connecting rod

图12 滑块位置Fig.12 Displacement of piston

3.4 火炮摇架俯仰运动

某大口径火炮上装部分示意图，如图13所示。其主要部件包括身管、摇架、上架、反后坐装置、炮尾等，火炮的高低射角通过高平机液压油缸的伸缩实现，此处为分析问题方便，假定在火炮发射过程中上架固定。由于高平机液压油缸受温度、容气量等的影响，使得火炮每次发射过程，摇架运动规律不一，对于长身管而言，摇架俯仰运动情况能够间接反映炮口扰动情况，虽无指标要求，但在火炮设计过程中，通常需要通过动力学模型进行检验，在射击精度试验时，也需要测试摇架的运动情况。因此，基于本文中的区间方法，对火炮发射过程摇架的运动进行不确定性分析。

图13 火炮上装部分Fig.13 The upper part of howitzer

高平机油缸示意图如图14所示，其中C腔与蓄能器相连，A腔和B腔为工作腔，初始压强分别为PA和PB，初始液压油体积分别为VA和VB，工作面积分别为

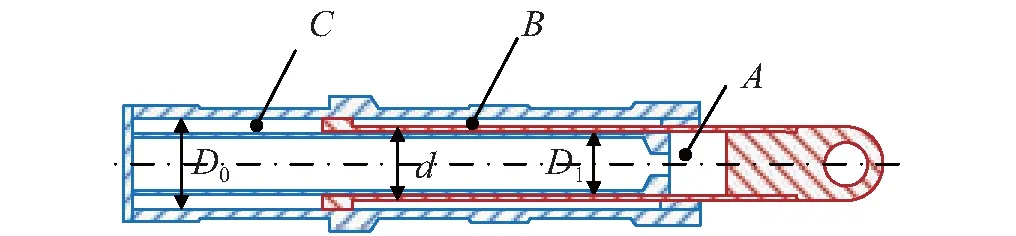
图14 高平机液压缸Fig.14 The hydraulic cylinder of elevating-equilibrium mechanism

(47)

(48)

液压油体积模量定义为

(49)

式中：Eh为不确定性参数，受温度和含气量影响，这里取值范围用区间表示为

(50)

(51)

另外还需考虑结构参数D1，d，D2以及液压油体积的误差，即

(52)

(53)

(54)

(55)

(56)

由此得到A和B腔液压油等效刚度分别为

(57)

(58)

则高平机的力学模型为

(59)

(60)

图15 摇架俯仰角速度Fig.15 The rotation angle of cradle

由图15可知，在火炮发射过程中摇架发生了周期性运动，而且考虑高平机参数不确定性的情况下，摇架的运动是动态不确定的，通过本文估计的区间能够较紧的包含优化方法得到的结果，说明即使在输入参数较多的情况下，本文方法仍能通过较少的样本点获得可靠的输出参数区间。

4 结 论

本文针对工程中多体系统的动态不确定性问题，提出了一种区间分析方法。该方法能有效避免由于区间方法固有的“包裹效应”导致的过估计问题，能够用较少的样本得到可靠的输出参数区间，且样本的数量对输入参数的数量不敏感。数值算例表明，本文方法对典型的机械系统动力学问题均有效，且能应用于复杂的工程实例。另外，值得注意的是：

(1)本文中计算输出参数的统计信息仅是为了获得输出参数区间而进行的数学处理手段，并非真实输出参数的统计信息，因此，本质上本文的方法还是一种利用统计信息的区间方法。

(2)采用本文的方法在样本数量很少的情况下，可能估计到的区间不能完全包含参数的真实区间，可通过增加样本数量解决，而且增加样本的过程不受区间估计算法的限制。