接触刚度对制动摩擦块时域-频域响应的影响
2019-06-13隋鑫,丁千,2
隋 鑫,丁 千,2
(1.天津大学 机械工程学院,天津 300350;2.天津市非线性动力学与控制重点实验室,天津 300350)
近年来,对摩擦耦合系统的失稳和制动尖叫的研究主要集中在黏滑自激振动机理和结构不稳定振动机理[1]。针对摩擦自激振动问题,刘丽兰等[2]介绍了机械系统中黏滑摩擦振动的研究情况;黄毅等[3]针对一类双质体-传输带干摩擦系统,分析內共振条件下的系统动力学现象;丁千等[4]总结机械系统中的摩擦模型与特性,对制动噪声、摩擦耗能等摩擦动力学研究进展进行综述;对于不同系统,摩擦力模型的选取将影响系统动力学特性的分析。
作为最典型的摩擦系统,车辆制动系统摩擦块与制动盘的耦合振动受到重视,分析模型和方法也很多。如Zhao等[5]采用伽辽金方法对刚柔耦合模型进行降维求解;Beloiu等[6]应用时域和频域的分析方法分析柔性耦合振动;李金录等[7]采用非光滑基函数方法,分析简化成局部约束梁模型的摩擦盘的模态;杨凤红等[8]建立两自由度非光滑动力学模型,研究制动盘转速对系统动力学行为影响。
由于摩擦块在制动盘的相对位置随时间变化,因此可以认为制动盘振动是受到移动载荷作用而产生的。YanmeniWayou等[9]通过模态分析方法,研究梁在移动载荷下的横向振动响应;李慧乐等[10]用有限元法,分析移动荷载作用下,简支梁结构的共振、消振机理;Chen等[11]采用多尺度法分析存在一定轴向速度的黏弹性梁的动态响应。移动载荷可能会激励出系统的多阶模态,而且模态的移动对相互的作用有一定影响。通过特征根分析也可以得到各阶模态的动力学失稳现象[12]。然而,采用移动载荷法对制动器摩擦动力学的研究还不多。Li等[13]建立柔性制动盘模型,研究移动载荷下的制动盘摩擦块分离、再接触问题。
针对摩擦块Stick-slip运动,接触表面的变化将影响系统的动力学响应。文献[14-15]的动力学模型均考虑了接触面的刚度特性;文献[16]指出,接触面的耦合刚度随表面的变形和磨损,及制动力大小的不同有所变化;文献[17-18]也提出,接触面变化对刚度和摩擦特性有影响。
目前,学者认识到接触面刚度的影响,但论文中仍缺少刚度变化对摩擦动力学影响的定量分析。据此,本文考虑摩擦块-制动盘耦合结构,研究接触刚度比的不同导致的动力学特性的变化,在数值计算中采用移动载荷法模拟盘-块的相互作用,分析摩擦块与制动盘接触刚度比对制动减速过程中的摩擦块动力失稳的影响。研究中发现的非完全黏滞现象与李博等的研究类似。
1 系统模型
研究图1中的摩擦块-制动盘耦合动力学系统。本文参数如表1所示。

表1 参数及取值Tab.1 Parameters and values
将摩擦块视为刚体,由牛顿定律推导其三个方向的运动微分方程为
(1)
而制动盘面外周向振动方程为
(2)
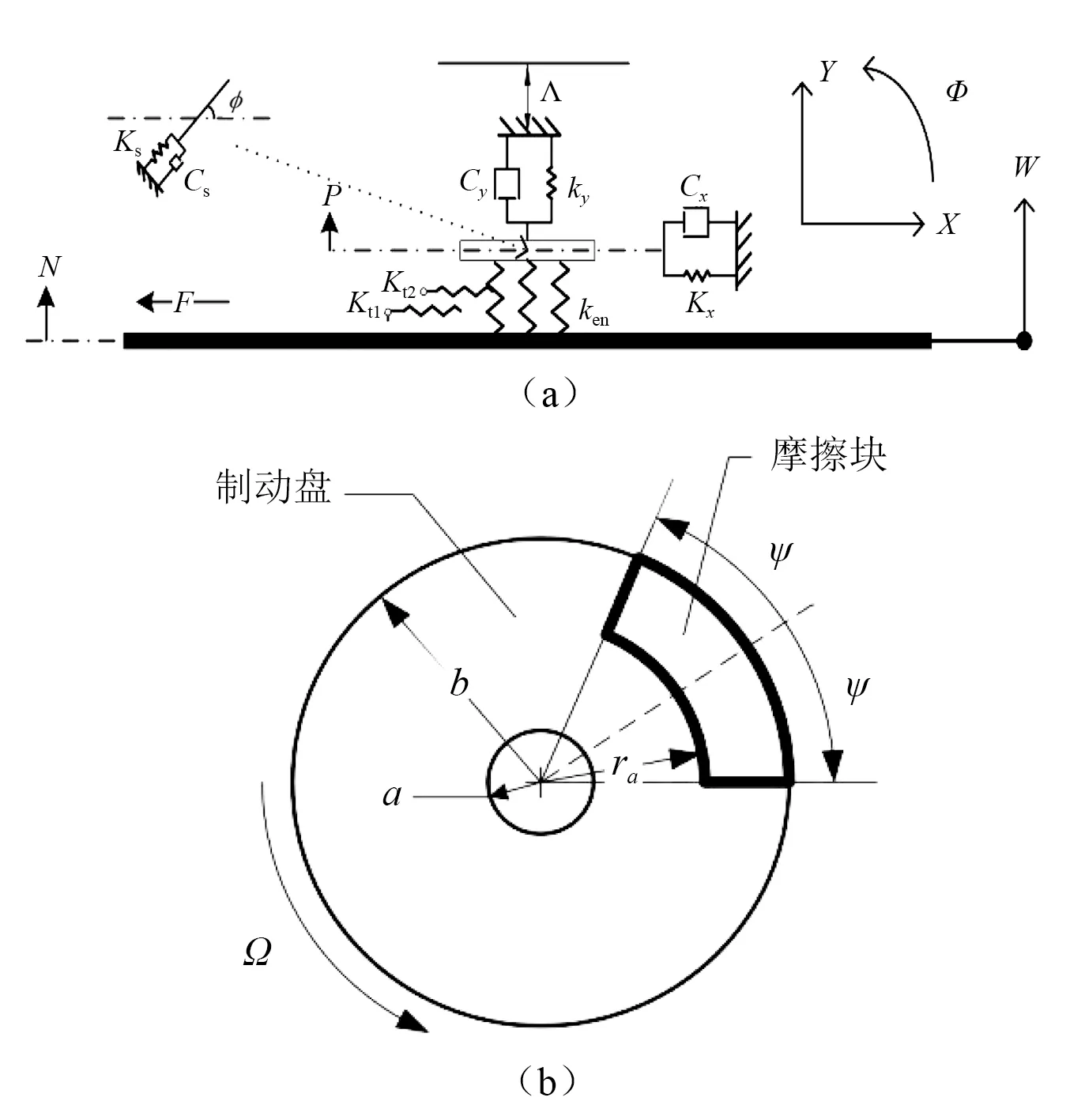
图1 摩擦块-制动盘耦合模型Fig.1 The model of pad-disc coupling system
(3)
式中:P,F分别为摩擦块受到的压力和摩擦力;Fc=(kt2X-αF)为制动盘与摩擦块接触范围的切向力合力。二者的相对位置实时变化且与速度Ω有关,可以写成σ=Ωt,V=RcΩ,Rc为摩擦合力作用点半径,则摩擦盘外缘线速度为Vouter=Ωb,α=kt2/kt1为摩擦块与制动盘之间的接触刚度比;αF为盘-块摩擦力产生的表面切向约束力。
采用差分法对摩擦盘进行求解,将接触力进行离散
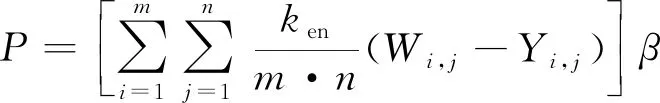
(4)
式中:i为制动盘径向第i个节点;m为总节点数;j为周向第j个节点;n为总节点数。
引入无量纲变量
(5)
将式(1)和式(2)无量纲化,得到
(6)
摩擦力分为静态摩擦力和动态摩擦力。根据所研究问题的不同,需要选择合适的摩擦力模型,如库伦摩擦、静摩擦、Stribeck模型等。
Stribeck效应是指在低速下摩擦因数先随速度增加而减小,然后上升,出现负斜率摩擦现象。考虑其Stribeck效应的摩擦力因数可以表达为
μ(v)=μssgn(vr)-k1vr+k3vr3
(7)
式中:μ(v)为摩擦因数;μm为最小动摩擦因数;μs为最大静摩擦因数;vm为最小动摩擦因数对应速度;vr为相对速度;如图2所示。

图2 Stribeck效应摩擦模型Fig.2 The model of Stribeck-type friction


图3 移动载荷分析Fig.3 Simulation of moving interactions
2 Hopf分岔
运动方程式(5)包含摩擦块振动常微分方程和制动盘振动偏微分方程。分别采用Runge-Kutta方法和有限差分法进行数值模拟,用移动载荷法处理其相互作用(压力和摩擦力)。本文主要分析摩擦块的水平运动。通过调节摩擦块与制动盘表面接触刚度比α,计算得到制动盘减速过程(称为速度正向变化)中的分岔类型,分岔图如图4所示。由于考虑制动盘在摩擦块持续作用下的面外振动,摩擦块的平衡始终受到其影响,称为相对平衡点。随着速度减小至某个临界速度(失稳点),摩擦块的稳定相对平衡点失稳,切向产生Hopf分岔。计算发现,尽管刚度比不同,在α=3.0~0.6,均产生超临界Hopf分岔。
α=3.0时,临界速度为2.94。摩擦块切向运动快速变为较大幅值的稳定极限环振动,直至速度减小至Ω=2.62。在速度为2.94~2.62,极限环是纯滑动的。随后,极限环幅值随着速度继续减小直至同时为零,在此期间的极限环包含了黏滞阶段,且速度越低,黏滞过程越明显。此外,图5相轨迹显示,摩擦块的黏滞过程为非完全黏滞,即速度并非为定值,而是仍有一定幅度的抖动,是造成摩擦高频振动的原因之一。
同样地,α=1.0时的临界速度为2.48,在Ω=2.48~2.18出现纯滑动;α=0.6时的临界速度为1.83,在Ω=1.83~1.64出现纯滑动。因此,临界转速随表面接触刚度比降低而减小,纯滑动范围也随之减小。摩擦块与制动盘表面并非光滑,在表面受力变形时,两者表面粗糙程度发生变化,刚度比反映表面变形时的相互约束情况,其比值与摩擦力项耦合,即α|F|。当表面粗糙度改变时,α对摩擦力有放大或缩小的作用。选取摩擦材料时,为避免非完全黏滞伴随的高频振动的出现,应选取刚度比较小的摩擦材料。制动器工作期间,尽量保持较低刚度比,即保证盘-块间的材料刚度与表面粗糙度适当,使得盘与块的约束充分。
3 极限环的频率特点
本节分析摩擦块水平振动极限环的频率特点。在图6、图7的低速(Ω=1.0时)的黏-滑振动中,均可见切向振动主导频率的存在,且刚度比较大时,伴随有多阶频率,频率成分相对明显。α=0.6(见图6(b))时,低速主导频率为0.333,高阶频率不明显;α=1.0(见图6(c))时,低速主导一阶频率为0.330,伴随有0.661,0.992等倍频,但高阶幅值相对较小;α=3.0(见图7(b))时,在频率1以内,主导一阶频率为0.308,并伴随有0.618,0.926等倍频成分。此时,表面的接触作用较弱,出现非完全黏滞过程,伴随有高阶频率成分。

图4 不同刚度比时的摩擦块切向分岔图Fig.4 Pad’s tangential bifurcation diagrams at different stiffness ratios

图5 不同转速下摩擦块切向相轨迹(α=3.0)Fig.5 Pad’s tangential phase portraits at different speeds(α=3.0)
通过以上分析,当表面接触刚度比较大时,非完全黏滞现象相对明显。α=3.0时,摩擦块切向位移随时间变化的图像呈现锯齿状,随着刚度比的增大,时间历程的曲线由圆滑逐渐变为锯齿形。摩擦块切向速度响应(见图7(c))中,黏滞部分出现抖动。可以看出,在制动盘转速相同时,刚度比的增加使得摩擦块切向速度随时间变化的幅值增大。

图6 不同刚度比摩擦块切向时间历程与频谱Fig.6 Pad’s tangential time histories and spectrums at different stiffness ratios
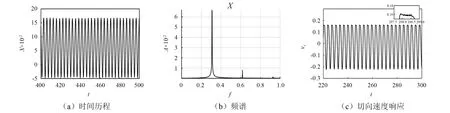
图7 摩擦块切向响应与频谱(α=3.0)Fig.7 Pad’s tangential response and spectrum(α=3.0)
4 结 论
本文建立了摩擦块-制动盘系统的刚柔耦合动力学模型,考虑移动载荷作用,应用Runge-Kutta法和有限差分法进行求解。研究表面接触刚度比对其Hopf分岔的影响,并分析移动摩擦块的时域-频域特性。结论如下:
(1)盘-块表面接触刚度比的不同导致摩擦块切向幅值对转速的Hopf分岔形式不同,且Hopf失稳点随刚度比的增加而增大;盘-块表面接触刚度比相对较大时,摩擦块切向出现非完全黏滞现象。
(2)非完全黏滞发生时,伴随有多阶频率;随着刚度比的增加,摩擦块切向振动主导频率降低,高阶幅值变大。
(3)相同转速下,非完全黏滞越明显,速度和位移随时间的振动幅值越大。
