基于弹塑性理论的落石碰撞恢复系数和峰值冲击力研究
2019-06-13梅雪峰胡卸文杜映锦马洪生吴建利
梅雪峰,胡卸文,2,罗 刚,杜映锦,马洪生,吴建利
(1.西南交通大学 地球科学与环境工程学院,成都 610031;2.西南交通大学 高速铁路运营安全空间信息技术国家地方联合工程实验室,成都 610031;3.四川省交通运输厅公路规划勘察设计研究院,成都 610041)
崩塌落石是高山峡谷区常见的斜坡地质灾害之一[1]。典型的落石过程一般要经历四个阶段:坠落启动-滚滑加速-抛射碰撞-减速停止(见图1)。岩土体间发生的复杂冲击和接触决定了落石的运动形态[2]。Ritchie[3]是第一个系统性研究落石问题的学者。Rochet[4]根据规模将落石分为2类:单体落石(1×10-2~1×102m3);落石群(>1×102m3)。其中,落石群又可分三种规模:一般、较大、超大。体积分别介于1×102~1×105m3,1×105~1×107m3及大于1×107m3。由于落石具有突发、随机及高能的动力特性,因此对生命、房建、交通及环境带来巨大的威胁。中国[5]、Nepal[6-8]、Italy[9-10]、Canada[11]、Japan[12]、Peruvian Andes[13]等地落石灾害均造成了巨大的损失。Gardner对Lake Louise地区842 h的调查,共报告了563起落石事件。
撞击过程中的峰值冲击力和恢复系数是落石问题研究中最主要的两个特征参量,其决定了落石的危害程度、影响防护结构设计特征参数及落石运动轨迹等。Asteriou等[14]采用试验研究了落石恢复系数与落石质量及冲击速度之间的关系。Labiouse等[15]分析了落石的回弹规律。Peila等[16]开展了大比例加筋土拦石墙结构模型的抗冲击性能试验研究,Ronco等[17]通过ABAQUS/Explicit有限元对Pelia等的研究进行数值模型验证。Asteriou等[18]基于室内试验提出了一种预测落石轨迹的三维经验模型。Chau等[19]研究了落石运动过程中与斜坡的锁闭效应。袁进科等[20]采用冲击力测试装置获取了不同质量、不同速度的落石对土石缓冲层结构的冲击力变化规律。杨海清等[21]基于Thornton模型推导了落石正面撞击地面的法向恢复系数。何思明[22]研究了典型正碰撞情况下落石对防护结构冲击力计算表达式。王东坡等[23]基于Olsson动力控制方程研究了落石冲击荷载作用下的棚洞顶板的动力响应。王爽等[24]采用模型试验研究了不同冲击能量下拱形棚洞结构的抗冲击性能。此外采用波动理论、数值模拟、基于概率论的不确定性评价也是研究落石问题的手段。
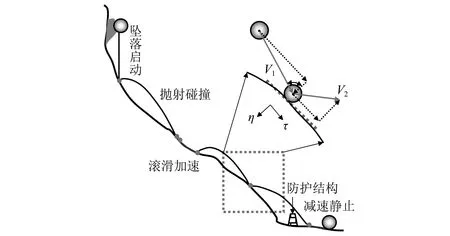
图1 落石运动过程示意图Fig.1 Movement process of Rockfall
作为弹塑性体,岩土体的塑性变形是撞击行为的主要控制阶段。法向塑性变形与切向摩擦是撞击过程中能量损失最主要组成部分,也是回弹恢复系数小于1的原因。基于Newton定义的运动学恢复系数是目前解决落石撞击问题的主要方式(回弹速度与入射速度之比)。一些学者在采用此种定义的恢复系数研究落石碰撞过程中发现回弹速度很大,甚至出现恢复系数大于1的能量不协调情形[25-26]。此外,通过试验反演恢复系数多采用中小尺寸模型[27],其试验材料尤其是滚滑面材料的力学物理特性与天然状态下差异较大,无法还原真实落石运动特性,实际碰撞过程中较小的落石受到坡面粗糙度的影响更显著[28]。而采用经验半经验所建议的法向和切向恢复系数差别非常大,导致选取及计算的困难。目前关于冲击力的计算方法多是忽略摩擦,基于正面碰撞下的经验半经验公式。而正碰仅是斜碰的特殊情况,实际过程中斜碰撞更为普遍,尤其是大角度斜碰撞过程中,摩擦作用非常明显,甚至成为主要控制因素,忽略摩擦可能导致恢复系数偏大。相对于滑坡、泥石流等地质灾害,落石灾害研究明显滞后,严重制约着合理有效防治措施的实施。针对上述问题,本文在经典接触理论的基础上,建立了一套相对完整的落石运动计算方法。提出了一种计算切向力的新模型,通过坡面条件及入射条件对可能掉落的危岩体进行运动形态的判别。采用算例与当前常用模型进行对比讨论,比较了模型之间的差异,验证了本文理论的合理性,对于预测和减轻落石灾害具有理论和现实意义。
1 落石碰撞过程机理
落石冲击地面的过程分为两个阶段:首先是开始接触发生压缩变形至变形量最大,此时落石速度为0,该阶段为压缩加载阶段;随后土体发生回弹直至落石与地面分离,速度达到最大,该阶段为回弹卸荷阶段。第一阶段速度逐渐减小,冲击力逐渐增加;第二阶段速度逐渐增加,冲击力逐渐减小。本文假设覆盖层为弹塑性体且在碰撞过程中忽略落石与长大树干间的相互作用。
1.1 弹性加载过程
根据Hertz接触理论[29],接触区应力分布函数为
(1)
(2)
(3)
接触域上的总荷载与压力的关系为

(4)

联立式(2)~式(4)得弹性阶段荷载与贯入量的关系
(5)
式中:Ei,Ej,Ri,Rj,vi,vj分别为落石和地面的弹性模量(Pa)、半径(m)、泊松比。
Jackson等[29]研究了弹塑性材料屈服应力与贯入深度间的关系
式中:δy为土体初始屈服时的贯入量,m;σy为土体的初始屈服应力,Pa,可依据试验或经验获取,且C=min(1.295e0.763vi,1.295e0.763vj)。
将式(6)代入式(5)得土体屈服压力
(7)
根据Jackson等[31],屈服时的最大变形能
(8)
将式(6)、式(7)代入式(8)得土体初始屈服时的速度
(9)
假设碰撞前质心的速度为V1,碰撞后速度为V2,任意时刻的速度为v,据功能原理
(10)
将式(5)代入式(10)得
(11)
当土体达到第一次屈服时土体的瞬时屈服速度
(12)
根据牛顿第二定律得
(13)
两边对δ积分得
(14)
(15)
将式(15)代入式(5)得到弹性阶段最大压力
(16)
1.2 塑性加载阶段
根据Johnson等的理论,开始发生塑性变形有以下关系式
p=ζσy
(17)
随着冲击力的增加,接触面积增大,接触区面积增量为:dA=2πrdr,因此有
dF(δ)=ζσy2πrdr
(18)
由式(17)、式(18)得塑性阶段荷载与贯入量的关系

(19)
对式(19)积分并联立式(3)得到屈服阶段荷载与贯入量的表达式
Fep(δ)=Fy+πσyR*(δm-δy)
(20)
式中:ζ为无量纲因子,Johnson等建议ζ=1,δm为任意时刻最大贯入量,m。
由功能原理得
(21)
根据式(21)可求得最大贯入量,代入式(20)可求得最大荷载Fepm。
1.3 回弹卸荷阶段
回弹卸荷阶段,荷载与贯入量仍然符合弹性理论
(22)
根据Kligerman等[32]的理论
(23)
由式(23)并根据动能定理得碰撞结束后落石的恢复能量
(24)
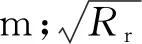
由初始碰撞时刻总的输入能量与式(24)联立,得到以输出与输入能量比值所表达的能量恢复系数
(25)
由式(25)可知,恢复系数与撞击过程中输入能量和输出能量相关。相比Thornton模型采用的速度恢复系数,本文基于能量原理推导的恢复系数表达形式较复杂,但系统性更强更符合实际。
2 切向冲击过程计算
2.1 切向冲击力
Mindlin[33]最早研究了接触体在固定法向荷载作用下,接触体表面切向力的分布规律。Vu-Quoc等[34]提出了不同荷载组合下弹塑性接触面的应力-应变模型(Thomas-Fexmi-Dirac,TFD)。何思明等[35]在Mindlin接触理论基础上推导了土体切向冲击过程,但是所假设的固定法向压力与实际情况不符。Fujimoto等[36]推导了塑性变形过程中,接触表面切向载荷与切向变形之间关系。考虑到落石撞击属于低速准静态碰撞问题,因此假设切向力近似等于摩擦力。目前关于切向力的计算方法,均采用Coulomb-Amontons摩擦定律(见图2)。Maw等[37]通过对斜撞击的研究表明,撞击过程切向力的变化是受冲击入射角的影响,并将斜碰撞过程分为:黏滞、黏滞-滑移、完全滑动三阶段。定义

(26)
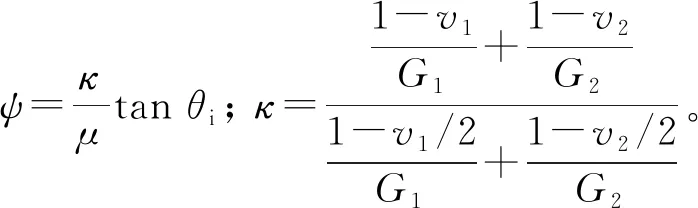
Maw等认为,考虑不同的撞击条件,当ψ≤1时,接触区之间无相对运动的趋势,在整个撞击过程中均为黏滞,而不存在微滑或滑动;当1<ψ≤4χ-1时,碰撞以完全滑动开始,并以完全滑动结束,其余为滑移与黏滞共存的过渡阶段,但是过渡阶段持续的过程极短,仅占整个冲击过程的不到2%;当ψ>4χ-1滑动发生在整个碰撞过程。考虑当满足1<ψ≤4χ-1时,接触面仍以滑移为主。本文在Coulomb-Amontons、Maw等的理论基础上提出一种新的切向力计算模型,表达式
(27)
式中:ψi为初始入射角(°);ψc为黏滞与滑动的临界摩擦角(°),本文计算中
对于给定的材料常数,根据以上公式可求得黏滞与滑动的阈值。由此可见,当θi→0时,ψi→0,此时切向力Fτ→0,为正碰撞;当θi→90°时,切向力Fτ=μFη,计算满足经典Coulomb-Amontons准则。
由图3可知,传统的摩擦力模型无法考虑不同运动状态下切向力分布特征以及切向力随冲击角度的变化规律,切向力在原点处梯度无限大且积分不连续。本文所提出的切向力计算模型很好的解决了以上问题,并且可以根据入射条件判别落石冲击过程中的运动形态,对于实际的工程应用简便有效。由图2可知,摩擦因数与土体临界摩擦角呈正相关。三维空间内,临界摩擦角是大小为2ψc的锥体,称为摩擦锥。本文所涉及的土体摩擦因数为0.4,其临界摩擦角等于24.5。

图2 摩擦因数与临界摩擦角Fig.2 Friction coefficient and critical friction angle

图3 切向力计算模型Fig.3 Tangential force calculation model
2.2 切向恢复系数
落石在碰撞过程中如果发生黏滞,则恢复系数为0。在滑动阶段,Kharaz等[38]提出了滑动阶段切向恢复系数的计算表达式
eτ=1-μcotθ(1+eη) 0≤eτ≤1
(28)
结合以上分析得落石冲击过程切向恢复系数的最终计算表达式
(29)
根据以上的理论,建立整个落石冲击过程中恢复系数(法向与切向恢复系数)、冲击力(法向与切向冲击力)之间的关系。
3 工程算例分析
已知坡面为残坡积覆盖层,参数见表1。采用本文理论讨论碰撞过程中不同特征参量对冲击力、恢复系数的变化规律。

表1 落石冲击计算材料参数[39]Tab.1 Rockfall impact calculation material parameters
3.1 恢复系数与速度的关系
为了研究落石速度与恢复系数的规律,在相同入射角情况下,以入射速度为自变量,计算得到了冲击过程中法向与切向恢复系数(见图4)。结果表明,当入射角为60°时。无论是Thornton模型抑或本文模型,法向恢复系数随入射速度增加而减小,而切向恢复系数随速度的增加而降低。其他条件相同的情况下,本文模型的法向恢复系数最大为0.28,而Thornton模型为0.42,与Thornton模型相比,本文推导的法向恢复系数值远小于相同速度下的Thornton模型。过大的恢复系数可能造成防护结构的失效及材料的浪费。此外,相同速度条件下,依据法向恢复系数计算得到的切向恢复系数对于两种模型相差不明显。本模型算例参数接近软土性质,陈洪凯等[40]建议的软土法向恢复系数为0.10~0.25,与本文计算结果较吻合,而Thornton模型偏离程度较大。

图4 速度与恢复系数的关系Fig.4 Relationship between velocity and coefficient of restitution
3.2 速度与冲击力的关系(见图5)
采用本文理论计算了落石碰撞过程中峰值冲击力随速度变化的规律(见图6)。结果表明,峰值冲击力随速度增加而呈线性增加的趋势,法向力增加的速率大于切向力增加的速率。与Labiouse等及Kawahara等[41]模型计算的冲击力对比发现,三种模型计算的冲击力增大趋势基本相同,但本文模型计算的冲击力略大于Labiouse模型,而远大于Kawahara模型,计算发现,在低速碰撞过程中,另外两种模型所得冲击力分别为0.99 t和0.64 t,其冲击力峰值均略小于自身重量,显然,两种模型存在着一定的误差。在高速撞击过程中本文结果与Labiouse模型较一致。
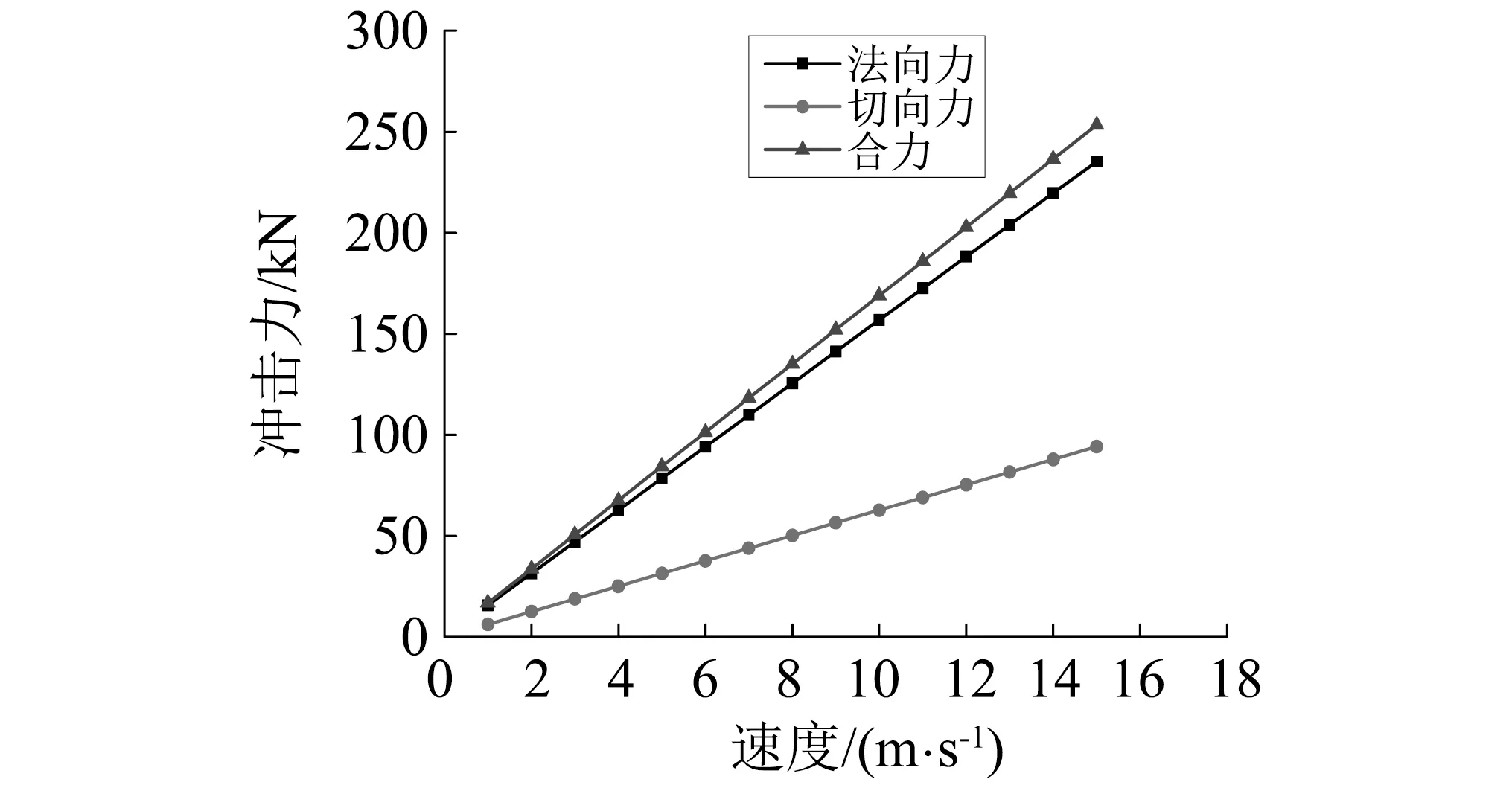
图5 速度与冲击力的关系Fig.5 Relationship between speed and impact force

图6 不同模型的峰值冲击力Fig.6 Peak impact force of different models
3.3 恢复系数与入射角的关系
以入射角(见图1)为自变量,研究了入射速度为15 m/s时恢复系数与入射角度的变化规律(见图7)。结果表明,撞击过程可分为黏滞阶段与滑动阶段,当入射角小于临界入射角时,切向恢复系数为0,法向恢复系数随入射角的增加而增大。当入射角大于临界入射角时,法向与切向恢复系数均随入射角的增加而增大,最大法向恢复系数为0.21。法向恢复系数的大小主要受控于入射速度的大小。入射角的改变对切向恢复系数的影响要远大于对法向恢复系数的影响。
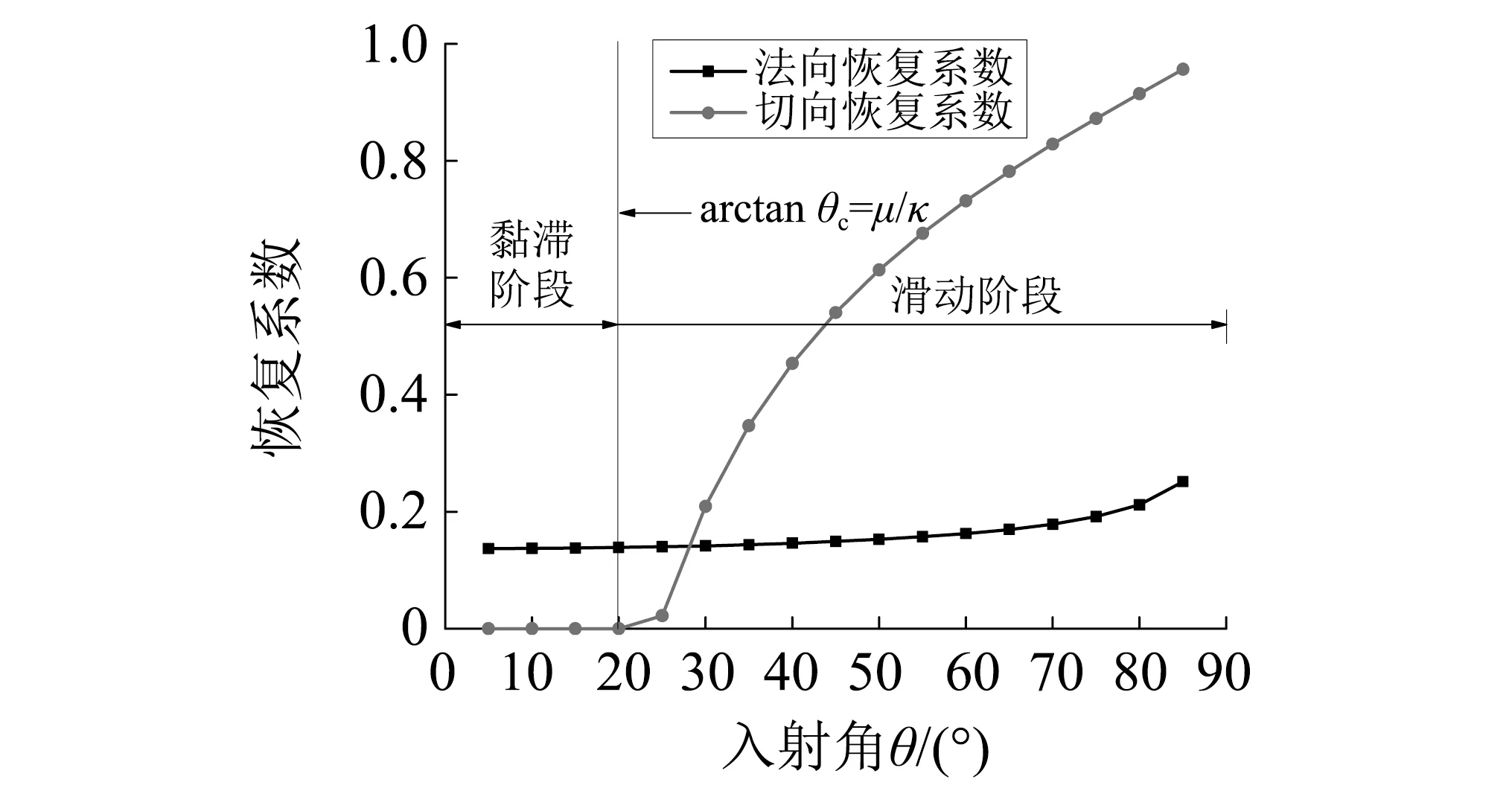
图7 入射角与恢复系数的关系Fig.7 Relationship between the incident angle and the recovery coefficient
入射角随冲击力变化规律(见图8)表明,碰撞过程中合力与法向冲击力随入射角的增加而减小,而切向冲击力在黏滞阶段随入射角的增大而增加,在其达到临界摩擦角时,切向力达到最大的78 kN,随后进入完全滑动阶段,在其他条件不变时,切向力随入射角的增大而减小。入射角与切向力的关系(见图9)表明,切向力与滑动摩擦力的比值分为两个阶段:第一阶段,两者比值与入射角成正比;第二阶段,比值为常数1。
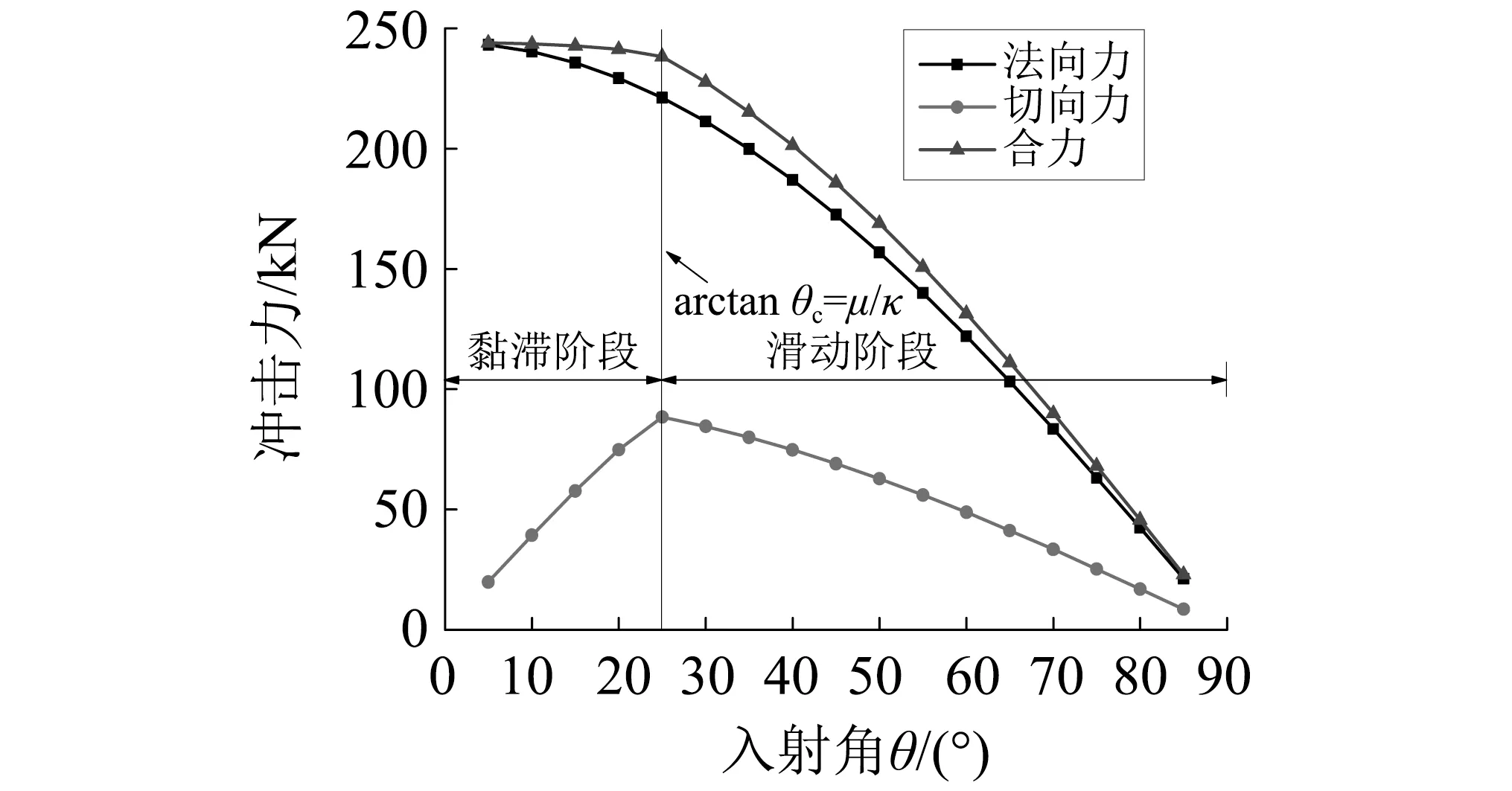
图8 入射角与冲击力的关系Fig.8 Relationship between incident angle and impact force
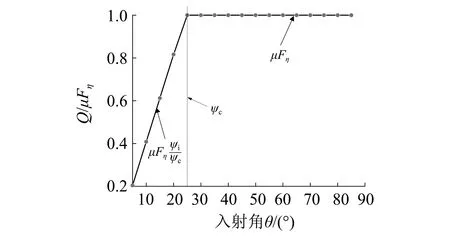
图9 入射角与切向力的关系Fig.9 Relationship between incident angle and tangential force
4 结 论
采用经典接触力学,推导了落石碰撞过程中的能量恢复系数和冲击力的计算公式。研究了以初始入射速度和入射角为变参量下的恢复系数和冲击力的变化规律,通过算例分析并与目前常用的计算模型进行比较,得到了以下结论:
(1)落石碰撞过程中法向恢复系数随速度的增大而增加,切向恢复系数反之。
(2)随入射角的增大,法向与切向恢复系数均有增加的趋势,且切向恢复系数增加的幅度远大于法向恢复系数。
(3)法向冲击力随速度增大而增加,随入射速度增加而减小。切向冲击力随速度增加而增加,随入射角的增加先增大后减小。
(4)通过实例验证并与目前采用的模型进行分析比较,表明,Thornton模型计算的牛顿恢复系数偏大,在实际应用中可能会造成防护结构的失效或材料的浪费。此外,采用Rockfall等软件进行落石运动模拟时,需自定义恢复系数,合理的恢复系数是正确预测落石轨迹、能量计算的关键。本文模型对落石碰撞过程恢复系数与峰值冲击力的计算更系统合理。
(5)落石回弹运动状态取决于初始入射条件。当入射角大于临界黏-滑入射角时,碰撞过程均存在滑动,反之落石发生黏滞。通过本文的模型也可判别落石撞击过程中运动状态的形态及其转化过程。
