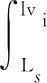超深矿井提升系统两绳区圈间过渡不同步时钢丝绳张力差分析

2019-06-13龚宪生宁显国

振动与冲击 2019年8期

张骁，龚宪生，宁显国，万园

(1.重庆大学机械传动国家重点实验室,重庆 400044；2.重庆大学机械工程学院,重庆 400044)

近年来，随着我国国民经济的快速发展，我国对矿产资源的需求量大幅增加，促使我国对地下矿产资源的开采不断向深层扩张，未来10年我国的采矿深度将达到1 000～2 000 m。由于单绳缠绕式提升机和摩擦式提升机，会随着采矿深度的增加，钢丝绳直径和尾绳重量都会急剧增加，因此不能满足超深井提升的需求[1]。因此，多点并行驱动的多层缠绕式提升机有望成为深部矿产资源开发的有效提升装备，其具体结构形式如图1所示。

与传统的提升机不同，每一个卷筒上有两个缠绳区，两根钢丝绳绕过天轮分别与容器相连，并将其重量均匀分配到两根钢丝绳上，从而实现高速的同步提升。超深矿井提升装备的重负载、高速度、大惯量和钢丝绳在高速缠绕过程产生的周期扰动、缠绕误差等会引起多点驱动柔性系统的变形失谐。变形失谐会导致两根钢丝绳长度出现差异和缠绕不同步，造成钢丝绳的张力异常，引起两钢丝绳之间的张力差过大，导致钢丝绳的寿命急剧缩短，甚至引发钢丝绳张力超标、断绳等重大安全事故。因此对提升系统钢丝绳在多绳多层缠绕下特别是对超深井提升，其振动特性将更加复杂，建立更加符合实际提升系统钢丝绳的动力学模型和研究其动力学特性十分重要。

图1 双绳多层缠绕式提升系统Fig.1 Diagram of the ultra-deep mine hoisting system

目前，国内外学者对电梯和摩擦式提升系统钢丝绳振动特性进行了一定的研究。王春华[2]利用集中质量法建立了塔式多绳摩擦提升系统的横向振动模型，发现绳长变化比重锤质量变化对提升钢丝绳固有频率影响更大；张长友[3]建立了电梯钢丝绳的纵向振动方程，通过数值计算推导出了钢丝绳的固有频率计算公式，并对电梯垂直振动的固有频率进行了分析，解释了电梯钢丝绳在提升过程中某行程阶段振动加剧的原因；Zhang等[4]以简化的轴向提升钢丝绳模型为基础，建立了集中参数的动力学运动方程，分析了提升钢丝绳做衰减振动、发散振动以及等幅横向振动的原因，并结合数值分析与试验对理论推导公式就行了验证；朱真才等[5-6]利用Hamilton原理建立了缠绕式提升机的运动微分方程，并提出该方法也适用于研究深井提升下矿车进罐时的振动特性；张鹏等[7-8]人以高速电梯提升钢丝绳为研究对象，运用Hamilton原理和Galerkin方法对进行动力学方程建模和求解，进一步对振型函数就行了修改，得到了更加精确的数值解；Kaczmarczyk等[9-10]利用Hamilton原理推导出了缠绕式提升机钢丝绳的纵向振动微分方程，并运用多尺度法分析了在周期的外部激励下提升系统的振幅和共振区域等；Kaczmarczyk等[11]研究了高速电梯提升系统的非线性和非稳态振动特性，并发现提升系统的参数变化会导致提升系统内部出现自参数共振现象。

单绳提升系统的振动特性研究比较多，但对于双绳以及多绳缠绕式提升的研究比较少，本文通过将容器看为平面运动的刚体，两钢丝绳通过容器连接进行耦合，建立了双绳多层缠绕提升模型，并分析两钢丝绳在圈间过渡不同步时，钢丝绳张力差及动张力的变化规律，为控制同一卷筒两缠绳区的两根钢丝绳缠绕不同步提供理论依据。

1 双绳提升系统动力学模型

1.1 无边界激励时提升系统的动力学方程

本文将双绳多层缠绕提升系统分为悬绳和垂绳部分，如图2所示。其中，将悬绳与卷筒的接触点作为坐标原点O1,O2，设两钢丝绳上任意一点p1,p2的长度为x1(t)，x2(t)天轮到原点的距离为Ls，两钢丝绳与提升容器的连结点到原点的距离分别为lv1(t),lv2(t)。对于悬绳段上的任意一点具有纵向、横向和侧向的位移，分别为uci(xi,t),wi(xi,t)和vi(xi,t)，其中i=1,2。对于垂绳段，由于天轮和罐道的限制作用，仅考虑其纵向位移ui(xi,t),其中i=1,2。

此外，对图2模型做出以下假设：①提升钢丝绳的材料均匀并假设为黏弹性体；②钢丝绳在卷筒和天轮上的缠绕没有相对滑动；③卷筒、天轮和提升容器均为刚体；④忽略钢丝绳的扭转特性和提升容器运行过程的空气阻尼；⑤忽略静平衡状态时，悬绳由于重力作用形成的垂度。

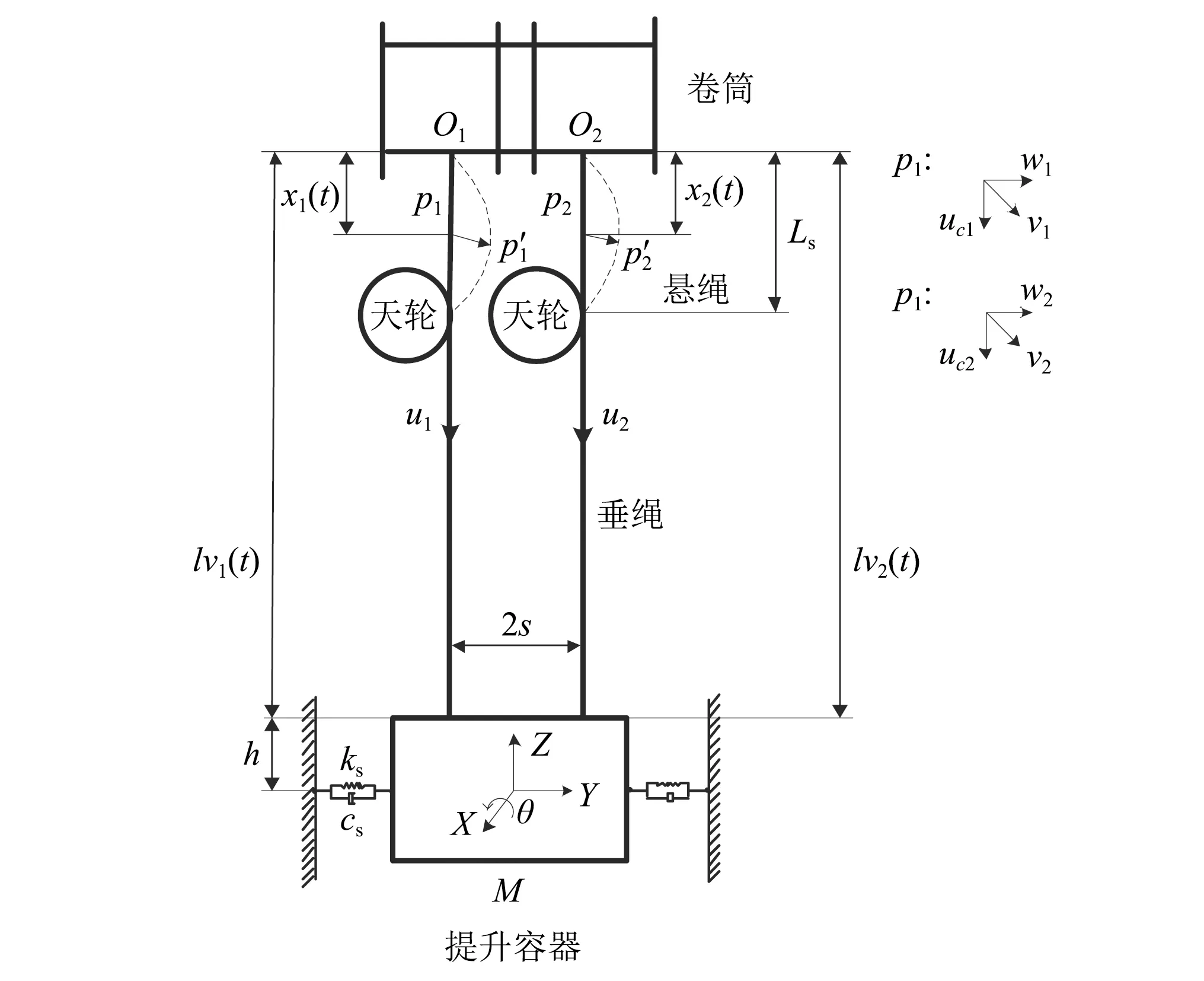
图2 双绳多层缠绕提升系统简化模型Fig.2 Model of the two cable mine hoisting system

此提升系统为非保守系统，可以采用分析力学中的变分方法，并结合广义的Hamilton原理对提升系统的动力学模型进行推导，即系统的动能和势能之差以及阻尼虚功在时间边界条件范围内的积分的变分为零。

(1)

式中：T为提升系统的动能；Ee为系统的弹性势能；Ep为系统的重力势能；W为系统阻尼所做的功。

假设两钢丝绳上任意一点p1,p2的位置矢量分别为

(2)

(3)

对位置矢量进行全微分可以得到相应的速度矢量

(4)

(5)

(6)

对于提升容器而言，假设其为平面运动的刚体，仅有绕X轴的旋转和沿Z轴的平移，则可以如图3所示，使用广义坐标(U,θ)来描述容器在提升过程中的运动规律，其中广义坐标可由如式(7)表示。

(7)

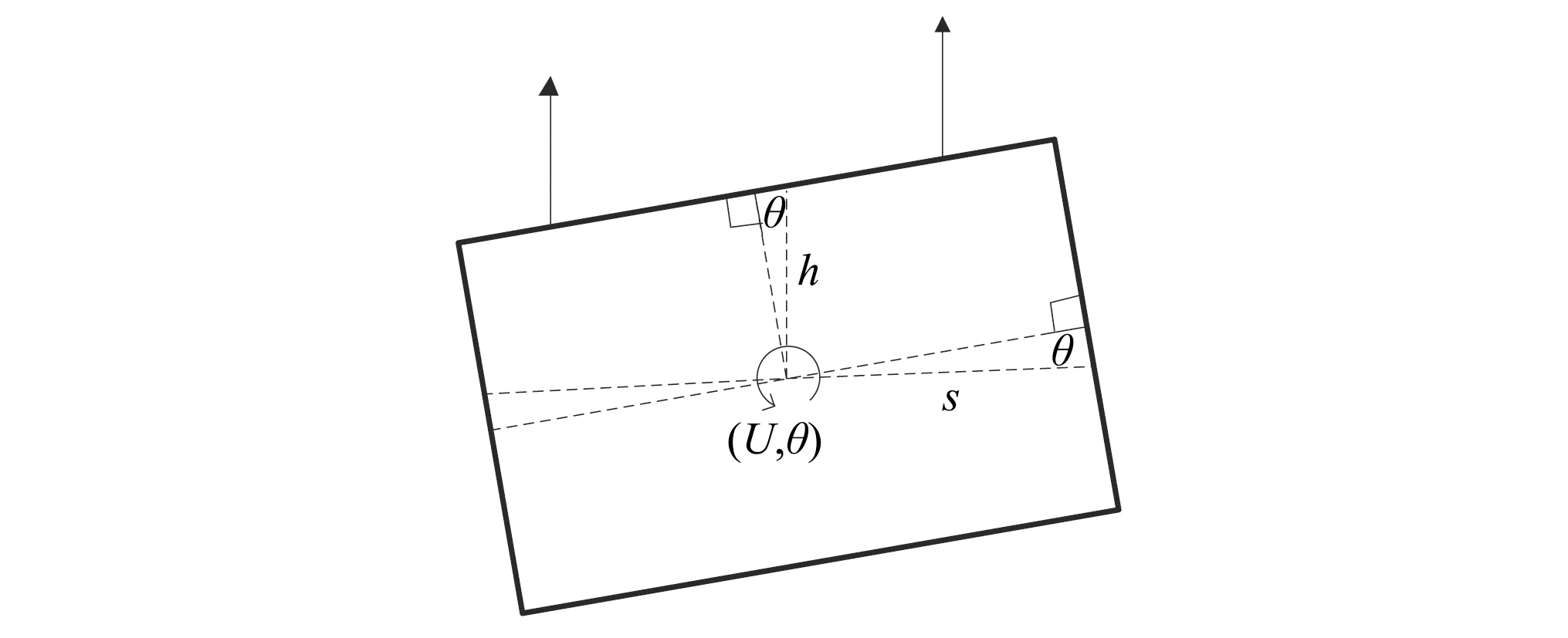
图3 提升容器旋转示意图Fig.3 Diagram of rotation of mine cage

容器在运动过程中由于两侧柔性罐道的限制作用，转动角度相对于容器尺寸而言较小，则cosθ≈1,sinθ≈θ，因此简化上式后可以推出U和θ的表达式为

(8)

提升系统的动能

(9)

提升系统的弹性势能

(10)

式中：E0为提升钢丝绳的初始弹性能；Tci,Tvi分别为悬绳和垂绳的准静态张力

(11)

εci,εvi分别为悬绳和垂绳段钢丝绳的正应变

(12)

提升系统的重力势能

(13)

式中：Ep0为提升系统的初始重力势能；第二项为两钢丝绳重力势能的改变量；第三项为容器重力势能的改变量。

钢丝绳在提升过程中的阻尼耗散能

(14)

式中:fcu,fcv,fcw为悬绳段钢丝绳沿钢丝绳轴向、沿卷筒径向和沿卷筒轴向的等效阻尼；fu为垂绳段钢丝绳的纵向等效阻尼。本文使用等效的黏性阻尼模型，其中各个阻尼的具体表达式为

(15)

将以上系统的动能、弹性势能、重力势能以及阻尼虚功代入式(1)，并利用以下时间和几何边界条件

(1)时间边界条件

(16)

(2)几何边界条件

(17)

利用变分原理，并结合以上时间和几何边界条件，根据独立变分不为零，同时运用变上限积分的莱布尼兹公式可以推出提升系统的动力学控制方程为

x2=lv2

(18)

其中，

(19)

1.2 边界激励下提升系统的动力学方程

由超深井提升的需要，卷筒必须满足多绳多层缠绕，其绳槽布置形式采用的是双折线平行绳槽，其简图如图4所示。其中绳槽间隙为ε，钢丝绳直径为d。此绳槽的特点是，钢丝绳在每经过一个过渡区时，沿卷筒轴向(d+ε)/2的排绳位移，且每次沿卷筒轴向移动(d+ε)/2的距离。对于第二层以及以上的钢丝绳在过渡区时与底层钢丝绳交叉相互作用，会造成沿卷筒径向的抬高位移。同时，在卷筒转过相同角度下，钢丝绳经过过渡区与经过平行区相比，会产生一定的弧长差，因此会对钢丝绳沿轴向，即沿卷筒切向会产生一个位移激励。

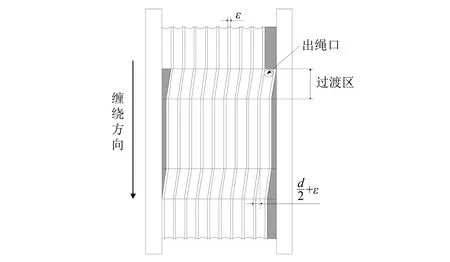
图4 双折线平行绳槽Fig.4 Groove of lebus

基于双折线平行绳槽的结构特点，在提升过程中沿卷筒三个方向的激励都是周期性的，因此可以建立周期性的边界激励函数来代替原有的边界条件。如图5所示，根据钢丝绳在经过过渡区时，沿卷筒轴向排绳的最大位移和径向抬高的最大位移，可以推导出沿钢丝绳的轴向的位移最大激励幅值。

因此沿卷筒径向、轴向和切向的最大位移激励幅值可以表达为

(20)

(21)

(22)

式中：Rd为卷筒的半径；ψ为过渡区对应的圆心角；n为钢丝绳缠绕层数；d为钢丝绳的直径。

以下使用三角函数来模拟沿钢丝绳轴向的周期边界激励函数，具体表达式为

(23)

式中：tψ为提升过程中经过过渡区的时间tψ=ψRd/V；V为提升速度；te为提升过程中连续经过一个直线区和一个过渡区的总时间；te=πRd/V，α=πV/ψRd。

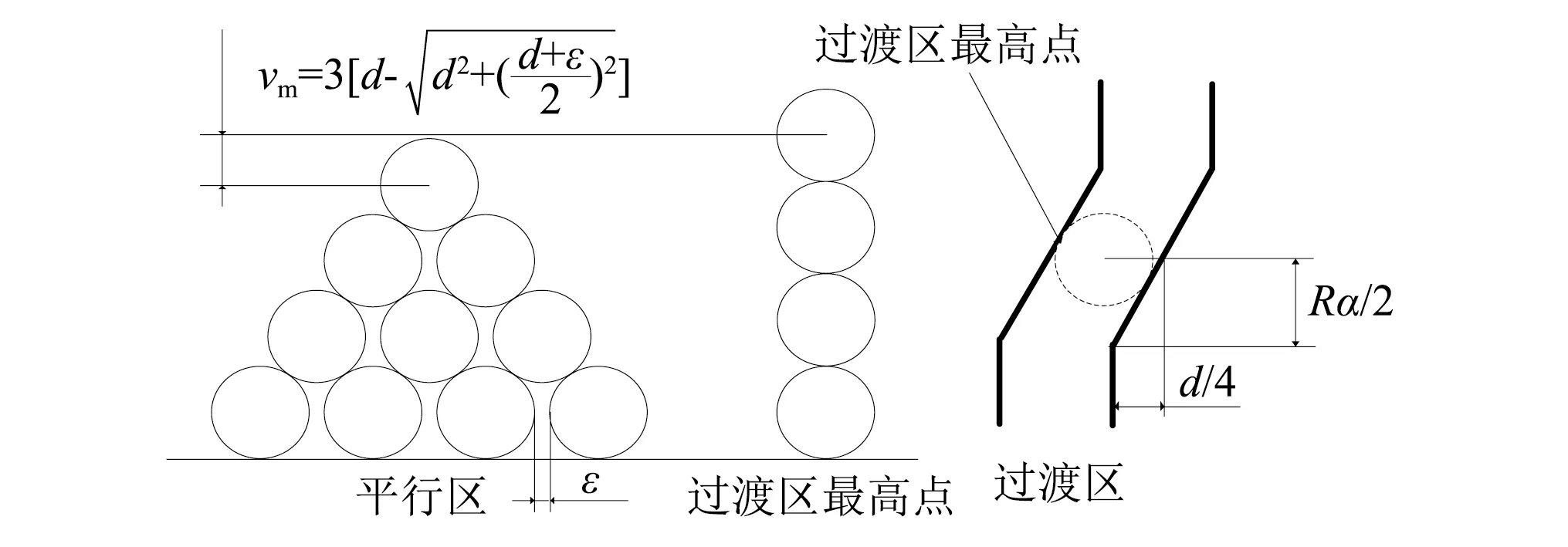
图5 平行区和过渡区钢丝绳堆叠简图Fig.5 Stacking of wire rope in parallel and crossover zone

对式(12)中悬绳的应变公式进行变换，并考虑钢丝绳天轮处的力边界条件EA[εci-ui,xi(Ls,t)]=0，可以推导出

(24)

式(24)为垂绳的力边界条件，其中K=EA/Ls，通过天轮与垂绳相互作用，可以推导出垂绳段在边界激励下的动力学方程为

(25)

式中：

(26)

ρr=ρ+Msδ(xi-Ls),i=1,2

(27)

2 方程离散化

本文钢丝绳的力学模型采用的是分布式参数连续体，其推导出的动力学方程组为无限自由度的偏微分方程组，且方程系数是时变的，因此难以求解出其精确解。以下使用Galerkin方法将其离散化为常微分方程组，并通过MATLAB编程进行数值近似求解。

2.1 形函数求解

对于垂绳段钢丝绳，其纵向振动可以参考杆的纵向振动[13]，因此钢丝绳的自由振动方程可以假设为

(28)

对于以上二阶偏微分方程具有以下形式的通解

ui(xi,t)=ψ(x)ejωt

(29)

且ψ(xi),ω满足如下特征方程

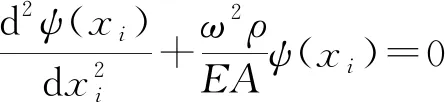
(30)

式中：E为钢丝绳的弹性模量；A为钢丝绳的有效截面积；ψ(xi)为振型函数；ω为振动频率；C1，C2为待定系数，且有β=ω2ρ/EA。

由钢丝绳在天轮处和容器处的力边界条件

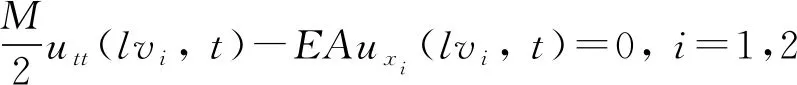
(31)

将其代入式(30)，可以推导出提升系统频率的超越方程为

(K-Msω2){Mω2sin(βlvi)-EAβcos(βlvi)+

EAβ[Mω2cos(βlvi)+EAβsin(βlvi)]}=0,i=1,2

(32)

和垂绳段振型函数为

(33)

2.2 离散偏微分方程组

将两钢丝绳的振动位移u1,u2改写为向量形式

(34)

式中：ψ=(ψ1,ψ2,…,ψn)T为振型函数组成的列向量;p=(p1,p2,…,pn)T,q=(q1,q2,…，qn)T为广义模态坐标组成的列向量，n为所取的振型阶数。

将式(34)代入有边界激励的钢丝绳动力学控制方程组式(25)，并同时在左边乘以一个列向量ψ，同时在(0,lvi)范围后对xi进行积分，既可以将原来无限自由度的偏微分方程组离散化成常微分方程组

(35)

式中：M1,M2为广义模态坐标所对应的时变质量矩阵;C1,C2为对应的时变阻尼矩阵;K1,K2为对应的时变刚度矩阵;F1,F2为对应的广义力矩阵；m3,m4,m5和m6为容器处广义模态坐标所对应的时变质量矩阵;c3,c4,c5和c6为对应的时变阻尼矩阵;k3,k4,k5和k6为对应的时变刚度矩阵。

3 数值计算及结果分析

本文以某大型超深矿井多层缠绕提升系统为例，分析了当两缠绳区由于圈间过渡激励不同步时，两缠绳区过渡不同步时形成的圆心角大小与两钢丝绳张力差值的大小关系，同时分析了在不同提升速度下，张力差的变化情况。提升系统的具体参数见表1。

表1 超深井提升系统参数Tab.1 Parameters of the deep mine hoisting system

在实际的矿井提升过程中，提升系统会经历慢加速、加速、匀速、慢减速、减速和停车等阶段，为了简化模拟运行曲线的函数，仅采用三阶段的运行曲线图，如图6所示。

超深井提升具有高速、重载、大惯量的特点，在提升过程中两钢丝绳在圈间过渡时经过折线区可能不同步而形成一定的圆心角差β，如图7所示。

图6 三阶段提升速度图Fig.6 Diagram of three-stage hoisting speed

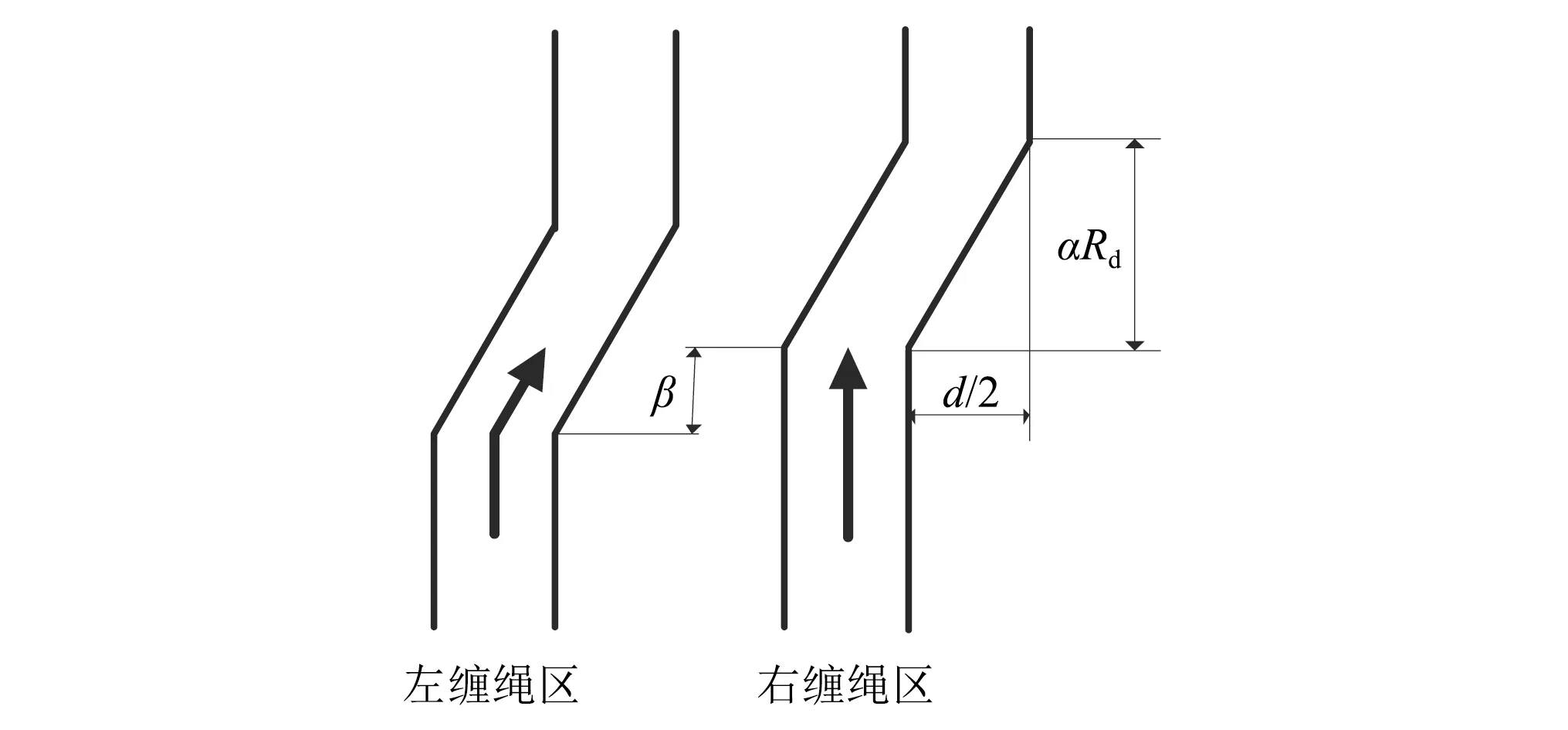
图7 左右缠绳区过渡不同步Fig.7 Non-synchronous transition between two crossover zones

过渡区圆心角大小一般取15d/Rd[15]，由表1参数计算可知，过渡区圆心角α可取为0.285 rad。以下分别以两绳区过渡圆心角差值β为0.01 rad,0.02 rad,0.025 rad,0.03 rad,0.035 rad,0.04 rad,0.045 rad时来分析提升系统的动张力差。

对式(35)进行数值求解，可得到在不同提升速度下随时间变化的广义模态坐标[16-17]，并根据式(34)可以得到相应的振动位移[18]。由于垂绳段靠近天轮处的点所受张力最大，以下取垂绳段上天轮处的点来进行动张力计算，根据黏弹性力学，其计算公式为

(36)

根据式(36)可以计算出两钢丝绳在提升过程中的动张力变化曲线[19]，进而可以得到提升过程中两绳张力差随时间变化的曲线。其中β=0.01 rad时钢丝绳张力、张力差及动张力见图8、图9，其余值详见表1。

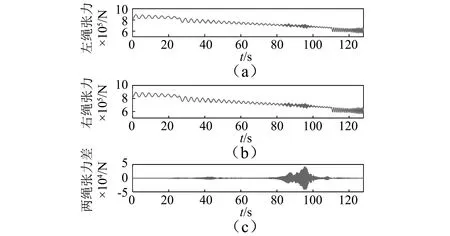
图8 β=0.01 rad,V=18 m/s时垂绳段两钢丝绳在天轮处的处张力及张力差Fig.8 Vertical cable tension and tension difference at the sheave,when β=0.01 rad,V=18 m/s

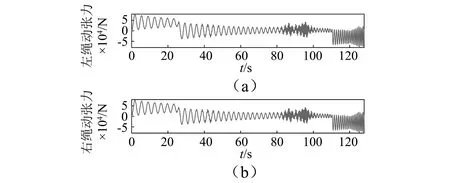
图9 β=0.01 rad,V=18 m/s时垂绳段两钢丝绳在天轮的动张力Fig.9 Vertical cable dynamic tension difference at the sheave,when β=0.01 rad,V=18 m/s

图10 不同速度激励频率及垂绳固有频率Fig.10 Different speed excitation frequency and vertical rope natural frequency

由图8可知，两钢丝绳的张力随着提升时间的增加，钢丝绳的张力是逐渐减小的[20-21]，原因是随着提升高度变化，垂绳段的钢丝绳质量不断减小；同时由于提升过程中由于纵向振动而产生的动张力，钢丝绳总张力曲线是一条沿右向下倾斜的振动曲线；其中两钢丝绳的最大张力差是出现在提升时间段为t=80～100 s。由图10可知，当提升速度为V=13～20 m/s时激励频率与垂绳二阶、三阶固有频率都存在交点，在此提升速度范围内都会有垂绳发生共振，由于钢丝绳内阻尼的作用，振幅快速衰减。由激励频率Ω=2V/Rd，当V=18 m/s时，圈间过渡的激励频率与垂绳固有频率存在一个交点，结合图9，图10可知，在此时刻附近由于圈间过渡激励频率与垂绳固有频率接近而产生了共振；同时本文中张力差主要是由于两钢丝绳振动相位不一致而产生的，振动相位不一致主要来自圈间过渡激励不同步而形成的，即与两绳在圈间过渡形成的圆心角差相关，如图7所示。在未发生共振时，圈间激励引起的垂绳振动较小，因而由于振动相位不一致形成的张力差较小，而共振阶段振幅较大，从而导致V=18 m/s时钢丝绳最大张力差出现在共振区域，对于其他提升速度也是仅有圈间过渡不同步而造成振动相位不一致而形成张力差。综上所述，由于振动造成两绳的张力差大小主要由两个因素共同决定：①两钢丝绳振动相位差是多少，即激励函数的相位差是多少；②两钢丝绳振动幅值的大小。