基于翼型凹变的叶片结构动力学性能优化方法研究

马剑龙，霍德豪，李学彬，段亚范，吴雨晴，汪建文

(1.内蒙古工业大学 能源与动力工程学院，呼和浩特 010051；2.风能太阳能利用技术教育部重点实验室，呼和浩特 010051)

随着风能多元化应用推广的深入，风力机翼型和叶片的成功开发是风力机设计中提升风能利用率、解决机组运行失稳和结构疲劳损伤的基础性问题。然而，风力机产业快速发展的30年中，诸多气动性能优异的分布式风电叶片在远短于设计寿命期内频发疲劳损伤事故而导致产品夭折的事件屡见不鲜。分析其原因：由于风力机叶片朝着大型化的方向发展并采用轻型材料，使得叶片柔性增大、结构刚度降低、固有频率下降。此外，在实际运行中叶片在吸力面处的气流交汇也会更加的复杂，使得叶片气动性能及运行稳定性上有大幅度的下降。进而导致叶片振动响应增强，疲劳损伤加剧。介于此，在分布式风力机现有翼型成果基础上提出一种即可保持叶片气动性能，亦可有效改进其结构动力学性能的结构改进方案不失为一种技术捷径。之前的研究中，研究人员对叶片的结构改形多着眼于翼型前、后缘点处结构形式的改进，本文拟另辟蹊径，以某分布式风力机叶片为研究对象，针对其吸力面翼型曲线进行结构凹变，探究结构变化对风轮整体气动性能和结构性能的影响特征，进而探索翼型凹变在叶片设计中应用的可行性。

近年来，翼型整体的优化设计方面的相关典型研究如：Grasso[1]开发了ECN-G1-21翼型，并利用缩比实验进行了不同雷诺数时翼型气动性能测试及失速分析；Mohamed[2]则针对达里厄风力机进行了新翼型设计；Wang[3]提出了一种考虑连续攻角变化的新的翼型设计方法，并提出了基于泰勒高阶多项式的风力机专用新翼型设计方法[4]；Liu等[5]则开发了一种新的翼型结构参数化设计方法，并将其应用于DU93-W-210翼型的优化，进而佐证了该方法的先进性；Mei等[6]建立了一种专门针对于H型垂直轴风力机翼型的设计方法；Bedon等[7]利用优化的遗传算法开发了一种翼型结构的改良方法；Tartuferi等[8]则开发了适用于Savonius风力机的专用新翼型；Birajdar等[9]开发了专门针对于小型风力机叶片设计的两种新翼型IND 15045和IND 09848。

翼型局部的优化设计方面的相关研究如下：Menon等[10]进行了尾缘开槽对叶片气动载荷的影响分析；Cai等[11]研究多种前缘突起对叶片气动性能的影响，发现流体经过凹凸前缘时具有周期性和对称性；Liu等[12]通过对叶尖结构进行凹槽设计，并利用PIV拍摄叶尖附近流场，发现叶尖开槽可以减弱叶尖涡的强度并加速耗散；Ahmed等[13]在不同雷诺数下在叶片前缘添加襟翼，发现前缘襟翼可以有效的增加小型风力机的气动性能；Wang等[14]通过风洞试验对DU40光滑翼型,DU40-llwavy和DU40-25wavy两种仿生凹凸前缘翼型，进行流场测试发现，凹凸前缘能够有效的延缓流动分离现象Hansen等[15]通过研究发现：凹凸前缘在叶片未失速时会提升翼型的升力系数，在失速状态下，可以减小升力系数的损失；Sun等[16]设计一种新的后缘襟翼，可以有效的降低叶片根部的弯矩以及疲劳损伤。

综合文献分析可知，所见研究对叶片翼型的改良往往着眼于翼厚、翼型前/后缘点处结构优化改进为设计理念，专门针对于翼型中部曲线的优化研究较少，而利用该理念在设计工况下以不降低叶片功率输出为前提的叶片结构动力学性能有效改进方法的相关研究则未见报道。

1 翼型结构凹变提出的理论依据

如图1所示，风力机叶片旋转过程中，因压力面气压值高于吸力面，故各翼型面前、后缘点处均存在由压力面流向吸力面的气体环流，两处环流最终于吸力面某处交汇，交汇的存在将导致叶面气流能量损失的增加，并影响叶片运行的稳定性。本文通过合理选择凹变位置、形式及几何尺度可实现对交汇流线的引导及其影响范围的限制，从而减小吸力面气流的脉动及能量损失。基于上述分析，翼型凹变有可能不降低或在一定程度上提升叶片的做功能力；同时，翼型凹变将改变叶片外形结构及质量分布，故可在一定程度上改变叶片的刚度、阻尼比及其他结构参数，由此可获得一种在不降低叶片气动性能前提下其结构动力学性能有效改进的实现方法。

图1 翼型吸力面流线的交汇Fig.1 Convergence of the flow line on the airfoil suction surface

2 翼型凹变的实现方法

以图2(a)所示某翼型结构为例，假设翼型吸力面的绕流交汇线往往出现在距离前缘M处，选取该处为翼型向内侧凹变的中心点。考虑到翼型弦长显著大于厚度的结构特征，凹变结构对应选择为椭圆面，令椭圆面中心点与凹变中心点重合，椭圆面长轴为A、短轴为B，并使椭圆面长轴与凹变中心点处翼型曲线相切，本例中椭圆面长轴与弦长的夹角α为2.25°，凹变翼面与非凹变翼面间采用B样条曲线光滑过渡搭接，具体实现过程如图2(b)所示。

(a)原翼型

(b)凹变翼型L-翼型弦长;M-翼型曲线上凹变中心点到翼型前缘的距离;A-椭圆面长轴长;B-椭圆面短轴长图2 翼型凹变原理Fig.2 Principle of airfoil concave

3 翼型凹变对风轮气动性能的影响

3.1 数值仿真模型的建立

3.1.1 凹变翼型叶片的生成原理

叶片为木质实心结构，长为0.7 m，叶片翼型部分设置有10特征翼型面，各翼型面之间的部分通过放样实现，1翼型面和2翼型面的间距为35 mm，其余相邻翼型面间距为70 mm。将原翼型中的10特征翼型面曲线进行相应的结构凹变并放样后即可获得凹变翼型叶片，如图3所示。

图3 凹变翼型叶片的生成Fig.3 Generation of concave blades

3.1.2 计算模型的建立

数学模型依据内蒙古自治区新能源试验示范基地所属B1/K2型低速风洞建立，如图4所示，目的是利用相应的试验佐证算法的可靠性。

图4 数学仿真模型Fig.4 Mathematical simulation model

计算域划分为旋转域和静止域两部分，旋转域包裹风力机叶片，通过域的旋转实现叶片的转动。旋转域采用六面体网格，静止域采用四面体网格，两域间采用滑移网格，数据传递采用INTERFACE技术。静止域采用网格膨胀技术，全域实现了网格的分层划分，多种网格划分技术的综合应用可实现计算资源的高效利用。

3.1.3 计算方法及结果分析

采用非稳态算法，考虑到叶片旋转过程中，伴随着较强的逆压梯度和流动分离，故所采用算法模型需考虑湍流剪切应力效应，并对涡流黏度不产生过度预测，SSTk-ω湍流模型在上述问题解决方面具备显著的优势。且壁面采用固体无滑移条件，入口条件采用速度入口，出口条件采用自由出口，网格间数据的传递采用二阶差分格式。

原翼型叶片额定风速为10 m/s，设计尖速比为5，针对此工况进行原翼型风轮气动性能的计算，如表1所示。

表1 原翼型风轮气动性能Tab.1 Aerodynamic performance of 3 types of wind wheels

3.2 叶片气动性能可靠性试验

3.2.1 测试对象

测试对象，如图5所示，为与模拟计算使用相同叶片的某木质叶片表面涂有玻璃钢材料，轮毂采用法兰连接。

图5 叶片实拍图Fig.5 Pictures of physical blades

3.2.2 测试方法

通过吹气式B1/K2低速风洞提供稳定来留风速，风轮电机输出端与负载系统和NORMA5000 型功率分析仪设备连接，以此获取风力机的功率参数如图6所示。

图6 功率监测方法Fig.6 Power monitoring method

3.2.3 测试结果

实验结果如表2所示，定义相对误差=(计算值-实验值)/实验值×100%。

表2 实验功率与模拟功率对比Tab.2 Comparison of experimental power and analog power

由表2可知，模拟计算功率与实验功率在风轮的设计工况下功率相对误差为4.7%，因此模拟计算具有较高的可信性。

3.3 翼型凹变几何参数的确定

一方面，经过模拟计算后发现，翼型凹变过浅，对叶片吸力面流线的控制不明显，而凹变过深，则会使叶片凹变处过薄，增加了断裂的风险。通过模拟计算后，测得当椭圆长轴A为弦长C的6.3%、短轴B为翼型弦长C的1.5%时，该凹变形状对于流线控制较强，而且不会使得凹变处过薄，则选取该形状参数为本文凹变形状。另一方面，在设计工况下,叶片吸力面流线交汇，一般出现在叶片吸力面0.7～0.9倍弦长处，因此，选取翼型0.7倍、0.8倍、0.9倍弦长处进行凹变。同时，为了使得，凹变叶片能够对其结构性能产生一定程度的影响，综合考虑之下选取凹变长度为350 mm和420 mm两个长度最为适宜。进而通过模拟计算后得出，原翼型风轮与不同凹变翼型风轮在设计工况下的气动性能，如表3所示。

表3 a～g风轮气动性能Tab.3 Aerodynamic performance of a～g wind turbine

由表3中数据可知，设计工况下，b类风轮转矩较原翼型风轮略有增大，分析其原因为：翼型向内侧凹变后，吸力面的交汇流线规则地沿凹槽发生流动，较好地限制了交汇流线随工况变化于叶片位置的迁移，如图7所示；同时，翼型向内侧凹变，一定程度上限制了流线交汇处湍流的扩散，减小了吸力面气体的流动能量损失。因此，也可认为b类风轮相较于其它凹变风轮，对于流线的控制更为优异，使得其功率较原风轮有1%的提高。较好地实现了翼型凹变对叶片气动性能微影响的设计初衷。

图7 凹变叶片对吸力面流线交汇的控制Fig.7 The control of the confluence of a concave blade on the streamline of the suction surface

同时，为了探究在翼型其它弦长处进行凹变，是否对叶片的气动性能的提高有更好的影响。进而尝试在叶片的0.2～0.6倍弦长处进行长度为350 mm的凹变，并进行模拟计算获得其转矩值如表4所示。

由表4可知在翼型0.2～0.6倍弦长处进行凹变后，1～6类风轮转矩有显著的降低。对风力机的气动性能降低影响较大。因此下文主要对a～f类凹变风轮进行结构动力学性能的模拟与实验。

表4 1～6类风轮气动性能对比Tab.4 Aerodynamic performance of wind wheels

4 翼型凹变对叶片结构动力学性能的影响

4.1 翼型凹变对叶片刚度的影响

4.1.1 测试对象及传感器布置

测试对象为课题组某木质原叶片与b类凹变叶片，如图8所示，其翼型与模拟计算相同，表面涂有玻璃钢材料，轮毂采用法兰连接。

图8 b类凹变叶片与传感器布置Fig.8 Pictures of physical blades and arrangement of sensors

4.1.2 测试系统、测试原理及方法

测试系统采用 B &K 公司最新研发的PULSE16.1结构振动分析系统。测试原理如图9所示。

图9 模态测试原理Fig.9 Principle of modal test

测试方法采用瞬态激振法，单点激励，多点响应。激励信号由力锤人工施加，力锤所产生的激励信号由其手柄处的数据线传输给数据采集卡;叶片产生振动后，由加速度传感器感知测点处的振动信息，并由数据线传输给数据采集卡;数据采集卡收集数据，并对数据进行相关处理后，通过网线传输给电脑中的 Pulse 系统控制程序;控制程序完成测试系统的整体设置、控制及测试数据的显示、保存等功能。

4.1.3 测试结果分析

将数据导出到Reflect中进行后处理分析得到g类叶片与b类凹变叶片在一阶、二阶的振动频率及对应的阻尼比，如表5所示。

表5 不同风轮振动频率及阻尼比Tab.5 Vibration frequency and damping ratio of different wind turbines

从表5中可以明显看出b类叶片相较于与g类叶片在，一阶、二阶固有频率有2%和1%的增加、阻尼比有9.22%和3.4%的增加。分析其原因：当叶片被力锤敲击时的振动形式，可以看做为一个单自由度有阻尼的振动形式。

则叶片静刚度

(1)

式中：f为固有频率；k,m为刚度与质量；ζ为阻尼比。

通过承重得到，b类叶片较与g类叶片质量减少为Δm=8 g(减少量为1%)，进而将其与阶频率及阻尼比代入公式，计算得到b类凹变叶片与原叶片的刚度差Δk的增量为32%，由此可得，b类凹变叶片能够有效的增加叶片的静刚度。

同时，由于风轮在实际工况运行下是动态的，所以计算叶片的动刚度，才能真实的反应出叶片在运行工况下的刚度变化。

其运动方程为

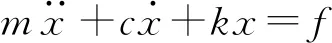
(2)

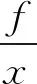
(3)

则动刚度

K=k-mω2+ciω

(4)

式中:k为静刚度；m为质量；ω为风轮旋转角速度；c为阻尼系数。

通过静载试验计算出物体静刚度增加量为32%，则在设计工况下，根据公式推导出凹变翼型叶片的动刚度也有很大程度的增加。

综合静刚度与动刚度的变化发现，凹变叶片一阶、二阶阻尼比的上升使得叶片振动消减速度变快，相同工况下对叶片的疲劳损失也会有很大程度的下降。同时，由于小型水平轴风力机的主要运行工况频率多发生在叶片一阶与二阶固有频率左右，凹变叶片在一阶、二阶振动频率上的提高，使得运行工况偏开叶片固有频率，减少断裂的风险。

4.2 翼型凹变对叶片最大位移及应变的影响

由于风轮叶片为实体木质，刚度较大，算法可以采用单向流固耦合计算。首先通过流场计算，得到风压载荷，进而将气动力、离心力、重力等加载到风力机，进行有预应力的结构场计算，最后得到叶尖位移与应变的大小。以a类风轮为例，通过模拟计算，求得叶片位移与应变振型，求得具体参数如表6所示。

表6 叶尖位移及应变量值Tab.6 Tip displacement of single leaf blade

由表6可知，b类凹变叶片，相较于其它叶片最大位移以及应变减少量最为显著，分别为28%和19%。分析原因：一方面，通过上文实验验证，翼型凹变后叶片刚度相较于原叶片很大程度的提高，同时，刚度提高使得叶片在外力作用下产生的弹性变形降低；另一方面，翼型凹变能在一定程度上限制了流线交汇处湍流的扩散，减小了吸力面气体的流动能量损失，使得吸力面湍流度降低，即对于叶片的扰动下降。综上两个因素，可以较好的解释叶片最大位移及应变有显著的下降的原因。

4.3 模拟计算结果的验证

由于实验条件所限，无法在实验中直接测得叶尖最大位移的具体数值。本文为验证上述模拟计算结果的可靠性，进而对b类叶片与g类叶片，进行叶片应变的动态风洞实验。以此从侧面验证模拟计算的可靠性。

4.3.1 测试设备原理及测点分布

应变值采集装置采用旋转机械应力应变遥测分析系统 TST5925测试原理，如图 10 所示，该系统为国内首台专门针对风力机叶片动态应力应变信号采集设计的装置。

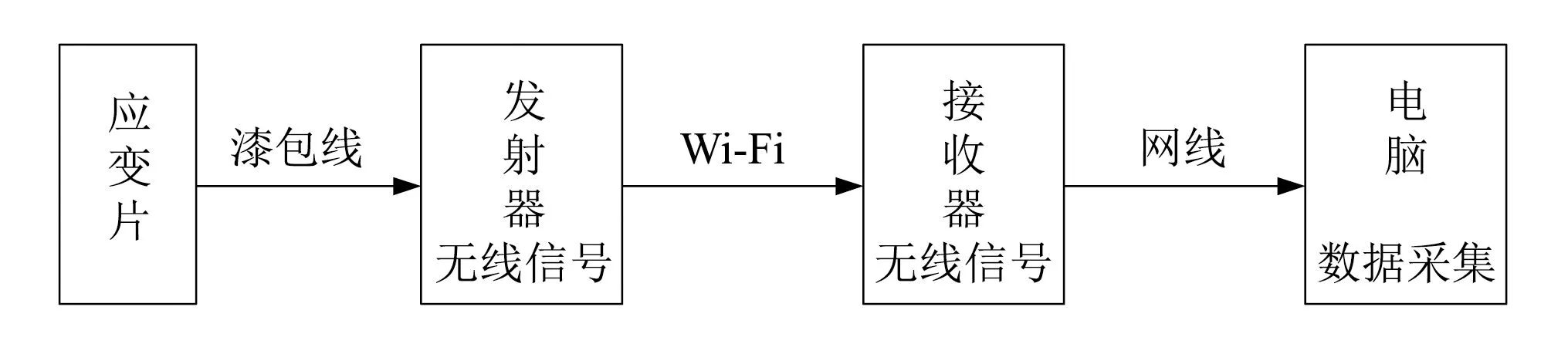
图10 应变值测试原理Fig.10 Principle of strain measurement

通过模拟计算观察发现叶片应变最大值，出现在叶跟0.17R处，即1号、8号、9号附近，并将其作为主要测试位置。叶片三阶以下振型的节点位于距风轮旋转中心处0.27R,0.51R,0.74R,0.85R，振幅较大，作为此次动态应变试验的辅助测试位置，如图11所示为应变片位于叶片迎风面与背风面的分布情况。

图11 应变测点分布Fig.11 Measuring-point distribution of strain

4.3.2 应变响应信号测试结果分析

通过试验测试得出，叶片最大应变值出现在叶跟处的1号测点，这与模拟计算结果的位置保持一致。则1号测点的实验结果如表7所示，定义相对误差=(计算值-实验值)/实验值×100%。

表7 1号测点实验与模拟应变对比Tab.7 Comparison of 1 point test and simulated strain

由表7知，设计工况下功率相对误差为3.7%与4.2%，较好的验证了上述模拟计算方法的可靠性。进而得出：翼型凹变叶片可以有效的减少叶片的最大位移及应变值，增加叶片的结构动力学性能。

5 结 论

针对某分布式水平轴风力机叶片开展翼型凹变的结构改进，本文首次提出于翼型吸力面上进行结构改形的探索，发现通过合理选择凹变位置、形式及几何尺度，可在一定程度提升叶片做功能力、提高风轮一阶、二阶固有频率及其阻尼比，并提升叶片静刚度与动刚度，进而减小叶片的应变值，使得叶片在外力作用下产生的弹性形变有显著的下降。翼型凹变的成功实现，不仅为风力机叶片翼型族的开发提供了新方法，同时可为诸多气动性能优异的风力机叶片在远短于设计寿命期内频发疲劳损伤事故而导致的产品夭折提供新的解决思路。

另一方面，本文所建立翼型凹变的方法，应可以成功地引用到大型风力机叶片设计，大型风力机叶片均采用中空的铺层结构，由理论分析可知，本文所提到的翼型凹变方式对大型风力机而言，均可一定程度上增强叶片的刚度，提高其固有振动频率，进而实现整机避振的结构改良。