浸液轴向变速运动黏弹性板的组合参数共振

张宇飞，刘金堂，闻邦椿

(1.东北大学 机械工程与自动化学院，沈阳 110819；2.沈阳航空航天大学 航空宇航学院，沈阳 110136)

在工程领域，轴向运动连续体具有非常广泛的应用。它存在于航天可伸缩结构、空中缆车索道、纸张生产、连续热镀锌生产线等工程应用中。因此，此类结构的动力学分析对于它们的安全运行具有重要的价值。

近些年来，轴向运动连续体的动力学引起了很多学者的研究兴趣。Pellicano等[1]分析了轴向运动梁的非线性振动与分岔现象。冯志华等[2]研究了轴向运动梁发生内共振时的稳定性。Wang等[3]基于经典板理论及非线性几何关系，建立了轴向运动功能梯度板的振动微分方程，并分析了系统的非线性动力学响应。Chen等[4]基于多尺度法，讨论了分析轴向运动系统的可解性条件。Zhang等[5-6]分析了具有轴向速度的黏弹性带的高维非线性动力学及混沌运动特性。张宇飞等[7]考虑具有轴向速度的复合材料薄壁圆柱壳，分析了系统的多模态耦合振动行为。Ding等[8]将Galerkin方法发展应用于轴向运动梁，并求解了系统在超临界运动中的自然频率。文献[9]针对移动载荷下的有限长Euler-Bernoulli梁，进一步探讨了Galerkin截断法在求解中的收敛性。Huang等[10]对横向载荷下轴向运动梁的1∶3内共振进行了研究。Yang等[11]采用有限差分法，分析了轴向运动板的非线性振动特性。Ghayesh等[12]考虑热载荷作用，讨论了轴向运动梁的非线性稳定性以及发生的混沌运动。张伟等[13]推导了轴向运动黏弹性带在平面运动下的非线性控制微分方程，然后采用多尺度法和离散法求解，分析了黏弹性传动带在内共振时的周期运动和混沌运动。Yang等[14]关注了横向振动与纵向振动相互耦合的轴向运动梁，并研究了在耦合运动下该陀螺系统的非线性动力学。

众所周知，轴向运动结构时常工作在液体环境中，这些情况多见于船舶工程、海洋工程、机械工程等。然而，对于轴向运动连续体与液体耦合振动的研究，现有文献还非常有限。对于轴向运动梁与液体的耦合振动，文献[15]关注该系统的固有频率并利用微分求积法进行了求解。Wang等[16-17]建立了浸没于液体中的轴向运动板的动力学模型，并对其线性和非线性自由振动特性进行了分析。张宇飞等[18]研究了轴向运动板与液体耦合的非线性自由振动及其发生的1∶1和1∶3内共振特性。

本文针对浸没于液体中的轴向运动黏弹性板，考虑其运动速度具有时变特性，并假定液体为无黏、无旋、不可压缩的理想流体，根据经典薄板理论及达朗贝尔原理，得到了该系统的横向振动控制微分方程。然后采用直接多尺度法对系统的偏微分方程及边界条件进行分析，利用可解性条件及Routh-Hurwitz判据确定了系统前四阶模态间的和式组合共振与差式组合共振的失稳区域。此外，研究了不同参数对上述两种组合共振失稳区间的作用。

1 基本方程

考虑浸入液体中的四边简支轴向运动黏弹性板，其力学模型和坐标系如图1所示。其中板密度为ρP，厚度为h；流体密度为ρf，板到左右刚性内壁的距离分别为h1和h2，水域宽度d=2.02 m。

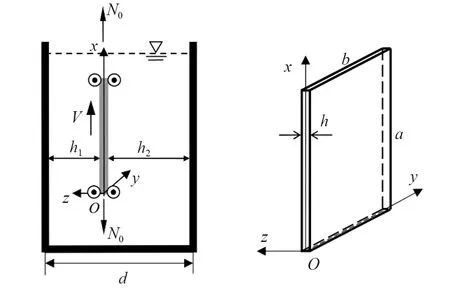
图1 浸液轴向运动黏弹性板Fig.1 Axially moving viscoelastic plate immersed in liquid

根据达朗贝尔原理，可推得浸液轴向运动黏弹性板的横向振动控制微分方程

(1)

式中：w为板横向位移；V为板的运动速度；Mx，Mxy，My，Nx，Ny，Nxy分别为板的三个内力矩和三个内力；Δp为流体动压力。

考虑几何关系、物理关系以及内力关系，可将式(1)用横向位移w表示

(2)

式中：D=Eh3/[12(1-μ2)]为板的弯曲刚度；μ为泊松比；η为黏弹性系数；N0为单位长度的面内张力；madd为附加质量面密度；表达式为

(3)

引入如下无量纲变量

(4)

将式(4)代入式(2)，得到系统的无量纲振动微分方程

(1-H)w,tt+(2-H)Vw,xt+(V2-1)w,xx+
(1-H)V,tw,x+ζ(w,xxxx+2ξ2w,xxyy+ξ4w,yyyy)=
-εη[(w,xxxxt+2ξ2w,xxyyt+ξ4w,yyyyt)+
V(w,xxxxx+2ξ2w,xxxyy+ξ4w,xyyyy)]

(5)

四边简支板的无量纲边界条件为

当x=0,1时

当y=0,1时

(6)

2 和式组合共振

设轴向速度具有如下扰动变化规律

V=V0+εV1sinΩt

(7)

式中：V0为平均速度；V1和Ω为速度脉动的幅值和频率。

将式(7)代入式(5)～式(6)，并应用直接多尺度方法，式(5)～式(6)的解可表示为

w(x,y,t;ε)=
w0(x,y,T0,T1)+εw1(x,y,T0,T1)+O(ε2)

(8)

且

(9)

将式(8)和式(9)代入式(5)～式(6)并分离ε0和ε1项，得

ε0：

(1-H)w0,T0T0+(V2-1)w0,xx+ζ(w0,xxxx+
2ξ2w0,xxyy+ξ4w0,yyyy)+(2-H)Vw0,xT0=0

(10)

(11)

ε1：

(12)

(13)

当发生和式组合共振时，系统固有频率满足如下关系

(14)

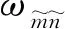
式(10)的解可写为

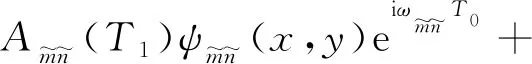
(15)

其中，

将式(14)～式(15)代入式(12)得

(16)

式中：NST为非久期项。

根据可解性条件，有

(17a)

(17b)

(17c)

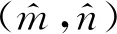
式(17)的解可写为极坐标式

(18)

将式(18)代入式(17a)和式(17b)得

(19a)

(19b)

式(19)的复数非零解可以表示为

(20)

式中：pi和qi(i=1,2)为T1的实函数。

将式(20)代入式(19)，并分离实部和虚部，得

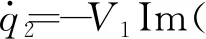
(21)

式(21)的特征方程可写为

λ4+β1λ3+β2λ2+β3λ+β4=0

(22)

式中：βi(i=1,2,3,4)由式(21)的系数确定。

式(22)的所有根均有负实部的充分必要条件为Routh-Hurwitz行列式均大于零，即

(23)

给定ξ=1,ζ=1,η=0.000 1,ρf=1 000 kg/m3，h=0.02 m,h1=1 m，图2给出了模态(1,1)与模态(2,1)，模态(1,2)与模态(2,2)间的和式组合共振在不同平均轴线速度下的不稳定区域，其中曲线上部表示不稳定区间。从图中可以看出，随着平均移动速度的增加，系统的不稳定区逐渐减小，组合共振的稳定区间增加。

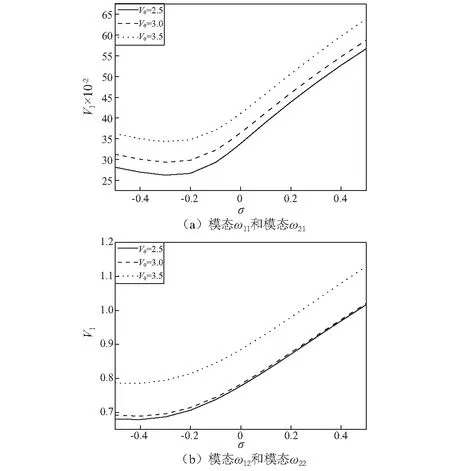
图2 不同平均速度下和式组合共振的失稳区域Fig.2 Unstable range for sum-type combination resonances with different axially mean velocities

给定ξ=1，ζ=1，η=0.000 1，V0=3和h1=1 m，图3给出了不同流体密度情况下模态(1,1)与模态(2,1)，模态(1,2)与模态(2,2)间的和式组合共振的不稳定区域。从图3可知，当流体密度逐渐增加时，轴向运动板和式组合共振的不稳定区域会随之增大。

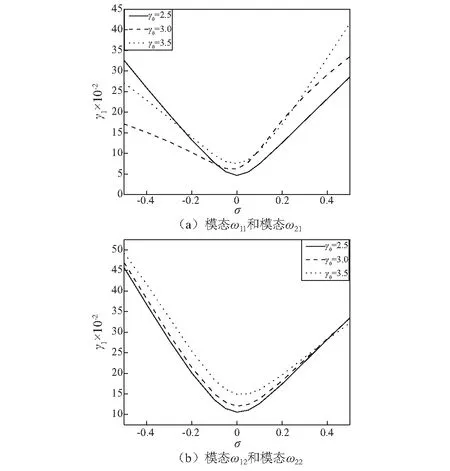
取ξ=1,ζ=1,η=0.000 1,ρf=1 000 kg/m3,V0=3，图4给出浸液板在不同位置时模态(1,1)与模态(2,1)，模态(1,2)与模态(2,2)间的和式组合共振的失稳区域。可以发现，当0.1 m

图3 不同液体密度时和式组合参数共振失稳区域Fig.3 Unstable range for sum-type combination resonances with different fluid densities

图4 板位置对和式组合参数共振失稳区域的影响Fig.4 Effect of plate location on the unstable range for sum-type combination resonances

3 差式组合共振

当速度脉动频率接近任意两阶固有频率之差时，系统将发生差式组合共振。考虑如下关系

(24)

式(10)的解表示为

(25)

将式(24)～式(25)代入式(12)，由可解性条件，得

(26a)

(26b)

(26c)

将式(26a)和式(26b)的解写为极坐标式

(27)

将式(27)代入式(26a)和式(26b)得到如下自治方程

(28a)

(28b)

式(28)的非零复数解为

(29)

式中：pi和qi(i=1,2)为T1的实函数。

将式(29)代入式(28)，分离实部和虚部，得

(30)

式(30)的特征方程可写为

λ4+β1λ3+β2λ2+β3λ+β4=0

(31)

式中：βi(i=1,2,3,4)由式(30)的系数确定。

所有根均有负实部的充分必要条件为Routh-Hurwitz行列式满足

(32)

令ξ=1，ζ=1，η=0.000 1，ρf=1 000 kg/m3和h1=1 m,图5给出了不同平均移动速度下模态(1,1)与模态(2,1)，模态(1,2)与模态(2,2)间的差式组合共振的失稳区域。从图中可以看出，模态(1,1)与模态(2,1)之间差式组合共振的失稳曲线出现偏转，但失稳区域的范围变化不大。对于模态(1,2)与模态(2,2)间的差式组合共振，随着平均速度的增加，失稳区间则逐渐减小。

图5 不同平均速度下差式组合共振的失稳区域Fig.5 Unstable range for difference-type combination resonances with different axially mean velocities

选取ξ=1，ζ=1，V0=3，η=0.000 1和h1=1 m，图6给出了不同液体密度下模态(1,1)与模态(2,1)，模态(1,2)与模态(2,2)间的差式组合共振的失稳区域。图6表明，流体密度的增加导致模态(1,1)与模态(2,1)间差式组合共振的失稳区域增加。对于模态(1,2)与模态(2,2)间的差式组合共振，失稳曲线则出现偏转，失稳区域也有增加的趋势。

图6 不同液体密度下差式组合共振失稳区域Fig.6 Unstable range for difference-type combination resonances with different fluid densities

图7给出了板在液体域中不同位置时，模态(1,1)与模态(2,1)，模态(1,2)与模态(2,2)间的差式组合共振的失稳区域的变化情况。其中各参数为ξ=1，ζ=1，V0=3，η=0.000 1和ρf=1 000 kg/m3。图7中表明，随着板与刚性内壁距离的增加，模态(1,1)与模态(2,1)间差式组合共振的不稳定区域减小。模态(1,2)与模态(2,2)间的差式组合共振的失稳边界线发生偏转，失稳区域也有减小的趋势。但是没有出现和式组合共振失稳区域先增加再减小的特征。

图7 板在不同位置时差式组合共振的失稳区域Fig.7 Unstable range for difference-type combination resonances with different plate locations

4 结 论

本文针对浸没于液体中的轴向变速运动黏弹性板，根据经典薄板理论及达朗贝尔原理，得到了系统的横向振动控制微分方程，根据多尺度法及Routh-Hurwitz判据，分析了系统前四阶模态间的和式与差式组合共振的失稳区域。结果表明：

(1)随着板平均移动速度的增加，和式组合共振的不稳定区域减小，模态(1,1)与模态(2,1)之间差式组合共振的失稳曲线出现偏转，而模态(1,2)与模态(2,2)间的差式组合共振不稳定区减小。

(2)和式组合共振与差式组合共振的不稳定区域均随着流体密度的增加而增加。对于模态(1,2)与模态(2,2)间的差式组合共振，失稳曲线出现偏转，失稳区域也有增加的趋势。

(3)组合共振的失稳区间与板在液体中的位置有关。当板距离刚性壁较近时，和式组合共振失稳更容易发生。随着板与刚性内壁距离的增加，模态(1,1)与模态(2,1)间差式组合共振的不稳定区域减小。模态(1,2)与模态(2,2)间的差式组合共振的失稳边界线发生偏转，失稳区域也减小。