两类阿贝尔Cayley图上的完全状态转移
2019-05-27张爱仙
张爱仙,吉 喆
(西安理工大学理学院,陕西西安710054)
完全状态转移(以下简称PST)对连续时间的量子步有重要影响,从而它在量子信息传输中有重要的应用。Bose在[1]中引入了量子网络中PST的概念,它是有限群的模拟。在2004-2005年,Christandel等[2]研究发现有两个顶点以及三个顶点的路,以及它们的笛卡尔幂在任意两个顶点之间有PST。Bernasconi等[3]得到有限个循环群Z2的直积上的gcd-图存在PST。Godsil在[4-6]中回顾总结了直到2011年PST以及几类图上周期的研究进展及结果,并分析了PST与代数组合,结合方案[7]等数学分支之间密切的关系。
此外,对距离正则图[7],完全二分图[7],Hadamard可对角化图[8]等图上的PST和周期的研究取得了大量的研究成果。Basic[9]和Cheung-Godsil在[10]中给出了循环图上(群G是循环群)存在PST的刻画方式。谭莹莹,冯克勤[11]给出了任意有限阿贝尔群上连通简单Cayley图(简称为阿贝尔Cayley图)上存在PST的刻画方式。本文中的计算方法和计算技巧受到了文献[12]中有限域上特征和理论的启发。
令Γ=(V,E)是连通简单图,其中V,E分别是Γ的顶点和边的集合,n=|V|≥2。A=A(Γ)=(αu,v)u,v∈V是Γ的邻接矩阵,定义如下:
(1)
由线性代数可知,A是n×n对称矩阵,且A的特征值均为实数,Γ的转移矩阵是以下方式定义的n×n的酉阵:
(2)
式中:u,v∈V,t∈R。
当u,v∈V,|Hu,v(t)|=1,则称Γ有在时刻t>0从u到v的完全状态转移(Perfect State Tranfer),以下简称PST。此时也称Γ在顶点u是周期的,周期为t。
1 预备知识
令G是有限阿贝尔群,|G|=n≥2,S是G的子集,|S|=d≥1。Cayley图Γ=Cay(G,S)定义如下:
V=G(顶点的集合)
(3)
E={(u,v):u,v∈G,u-v∈S}(边的集合)
(4)
假设0∉S,-S=S(即Γ是简单图),G=〈S〉(Γ是连通图)。Γ的邻接矩阵A=A(Γ)=(αg,h)g,h∈G,其中:
(5)
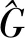
(6)
是A的特征值,且αχ为实数。
由有限阿贝尔群的结构定理可知,任意有限阶阿贝尔群G都可以分解为有限个循环群的直和,设:
G≅Zn1⊕Zn2⊕…⊕Znr(ni≥2)
(7)
其中Zni=(Z/niZ,+)。对每个x=(x1,x2,…,xr)∈G,其中xi∈Zni,有:
χx:G→〈ωe〉
(8)
(9)
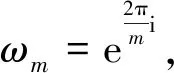
引理1[11]令Γ=Cay(G,S)是阿贝尔简单Cayley图,n=|G|≥3。设Γ在顶点(g,h)之间有PST,则:
1)Γ是整图,即对任意x∈G,αχx∈Z。
2) 如果α=g-h≠0,则α的阶是2。
现在假设g,h∈G,α=g-h≠0。由引理1可知,如果Γ在g,h之间有PST,则对任意

下面介绍2-adic指数赋值v2的概念,v2是如下映射:
v2:Q→Z∪{}
(10)
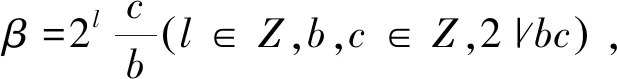
1)v2(ββ′)=v2(β)+v2(β′),
2)v2(β+β′)≥min(v2(β),v2(β′)),并且当v2(β)≠v2(β′)时,等号成立。
定理1[11]令Γ=Cay(G,S)是连通简单阿贝尔Cayley图,n=|G|≥3 ,d=|S|,则对g,h∈G,α=g-h≠0 ,Γ在g,h之间有PST当且仅当下列三个条件成立:
1)Γ是整图;
2)α的阶是2;
3) 对∀x∈G0,v2(d-αχx)≥m+1;
对∀x∈G1,v2(d-αχx)=m(m≥1)。
2 两类有限阿贝尔Cayley图上的PST

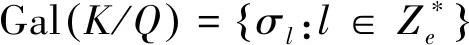
(11)
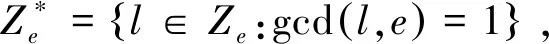
又有:
(12)



2.1 G=Z4⊕Z8上Cayley图存在PST
设S是G的子集合,计算这些等价类上的特征,计算结果见表1.
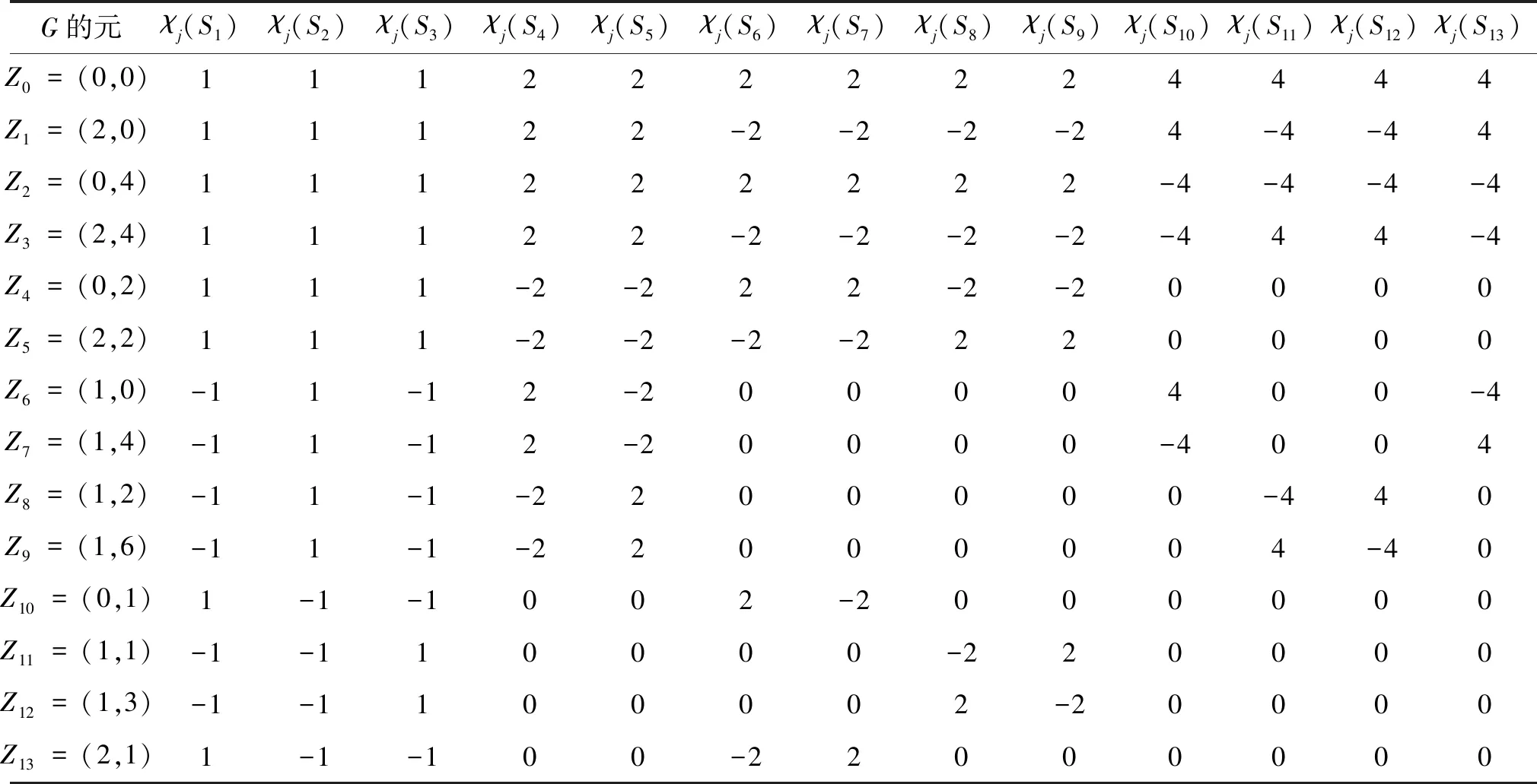
表1 G=Z4⊕Z8等价类上的特征

取α=(0,4)是G中的二阶元,很容易验证:
(13)
(14)

((d-χ0(S)),(d-χ1(S)),…,(d-χ9(S)))=(0,8,16,8,8,8,4,12,12,4)
(15)
((d-χ10(S)),(d-χ11(S)),(d-χ12(S)),(d-χ13(S)))=(10,10,10,10)
(16)
从而有:
v2(d-χj(S))=1,(10≤j≤13)
(17)
v2(d-χj(S))≥2,(0≤j≤9)
(18)
满足定理的条件,即Γ=Cay(G,S)中当g-h=α时,顶点g与h之间有PST。
2.2 G=Z8⊕Z8上Cayley图存在PST
S0={(0,0)},S1={(0,4)},S2={(4,0)},S3={(4,4)},S4={(2,0),(6,0)},S5={(0,2),(0,6)},S6={(2,4),(6,4)},S7={(4,2),(4,6)},S8={(2,6),(6,2)},S9={(2,2),(6,6)},S10={(1,1),(3,3),(5,5),(7,7)},S11={(1,3),(3,1),(5,7),(7,5)},S12={(1,5),(3,7),(5,1),(7,3)},S13={(1,7),(3,5),(5,3),(7,1)},S14={(1,0),(3,0),(5,0),(7,0)},S15={(1,2),(3,6),(5,2),(7,6)},S16={(1,4),(3,4),(5,4),(7,4)},S17={(1,6),(3,2),(5,6),(7,2)},S18={(2,1),(6,3),(2,5),(6,7)},S19={(2,3),(6,1),(2,7),(6,5)},S20={(0,1),(0,3),(0,5),(0,7)},S21={(4,1),(4,3),(4,5),(4,7)}。
取α=(4,4)是G中的二阶元,则:
(19)
(20)
取S=S8∪S16∪S18,|S|=10,容易验证〈S〉=G。由表2可知:
v2(d-χy(S))=1,y∈G1
(21)
v2(d-χx(S))≥2,x∈G0
(22)
从而满足定理的条件, 即Γ=Cay(G,S)中当g-h=α时, 顶点g与h之间有PST。
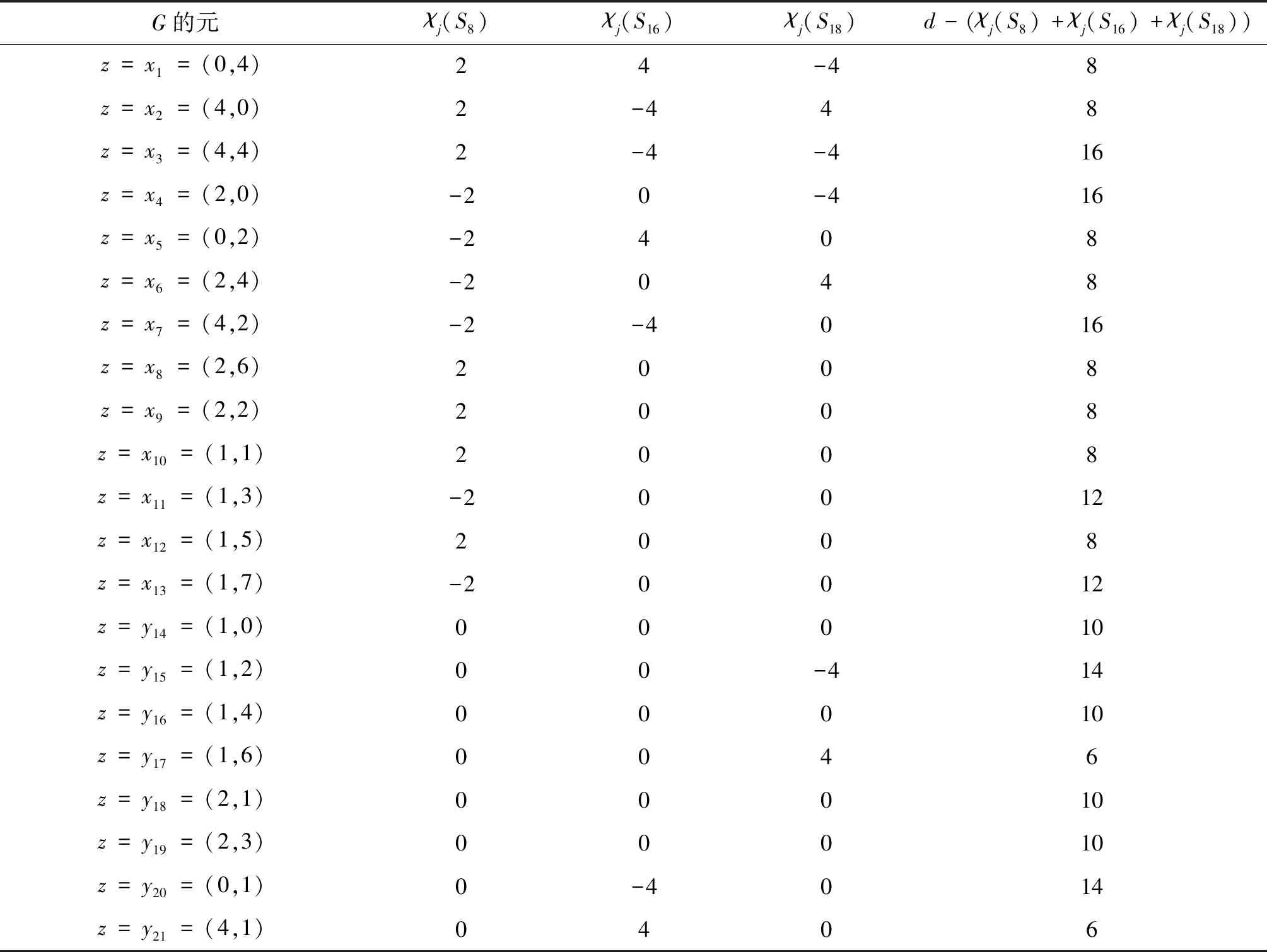
表2 G=Z8⊕Z8等价类上的特征(只列出部分)
3 结 论
本文利用有限阿贝尔群的结构定理,群上的特征,p-adic指数赋值以及群上的等价类等抽象代数和代数数论的知识,综合定理1给出的结果,通过计算得出了Z4⊕Z8,Z8⊕Z8上存在PST。
