泄水工程反弧半径的研究

2019-05-27宁利中徐泊冰宁碧波田伟利

西安理工大学学报 2019年1期

宁利中，徐泊冰，宁碧波，田伟利

(1.西安理工大学省部共建西北旱区生态水利国家重点实验室，陕西西安710048； 2.嘉兴学院建筑工程学院, 浙江嘉兴 314001；3.上海大学美术学院,上海200444)

泄水建筑物反弧段体型是泄水工程设计中的重要问题之一。许多科学工作者都在研究探索泄水建筑物反弧段的合理体型。在设计方面，国内外已建的水利工程中，其泄水建筑物末端挑坎绝大多数采用反弧曲线[1-3]，目前我国有关规范[4-6]中也规定反弧段采用圆弧曲线。前人在挑流鼻坎反弧半径选择方面做了大量的工作[1-3,7-15]。对泄水建筑物的水力特性也进行了研究[16-19]。本文根据收集的大量实际工程资料，在分析前人研究成果的基础上，经过量纲分析，给出了泄水建筑物反弧半径的一般表达式。进一步提出了挑流、面流、戽流的挑坎反弧半径选择方法，并对有关问题进行了初步讨论。

1 前人研究成果的分析讨论

从前人研究的目的、途径及特点来看，泄水建筑物反弧半径的研究可以分为两类，即应用工程资料反算的经验公式和通过系统试验或分析由某一极限条件得到的临界公式。现仅就前人建议的挑流鼻坎的经验公式作一简单的讨论。一般来讲，经验公式可分为以下几个方面。

1.1 “规范”中规定的方法

在我国现行的设计规范[4,6]中都规定泄水建筑物反弧半径的选择公式为：

R=(4～10)h

(1)

式中：R为反弧半径,单位为m；h为反弧水深，单位为m。

文献[5]则规定：

R=(6～12)h

(2)

类似式(1)的表达式还有R>ch、R=ch等[11],其中c为常数。

1.2 无因次表达式

1) Rao的公式[1]：

(3)

2) 文献[12]公式

通过考虑离心力对坎顶流速及挑距的影响，并加修正后，得：

(4)

式中：k为修正系数，面流时k=1,挑流时k=1.5；Z为挑坎顶以上坝高，单位为m；H为堰顶水头，单位为m。

3) 文献[13]的优化公式：

R/h=0.656Fr13/2

(5)

4) 文献[14]公式：

(6)

属于此类的还有印度波那中富水电研究所及标准协会[1]的公式等。

1.3 因次不和谐的经验公式

1) Chow的经验公式[2]:

(7)

式中：V为挑坎末端的平均流速，单位为m·s-1；H为堰上水头，单位为m。

2) 文献[14]提出的两个经验公式:

R=0.607E0.835q0.033

(8)

R=0.63E0.87

(9)

式中：q为单宽流量，单位为m3·(s·m)-1；E为鼻坎以上水头，单位为m。

此类公式国内外(1)还有许多，不一一赘述。

上述这些公式，均除式(4)以外仅适应于挑流鼻坎，其中式(7)～(9)量纲不和谐，式(7)、式(3)～(4)形式复杂，且已有研究表明,式(3)、式(7)的表达式也不尽合理[13]。“规范”规定的方法由于4.0R/h10的变化范围较大，设计也不易确定，因而有必要探讨既适合各种流态又形式简单、方便，合理的选择方法。

2 选择反弧半径的新公式

前人的研究成果表明,反弧半径的选择直接影响水舌挑距[7-8,15]、流速系数[9-10]、反弧段压力分布[11]等许多方面，虽然前人从上述不同方面出发做了大量工作，但是许多问题还未完全解决，同时很少见到考虑各个方面影响的系统研究，就前述各经验公式来说，也存在一定的差别。而目前实际工程中采用的设计指标是经过反复试验而定的，具有一定的根据(当然不一定是最优值)。因而本文在收集这些原型观测及模型试验资料的基础上，对各种流态的反弧半径取值问题提出了新的建议。

众所周知，在明流反弧段上，水流除受重力作用外，惯性力也起着重要的作用。根据反弧段的流动情况，反弧半径可以表示成g，h，V的函数，即R=f(g,h,V)。

由量纲分析，可以得到相对反弧半径为来流Froude数的函数：

R/h=f(Fr1)

(10)

式中水流Froude数正是惯性力与重力两种作用的综合反映[20]。

2.1 挑流鼻坎的反弧半径

前面已指出，关于挑流鼻坎的反弧半径研究资料比较多[1-6,8-15]，本文将收集到的滑雪道或长泄槽溢洪道、泄洪洞末端的挑流鼻坎情况的国内外36个工程的设计资料，根据式(10)的基本函数关系式，绘在R/h-Fr1坐标系中，见图1。可以看出，在坐标系中，两者随一定的规律变化，呈明显的条带形。若不考虑个别零散的点据，经分析其上包线的关系式为：

(11)

下包线的关系式为：

(12)

图1 挑流时时R/h随着Fr1的变化Fig.1 Variation of R/hwithFr1 in jet flow

为了设计方便，可取其点据的平均值作为设计指南，即：

(13)

式中3.0≤Fr1≤10.0 ，式(13)为挑流鼻坎的反弧半径计算公式。

将式(11)～(13)稍加变形，得：

(14)

(15)

(16)

由式(14)～(16)可以看出，反弧半径也可以表示成反弧段流速水头的函数，或者说反弧半径与流速水头之比在0.28～0.70之间变化。一般在初步设计时，可取其点据的平均值0.45作为设计的依据。

0.2≤R/E≤0.55

(17)

图2 挑流时 R/E和 K关系Fig.2 Relationship between R/Eand Kin jet flow

若再将文献[9]建议的临界关系式R/E=3.77K绘入图2，可以看出其大部分点据在曲线的上方，这说明实际工程中的反弧半径大部分大于临界半径，不会影响流速系数，依据上述资料给出的经验公式是偏于安全的。

2.2 面流挑坎的反弧半径

目前，关于面流挑坎反弧半径的原型及模型试验资料已积累了许多[2,11]，但很少见到面流挑流坎反弧半径的选择方法(12)。若仍采用式(10)的基本函数的关系式，以下游自由出流的相应的反弧挑坎的Froude数作为设计变量，则图3中45组资料的关系可以由下式表达，即：

(18)

式中：Fr1=2.1～6.0。

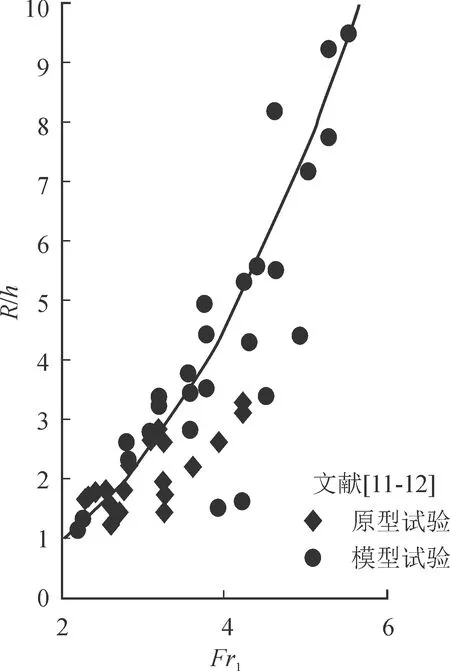
图3 面流时R/h随着Fr1的变化Fig.3 Variation of R/hwithFr1 in surface flow pattern

2.3 戽流挑坎的反弧半径

关于戽流挑坎反弧半径的选择问题，文献[9]对国内几个经验公式进行了介绍，但这几个公式不是直接研究反弧半径而获得。国外也有这方面的成果[1]。这里仍参照前面的处理方法，也以自由出流时相应的反弧挑坎Froude数作为设计变量，将收集到的28组原型及模型试验资料绘在图4的R/h-Fr1坐标系中，经分析得：

(19)

式中：Fr1=3.5～11.5。

图4 戽流时时R/h随着Fr1的变化Fig.4 Variation of R/hwithFr1 in bucket flow

另外，根据收集到E/R和K资料[21]，见图5所示。经过分析可得E/R和K的关系曲线为：

E/R=506.63K2-106.34K+8.1564

(20)

式中：0.01≤K≤0.155。式(20)也可以供设计时参考。

图5 戽流时时E/R随着K的变化Fig.5 Variation ofE/R with Kin bucket flow

3 讨论

1) 由图1、图3和图4可以看出，图3规律性最好，图1和图4规律性相当。然图1实验点据稍散，这主要是由于资料来自许多工程，而各工程的体形参数变化范围较大，加之测试方法，模型试验材料等也因人因地而异，另外设计指标也不一定是最优值等原因所致，这种现象从另一个角度也说明了上述各公式具有广泛的代表性。

3) 当挑流鼻坎反弧半径小于临界值时，流速系数和挑距突然减小，反弧段压力突然增大，水舌在反弧段形成旋滚不能起挑的问题，文献[8]已经进行了分析。而面流、戽流与挑流的临界条件不同，对于面流，在θ一定时，随着R的减小，坎长l=Rsinθ亦减小，这时对面流稳定则不利；而对单圆弧实体戽流，当R减小时，坎高a=R(1-cosθ)+C亦减小，下限水深亦减小。由此可见，对面流及戽流的临界条件需分别进行研究。