基于ELECTRE的犹豫二元语义多属性群决策方法

2019-05-27王秋萍肖燕婷闫海霞

西安理工大学学报 2019年1期

刘蕊，王秋萍，肖燕婷，闫海霞

(1.西安理工大学理学院，陕西西安710054；2. 西安理工大学高科学院，陕西西安710109)

在现实决策过程中，由于客观事物的复杂性，决策信息有时以“好”、“坏”、“一般”这样的语言术语来表达，但在以往处理语言评价信息的过程中，往往存在着信息损失和集结结果不精确的问题。为此，Herrera和Martínez[1]于2000年提出用由一个语言术语和[-0.5, 0.5)中的一个数值组成的2元组，即二元语义模型来处理语言信息，避免了语言评价信息集成和运算过程中出现的信息损失和扭曲的问题[2]。2016年，Beg和Rashid[3]进一步提出了犹豫二元语义信息模型的概念。该模型考虑到了决策者在[-0.5, 0.5)中的多个数值之间犹豫的情况，因此比二元语义模型更适合处理模糊性和不确定性。本文将研究属性值为犹豫二元语义信息的多属性群决策问题。

已有的大多数决策方法都是建立在承认属性间的完全可补偿性的假设之上的。也就是说，方案Ai在某个属性j1上比Ak差，而且无论差多少，都可以通过其他属性j(j≠j1)上的Ai≻jAk进行补偿，使方案对的总体比较结果为Ai≻Ak[4]。在实际决策过程中，这种处理方法有时是不合理的。比如，过期的食品即使很便宜人们也不会购买，即食品的价格属性不能完全补偿质量属性。因此，在决策过程中考虑属性间的部分可补偿性是非常有必要的。ELECTRE(法文Elimination et Choice Translating Reality的缩写)方法是一种基于级别高于关系[5-6]的多属性决策方法，它通过不和谐性检验反映决策人关于属性间的部分可补偿性。此外，该方法具有算理简明、过程清晰、对决策矩阵信息利用相对充分等特点[7]，众多学者对它进行了改进与应用[8-12]。文献[8]提出了犹豫模糊和谐集与不和谐集的概念，构造了强、弱级别高于关系，从而确定了方案间的排序。文献[9]提出了在区间二元语义环境下的ELECTRE和ANP的混合方法，其中，利用基于似然的偏好度定义和谐集、不和谐集和无差异集。文献[10]采用一种改进的ELECTRE方法[11]确定方案排序，以帮助消费者决定购买哪种农产品。针对决策信息为区间犹豫模糊集的决策问题，文献[12]提出了一种基于级别高于关系的决策新方法。

文献[12]将ELECTRE方法拓展到区间犹豫模糊决策环境中，受此启发，本文将ELECTRE方法拓展到犹豫二元语义决策环境中，提出了一种基于ELECTRE方法的犹豫二元语义多属性群决策方法。该方法基于犹豫二元语义可能度比较公式定义了犹豫二元语义和谐指数，结合文献[10-12]中的ELECTRE方法改进思想确定综合优势矩阵，并凭借净优势值对方案进行排序。最后，通过实例分析及与已有文献方法的比较分析说明所提方法的可行性和有效性。

1 基础知识

二元语义是基于符号转移值的概念提出来的，通常用二元组(si,α)来表示语言评价信息，si是语言术语集S={s0,s1, …,sg}中的元素，α为符号转换值并且α∈[-0.5, 0.5)。

定义1[1]设S={s0,s1, …,sg}为一个语言术语集，β∈[0,g]是语言术语经集结运算得到的实数，则与β对应的二元语义可通过函数Δ得到：

Δ: [0,g]→S×[-0.5, 0.5)

(1)

式中，round(·)表示通常的四舍五入取整运算。

定义2[1]设S={s0,s1, …,sg}为一个语言术语集，若(si,α)表示二元语义，则存在逆函数Δ-1将二元语义转换成相应的数值β∈[0,g]，即：

Δ-1:S×[-0.5, 0.5)→[0,g]

Δ-1(si,α)=i+α=β

(2)

为了定义犹豫二元语义元的可能度比较公式，本文首先给出两个二元语义间的二元关系。

定义3设S= {s0,s1, …,sg}为一个语言术语集，(si,αi)和(sj,αj)为任意的两个二元语义，二元关系p定义为：

(3)

2 犹豫二元语义术语集

定义4[3]设X为一论域，S={s0,s1, …,sg}为一个语言术语集，X上的一个犹豫语言术语集A可以表示为

A= {(x,h(x))|x∈X}

(4)

式中，h(x)= (si,αij)，x∈X。

犹豫二元语义表达模型利用一个二元组(si,αij)表达犹豫语言信息，其中，si为S上的一个语言术语，αij是[-0.5, 0.5)的一个有限子集，表示si可能的符号转移值。

称h(x)=(si,αij)为一个犹豫二元语义元，表示为h=(si,αij)={(si,ak)|k=1,2,…,l(h)}，h的上界为h+= max{ak|(si,ak)∈h}，下界为h-= min{ak|(si,ak)∈h}。

基于犹豫模糊语言可能度比较公式[13]的定义思想，本文将给出两个犹豫二元语义元大小的可能度比较公式。

定义5设h1=(si,αij)={(si,ak)|k=1,2,…,l(h1)}与h2=(sl,αlm)={(sl,bn)|n=1,2,…,l(h2)}是任意的两个犹豫二元语义元，则h1≥h2的可能度比较公式为：

P(h1≥h2)=

(5)

式中，(si,ak)∈h1，(sl,bn)∈h2，h1∩h2={(si,ak)|(si,ak)∈h1且(si,ak)∈h2}。

犹豫二元语义元的可能度比较公式具有如下性质。

1) 规范性：0≤P(h1≥h2)≤1。

3) 互补性：P(h1≥h2)+P(h2≥h1)=1。

4) 自反性：若h1=h2，则P(h1≥h2)=

P(h2≥h1)=0.5。

5) 传递性：若P(h1≥h2)≥0.5，P(h2≥h3)≥0.5，则P(h1≥h3)≥0.5。

证明易知定义5满足性质1)和5)，下面就性质2)～4)给出相应的证明。

(6)

(7)

3)P(h1≥h2)+P(h2≥h1)

(8)

4) 若h1=h2，则P(h1≥h2)=P(h2≥h1)。又P(h1≥h2)+P(h2≥h1)=1，则P(h1≥h2)=P(h2≥h1)=0.5。

定义6[3]设(si,αij)与(sl,αlm)是两个任意的犹豫二元语义元，且αij={ak|k=1, 2, …,l(αij)}，αlm={bn|n=1, 2, …,l(αlm)}，则(si,αij)和(sl,αlm)之间的距离被定义如下：

(9)

例2考虑例1中的犹豫二元语义元h1和h2，根据定义6可得h1和h2之间的距离为d(h1,h2) = 0+0.3=0.3。

3 基于ELECTRE的犹豫二元语义多属性群决策方法

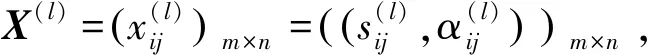
3.1 个体决策矩阵的集结

sij=

(10)

其中，算子的定义[3]为

表示通常的四舍五入运算，且：

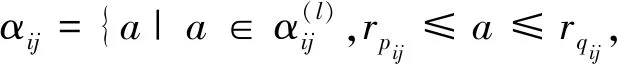
(11)

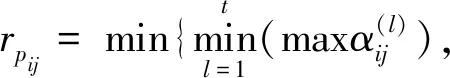
属性分为效益型属性和成本型属性，本文利用式(10)构建规范化犹豫二元语义群决策矩阵Y=(yij)m×n：

(12)

式中，neg(xij)可以根据式(13)确定。

neg(h)=

{Δ(g-(Δ-1(si,ak)))|k=1, 2, …,l(h)}

(13)

3.2 属性权重的确定

偏差最大化法是一种根据各属性下所有候选方案评价值之间的差异来确定属性权重的方法，差异越大的属性对决策的作用越大，其权重也就越大。计算第j(j=1, 2, …,n)个属性下所有候选方案间的总偏差为Vj：

(14)

式中，d(xij,xkj)表示候选方案Ai与Ak(i,k=1, 2, …,m;j=1, 2, …,n)在属性Cj下的距离。则第j(j=1, 2, …,n)个属性的权重为：

(15)

3.3 犹豫二元语义和谐性指数与不和谐性指数

(16)

(17)

(18)

传统ELECTRE法中的和谐指数Iik为：

(19)

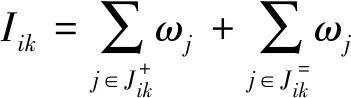
(20)

传统ELECTRE法中的和谐指数Iik是方案Ai不劣于方案Ak的那些属性的权重之和在所有属性权重的总和中所占的比例，没有考虑方案属性值之间的差异。因此，本文基于可能度比较公式定义犹豫二元语义和谐指数cik为方案Ai不劣于方案Ak的那些属性下可能度的加权之和，具体为：

(21)

式中，ωj(j=1,2,…,n)为属性Cj∈C的权重值，cik∈[0,1]表示方案Ai不劣于方案Ak的程度。cik越大，表示方案Ai不劣于方案Ak的程度越大。

不和谐性指数dik是指方案Ai与方案Ak在不和谐属性下的相对差异，它反映了候选方案之间的有限补偿。也就是说，当某个属性下的两个候选方案之间的差异达到一定程度时，决策者将拒绝其他属性下的收益对于该属性下的损失的补偿。不和谐性指数dik具体由式(22)确定。

(22)

式中，ωj(j=1, 2, …,n)为属性Cj的权重值。dik∈[0,1]能够反映方案Ai与方案Ak的相对劣势程度，并且dik越大，表示方案Ai劣于方案Ak的程度越大。

根据犹豫二元语义和谐性指数与不和谐性指数分别构建犹豫二元语义和谐性矩阵C=(cik)m×m与不和谐性矩阵D=(dik)m×m。

3.4 对候选方案排序

本文通过计算净优势值实现候选方案的排序。为此，需要根据犹豫二元语义和谐矩阵C及不和谐矩阵D的余矩阵D′=(1-dik)m×m的Hadamard乘积确定综合优势矩阵E=C∘D′=(eik)m×m，其中：

eik=cik(1-dik)

(23)

eik越大，表示方案Ai不劣于方案Ak(i=1, 2, …,m;j=1, 2, …,n)的程度越大。进一步的，根据式(24)确定方案Ai的净优势值：

(24)

式中，Ni越大，说明方案Ai越优。

将各方案的净优势值按照降序的顺序排列，就可以得到各方案由优到劣的排序。

3.5 决策步骤

基于以上分析，提出一种基于ELECTRE的犹豫二元语义多属性群决策方法。具体步骤如下：

Step1：根据3.1节集结决策者们的决策信息，得到群决策矩阵X=(xij)m×n(i=1, 2, …,m;j=1, 2,…,n)，并根据式(12)～(13)构建规范化犹豫二元语义群决策矩阵Y=(yij)m×n。

Step2：根据式(14)～(15)确定属性权重。

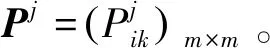
Step4：根据式(16)～(18)确定和谐集、不和谐集和无差异集。

Step5：构建和谐性矩阵C=(cik)m×m，其中，和谐指数cik由式(21)确定。

Step6：构建不和谐性矩阵D=(dik)m×m，其中，不和谐指数dik由式(22)确定。

Step7：根据式(23)构建综合优势矩阵E=(eik)m×m。

Step8：根据式(24)确定各方案的净优势值，并按降序排序，即净优势值越大的候选方案越优。

4 算例分析

本文所提方法的决策步骤如下。

Step1：根据3.1节确定的群决策矩阵X=(xij)5×4(i=1, 2, …, 5;j=1, 2, …, 4)，见表4。根据式(12)和式(13)构建的规范化群决策矩阵Y=(yij)5×4，见表5。

Step2：根据式(14)～(15)得到属性权重分别为ω1=0.2401，ω2=0.2234，ω3=0.2155，ω4=0.3210。

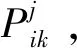
表1 犹豫二元语义决策矩阵X(1)

表2 犹豫二元语义决策矩阵X(2)

表3 犹豫二元语义决策矩阵X(3)

表4 犹豫二元语义群决策矩阵X

表5 规范化犹豫二元语义群决策矩阵Y

P2=

P3=

Step4：根据式(16)～(18)确定和谐集、不和谐集和无差异集，其中，“-”表示不存在使得方案Ai与Ak(i,k=1, 2, …, 5且k≠i)满足集合

Step5：构建和谐性矩阵C=(cik)5×5。

Step6：构建不和谐性矩阵D=(dik)5×5。

Step7：构建综合优势矩阵E=(eik)5×5。

Step8：根据式(22)分别计算净优势值，得到N1=-2.1434，N2=-0.5762，N3=-2.1946，N4=1.5189，N5=3.3953。根据净优势值越大，相应方案越优的排序原则有N5>N4>N2>N1>N3，则A5≻A4≻A2≻A1≻A3，故A5为最佳候选企业。

为了说明本文所提和谐指数的有效性，基于本文所提方法，按式(20)计算和谐指数，可得本文算例中各方案的净优势值依次为N1=-2.1793，N2=-0.5426，N3=-2.2562，N4=1.3521，N5=3.6260。比较分析见表6。由表6可知，基于两种和谐指数的排序结果是一致的，但利用式(21)计算和谐指数所得各方案的净优势值间差异比式(20)的略小，这主要是因为式(21)的和谐指数进一步考虑了方案两两比较的可能度信息。

此外，将本文所提方法与文献[3]、文献[14]的方法进行比较分析，结果见表7。由表7可知，三种方法的排序结果均为A5≻A4≻A2≻A1≻A3，最佳候选企业为A5，这说明本文所提方法是可行的。