关于伪Smarandache函数m次补数的一类均值

孙 忱，李江华

(西安理工大学理学院，陕西西安710054)

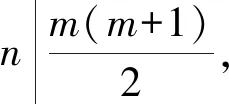
(1)

Z(n)的前几项数值分别为Z(1)=1，Z(2)=3，Z(3)=2，Z(4)=7，Z(5)=4，Z(6)=3，Z(7)=6，Z(8)=15，Z(9)=8，Z(10)=4，Z(11)=10，Z(12)=8，Z(13)=12，Z(14)=7，…。

伪Smarandache函数是David Gorski教授首次提出来的[1]。同时也研究了Z(n)的许多初等性质，并得到了一系列有意义的结果，例如：

1) 如果p≥3为一个素数，则Z(p)=p-1;

2) 如果n=2k，则Z(n)=2k+1-1;

3) 假设p是一个奇素数，则Z(2p)=p，如果p=3(mod4)；Z(2p)=p-1，如果p≡1(mod4)；

4) 对任意奇素数p,p|n且n≠p,有Z(n)≥p-1。

关于Z(n)的算数性质，许多学者也进行了研究，获得了不少有意义的结果。例如，冀永强[2]解决了Z(n)的上下界问题：

(2)

Lou[3]用初等和解析的方法证明了下面的结论：

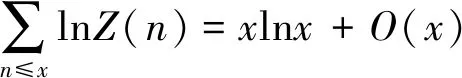
(3)

与此对应，所谓的Smarandache函数S(n)=min{k:n|k!}。Le[4]证明了如果n是一个完美数，则有如下等式成立：

S(n)=Z(n)

(4)

1)n=4p, 其中p≡1(mod8);

2)n=2kp(k>2), 其中p≡1(mod8)且p|(2k-2-1)。

文献[6]研究了伪Smarandache函数的一个混合均值问题，并给出了渐近公式：

(5)

这里P(n)是n的最大素因子,ai为可计算的常数。

事实上,Z(n)与P(n)之间有着非常密切的关系。所以对Z(n)函数与其最大素因子P(n)的研究非常必要。

本文受文献[7]的启发将利用初等和解析的方法研究Z(n)及其最大素因子在m次幂补数am(n)上的均值分布性质，并给出两个较强的渐近公式。式中ζ(m)表示Riemann zeta函数。

定理1对任意实数x>1，任意正整数m，有渐近公式：

(6)

定理2对任意实数x≥3，任意正整数m，有渐近公式：

(7)

1 几个引理

为了完成定理的证明，我们需要以下引理。

引理1[7]对任意素数p≥3和任意k∈N,有Z(pk)=pk-1。

引理2设k≥2是给定的整数，那么对任意充分大的正整数n，有:

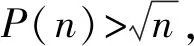
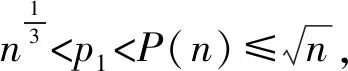
证明:

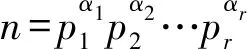
(8)

因此，根据Z(n)的初等性质有：

Z(am(n))=Z(Pm-1(n))=Pm-1(n)-1

(9)

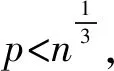
Z(am(n))=Z(Pm-1(n))=Pm-1(n)-1

(10)

引理3设m≥2是给定的整数，那么对任意实数x≥3有估计式：

(11)

证明:

根据Z(n)的初等性质，可得Z(n)≤2n-1。则有：

(12)

引理4设p为素数，其中k为正整数，则有估计式：

(13)

证明:

参阅文献[8]。

2 定理的证明

这节将完成两个定理的证明。

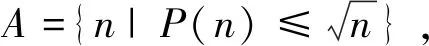
对任意正整数n>1，由Z(n)的初等性质和集合A的定义，则有：

(14)

故由上述引理1得：

(15)

对于集合B，我们根据Z(n)的定义和引理2的1)，有：

(16)

由Abel求和公式[9]有：

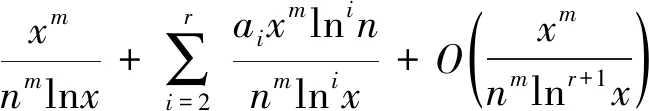
(17)

其中π(x)为x的素因子的个数。ai(i=2,3,…,r)是可计算的常数。

根据式(16)～(17)，我们有：

(18)

综上所述，结合式(14)～(18)有：

(19)

故定理1成立，接下来我们证明定理2。

Z(am(n))-Pm-1(n)+1=0。 故：

(20)

再根据引理3，可得：

(21)

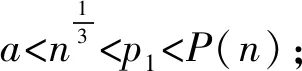
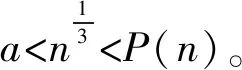
对于情形a)和b)中的n,显然，在这两种情况下有Z(am(n))-Pm-1(n)+1=0。故这两个和式分别为0。而对于c)中的n，当m≥3时，有:

Z(am(n))=Pm-2(n)-1

则有：

(22)

故结合式(20)～(22)及引理4，有：

(23)

于是完成了定理2的证明。